
- •Оглавление
- •Введение
- •1.1.2. Преобразование Фурье производной.
- •1.1.3. Преобразование Фурье убывающих функций.
- •1.1.4 Формула обращения преобразования Фурье
- •1.1.5. Преобразование Фурье в пространстве .
- •1.1.6. Преобразование Фурье функции нескольких переменных.
- •1.2. Мультипликаторы Фурье в пространстве
- •2.Пространство основных и обобщенных весовых функций.
- •2.1. Основные весовые функции. Весовые интегральные преобразования ,. Некоторые операции в пространстве
- •2.2 Весовое преобразование Фурье.
- •2.3. Класс весовых мультипликаторов .
- •3. Теорема существования и единственности решения дифференционального уравнения с переменными коэффициентами.
- •3.1. Постановка задачи
- •3.2. Теорема существования и единственности решения дифференциального уравнения с переменными коэффициентами.
- •3.3. Теорема оценки производных решения.
- •Литература
1.1.6. Преобразование Фурье функции нескольких переменных.
Пусть
теперь
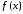 -функция
на
-функция
на -мерном
евклидовом пространстве
-мерном
евклидовом пространстве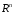 , причем
, причем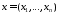 , где
, где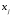 -координаты
точки в некоторой системе координат.
Функция
-координаты
точки в некоторой системе координат.
Функция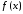 называется абсолютно интегрируемой,
если она интегрируема по любому шару
называется абсолютно интегрируемой,
если она интегрируема по любому шару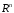 ,
, . Преобразование Фурье абсолютно
интегрируемой функции
. Преобразование Фурье абсолютно
интегрируемой функции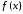 определяется формулой
определяется формулой
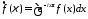 , 25125\* MERGEFORMAT (.)
, 25125\* MERGEFORMAT (.)
которая
по своему виду совпадает с формулой
14, но теперь
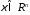 ,
,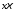 -означает
скалярное произведение, т.е.
-означает
скалярное произведение, т.е.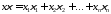 , где
, где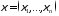 ,
знак интеграла, как мы уже говорили
выше, означает интегрирование по всему
,
знак интеграла, как мы уже говорили
выше, означает интегрирование по всему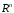 .
.
Преобразование
Фурье
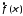 любой
любой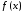 является непрерывной ограниченной
функцией и стремится к нулю при
является непрерывной ограниченной
функцией и стремится к нулю при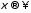 .
.
Если
функции
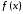 и
и абсолютно интегрируемы, то функция
абсолютно интегрируемы, то функция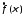 имеет непрерывную частную производную
имеет непрерывную частную производную и
и
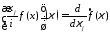 . 26126\* MERGEFORMAT (.)
. 26126\* MERGEFORMAT (.)
Доказательство этих утверждений получается почти дословно повторен соответствующих доказательств для одномерного случая.
Пусть
абсолютно интегрируемая функция
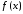 при всех
при всех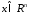 имеет частную производную
имеет частную производную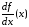 ,
которая является непрерывной и абсолютно
интегрируемой функцией. В таком случае
,
которая является непрерывной и абсолютно
интегрируемой функцией. В таком случае
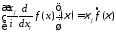 27127\* MERGEFORMAT (.)
27127\* MERGEFORMAT (.)
Доказательство
формулы 127 аналогично доказательству
формулы 111, поскольку
 -мернуы
интеграл
-мернуы
интеграл
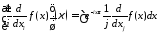
можно свести к повторному и тогда в интеграле по переменному можно будет произвести те же самые преобразования, которые были использованы при вводе формулы 111.
Определение
пространства
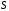 и сходящейся последовательности
и сходящейся последовательности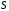 для функций многих переменных получается,
если индексы
для функций многих переменных получается,
если индексы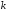 и
и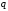 в приведенных выше определениях для
случая оного переменного заменить на
мультииндексы
в приведенных выше определениях для
случая оного переменного заменить на
мультииндексы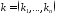 ,
,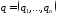 ,
считая, что
,
считая, что
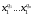 ,
,
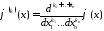 .
.
Если
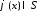 ,
то для любых
,
то для любых
 . 28128\* MERGEFORMAT (.)
. 28128\* MERGEFORMAT (.)
Действительно,
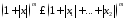 , а ограниченность функций
, а ограниченность функций устанавливается с помощью этого же
рассуждения, что и неравенство 128.
устанавливается с помощью этого же
рассуждения, что и неравенство 128.
Так
как
 -мерный
интеграл
-мерный
интеграл в том и только том случае, когда
в том и только том случае, когда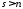 , то выбирая в 128 в качестве
, то выбирая в 128 в качестве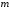 число
число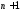 , получим, что функция
, получим, что функция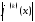 абсолютно суммируемы. В частности,
абсолютно суммируема и сама функция
абсолютно суммируемы. В частности,
абсолютно суммируема и сама функция .
.
Далее,
точно так же, как и в случае одного
переменного, доказывается, что для любой
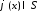 функция
функция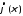 так же принадлежит
так же принадлежит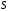 .
.
Для
функции
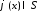 верна формула обращения преобразования
Фурье
верна формула обращения преобразования
Фурье
 .
.
Например, для случая функций от двух переменных
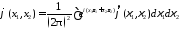 .
.
Действительно,
переходя от кратных интегралов к
повторным, переставляя порядки
интегрирования, что законно, так как
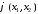 и
и абсолютно интегрируемы, и пользуясь
формулой обращения для функций одного
переменного, получим, что
абсолютно интегрируемы, и пользуясь
формулой обращения для функций одного
переменного, получим, что
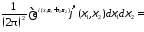
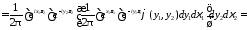
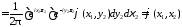
Аналогичным образов формула обращения доказывается в случае любого числа переменных. С помощью формулы обращения, как и в случае одного переменного, для функций многих переменнх устанавливается.
Теорема.
преобразование Фурье осуществляется
взаимно однозначное и взаимно непрерывное
отображение пространства
 на все
на все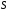 .
.
Отметим
еще, что для функций из
 справедлива формула
справедлива формула
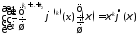 , 29129\* MERGEFORMAT (.)
, 29129\* MERGEFORMAT (.)
которая следует из 128.
1.2. Мультипликаторы Фурье в пространстве
Введем понятие мультипликатора[1].
Рассмотрим
функцию
 ,
пусть
,
пусть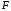 -
прямое преобразование Фурье, тогда если
-
прямое преобразование Фурье, тогда если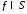 , то
, то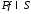
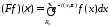 ,
где
,
где
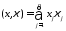 ,
,
и, следовательно, определено произведение:

По
определению функция
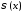 назевается мультипликатором в
назевается мультипликатором в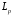
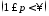 ,
если
,
если
1)
2)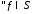 выполняется
выполняется
 , 30130\* MERGEFORMAT (.)
, 30130\* MERGEFORMAT (.)
где
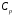 - константа, не зависимая от
- константа, не зависимая от , а
, а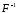 -обратное преобразование Фурье, т.е.
для
-обратное преобразование Фурье, т.е.
для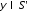 и
и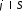
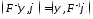 ,
где
,
где
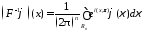 .
.
Возьмем
бесконечно дифференцируемые функции
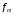 и функцию
и функцию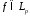 .
Пусть выполняется условие
.
Пусть выполняется условие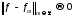 тогда из 130 следует, что
тогда из 130 следует, что
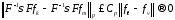 ,
при
,
при
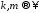 .
.
Из
последнего неравенстве следует, что
существует функция, к которой при
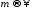 в смысле
в смысле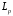 стремится
стремится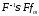 .
.
Можно
записать:
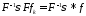 (данное равенство получается из теоремы
о преобразовании Фурье свертки
(данное равенство получается из теоремы
о преобразовании Фурье свертки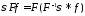 .
.
Очевидно
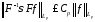 ,
,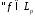
 ,
где
,
где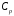 - та же констванта, что и в соответствующем
равенстве для
- та же констванта, что и в соответствующем
равенстве для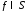 .
.
Множество
таких функций будем обозначать
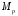 .
.
Зададим
вектор
 ,
где
,
где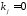 или
или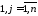 .
Носителем вектора
.
Носителем вектора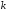 будем назвать множество
будем назвать множество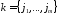 тех индексов
тех индексов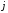 ,
для которых
,
для которых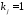 .
.
Теорема.
Пусть на
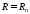 задана функция
задана функция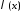 , обладающая свойствами: каков бы ни был
вектор
, обладающая свойствами: каков бы ни был
вектор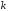 ,
производная
,
производная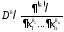 существует и неравенства в любой точке
существует и неравенства в любой точке ,
,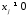 ,
где
,
где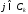 ,
и подчиняется неравенству
,
и подчиняется неравенству

Тогда
 - мультипликатор, т.е. существует
независимая от
- мультипликатор, т.е. существует
независимая от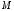 и
и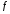 константа
константа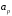 такая, что
такая, что
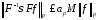 ,
,
 ,
,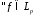 .
.
Заметим,
что т. к.
 удовлетворяет указанному в теореме
свойству и при
удовлетворяет указанному в теореме
свойству и при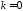 ,
то ограничена на
,
то ограничена на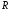 и непрерывна, разве что за исключением
точек, принадлежащих
и непрерывна, разве что за исключением
точек, принадлежащих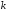 координатным плоскостям. Поэтому на
координатным плоскостям. Поэтому на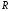 ,
, -
измеримая функция, и в то же время,
обобщенная.
-
измеримая функция, и в то же время,
обобщенная.
312Equation Section (Next)
