1.1.5. Преобразование Фурье в пространстве .

Дадим определение пространства , которое играет важную роль в ряде вопросов теории обобщенных функций. Функциябудем называть бесконечно дифференцируемой, если при всехсуществуют производные порядков. Так как из существования производнойвытекает непрерывность функции, считая, что по определению.

Совокупность всех бесконечно дифференцируемых функций обозначается через

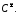
Определение. Совокупность всех бесконечно дифференцируемых функций , которые для всехудовлетворяют неравенствам

, 19119\* MERGEFORMAT (.)

где -постоянные, зависящие от функции, образует линейное пространство.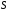

Оценки 119 показывают, что пространство , состоит из бесконечно дифференцируемых функций, убывающих на бесконечнсти вместе со всеми производными быстрее любой отрицательной степени.

Заметим, что вместо системы оценок 119 можно пользоваться эквивалентной системой

20120\* MERGEFORMAT (.)

где - некоторые другие постоянные, зависящие от выбора функции. Действительно, разлагая другие постоянные по формуле биномана сумму одночленов, получим, что левая часть в 13 есть сумма членов, каждый из которых в силу неравенства 119 ограничен. Тем самым доказано, что из 119 следует 120, что для всех

,

а функция интегрируема.

Наконец, если , то все функциитоже принадлежат. Отсюда, в частности, следует, что все функциитоже абсолютно интегрируемы.

Теорема. Преобразование Фурье взаимно однозначно отображает пространство на все.

Доказательство.

Так как для любой все функции тоже принадлежати, следовательно, абсолютно суммируемы, то в силу свойств преобразования Фурье, функциябесконечно дифференцируема. Покажем, что. Для этого достаточно доказать, что все функцииограничены, но это вытекает из того, что в силу формул 12 и 13.

, 21121\* MERGEFORMAT (.)

а функция тоже принадлежит, и следовательно, абсолютно интегрируема.

Остается вспомнить, что преобразование Фурье абсолютно интегрируемой функции ограничено.

Итак, если , то и. Обратное, пусть дана функция, покажем, что она является преобразованием Фурье некоторой функции. Положим, что.

Функция есть прямое преобразование Фурье функциии поэтому принадлежит. Но тогда, очевидно, и. По формуле обращения

поэтому есть преобразование Фурье функции.

Итак, мы проверили, преобразование Фурье отображает пространство на все.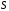

Это отображение взаимно однозначно, поскольку сама функция однозначно восстанавливается пос помощью формулы оращения.

Теорема доказана.

В пространстве можно ввести понятие сходимости последовательности.

Определение. Будем говорить, что последовательность функций изсходится в пространствек функциипри, еслиравномерно для всехи существуют такие константы, не зависящие оти от всех

. 22122\* MERGEFORMAT (.)

Теорема 2. Если 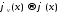в, то ив.

Доказательство. Будем опять использовать формулу 121. Из оценок 122 следует, что при некоторых выполнены неравенства

23123\* MERGEFORMAT (.)

поэтому из 121 получаем, что

.

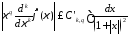Остается доказать, что равномерно для любых.

Так как

,

то достаточно проверить, что для любого

при24124\* MERGEFORMAT (.)

Из 122 следует, что

,

потому для любого можно найти такое, что, следовательно для любой

.

Так как равномерно, то, потому существует такое, что для всех

но тогда . Тем самым 124 доказано.

Утверждение теоремы 2 означает, что преобразование Фурье непрерывно отображает пространство в(отображение непрерывно, если оно всякую сходящуюся последовательность переводит в сходящуюся). Очевидно, что обратное преобразование Фурье тоже обладает этим свойством, поскольку оно связано с прямым преобразованием Фурье формулой 118.