Оглавление

Введение 2

1.Мультипликаторы Фурье 5

1.1. Преобразование Фурье 5

1.1.1. Определение преобразования Фурье 5

1.1.2. Преобразование Фурье производной. 11

1.1.3. Преобразование Фурье убывающих функций. 12

1.1.4 Формула обращения преобразования Фурье 14

1.1.5. Преобразование Фурье в пространстве . 18

1.1.6. Преобразование Фурье функции нескольких переменных. 25

1.2. Мультипликаторы Фурье в пространстве 30

2.Пространство основных и обобщенных весовых функций. 34

2.1. Основные весовые функции. Весовые интегральные преобразования , . Некоторые операции в пространстве 34

3. Теорема существования и единственности решения дифференционального уравнения с переменными коэффициентами. 48

3.1. Постановка задачи 48

3.2. Теорема существования и единственности решения дифференциального уравнения с переменными коэффициентами. 50

3.3. Теорема оценки производных решения. 52

Литература 55

Введение

В работе исседовано уравнение

, (1)

где ,

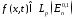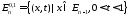
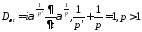
-постоянные комплексные коэффициенты;

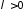- параметр;

-весовая функция 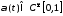, удовлетворяющая условиям:

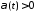при ;

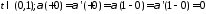Работа состоит из трех папаграфов.

В первом параграфе приводятся основные понятия и опрделения, исседуемые в дальнейшем.

Во втором параграфе изучены пространства основных и обобщенных функций, весовое преобразование Фурье, весовые мультипликаторы.

В третьем параграфе рассматривается уравнение (1). Наряду с пространствами Соболева используются пространства Соболева-Слободецского.

Доказаны теоремы существования единственного решения при выполнении некоторого дополнительного условия.

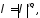
Теорема 1. Пусть выполнено условие 1 и 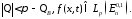Тогда при любом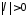существует единственное решение, для которых справедлива оценка:

.

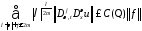Теорема 2 оценки производных решения.

Пусть .

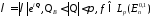Тогда при 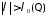выполняются следующие оценки:

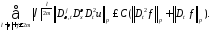
11Equation Section (Next)

1. Мультипликаторы Фурье

   1. . Преобразование Фурье

1. .1. Определение преобразования Фурье

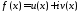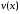Пусть на всех задана функция. принимающая комплексные значения, гдеи- функции с вещественными значениями. Для любого отрезкаинтеграл отопределяется по формуле:

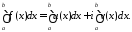212\* MERGEFORMAT (.)

Таким образом, интегрируемость функции 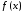по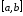равносильна одновременной интегрируемости по этому отрезку функцийи. Аналогично определяются и несобственные интегралы от функций с комплексными знамениями.

Определение. Функция 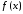называется абсолютно интегрируемой, если она интегрируема на любом конечном отрезке и

, 313\* MERGEFORMAT (.)

_{то есть несобственный интеграл от} по всей оси _{сходится.}

_{Будем обозначать - несобственный интеграл по всей оси.}

_{Определение. Преобразованием Фурье абсолютно интегрируемой функции называется функцияпеременной, которая определяется по формуле [1]:}

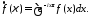414\* MERGEFORMAT (.)

Пример. Вычислим преобразование Фурье функции

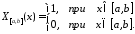
Если в 14 вместо 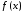подставить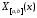, то получим:

515\* MERGEFORMAT (.)

Для любого комплексного числа справедлива формула Эйлера:

. 616\* MERGEFORMAT (.)

_{Используя формулы Эйлера, легко убедиться, что функция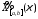} при всех _{и стремится к нулю при .}

_{Поскольку при любых вещественных значениях x и}

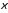
, 717\* MERGEFORMAT (.)

_{то для любой абсолютно интегрируемой функции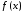} интеграл в 14 сходится при всех 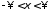_и

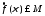, где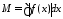. 818\* MERGEFORMAT (.)

Таким образом, функция определена при вещественных значениях и ограничена.

1.1.2. Лемма 1. Преобразование Фурье любой абсолютно интегрируемой функцииявляется непрерывной ограниченной и стремится к нулю при.

Доказательство. Прежде всего заметим, что утверждение выполнено для любых ступенчатых функций. Действительно, функция 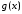называется ступенчатой, если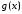вне некоторого отрезкаи существует такое разбиение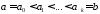отрезка, что на каждом интервале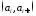функция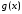постоянна.

В таком случа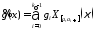е , где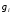- значение функций на интервале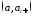, а для отдельных слагаемых этой суммы утверждение леммы уже проверили выше.

Для любой абсолютно интегрируемой функции 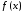можно найти такую последовательностьступенчатых функций, что

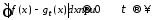. 919\* MERGEFORMAT (.)

Действительно, достаточно показать, что для любого 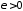можно найти такую ступенчатую функцию,

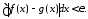10110\* MERGEFORMAT (.)

Поскольку интеграл от по всей оси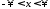сходится, то существуют такие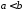, что

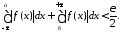
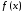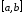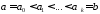Так как предполагаем, что интегрируема по Риману на, то в силу критерияотрезка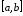, что

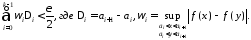
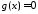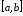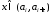Чтобы построить ступенчатую функцию , для некоторой выполняется. Теперь достаточно положитьвсе отрезкаипри, где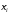- некоторая фиксированная точка из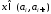. При этом не имеет существенного значения как именно определяетсяв самих точках.

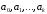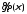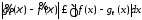После того, как последовательность , ступенчатых функций, удовлетворяющих 15 для доказательства утверждения леммы остается заметить, что последовательностьравномерно сходится к, поскольку, и воспользоваться свойствами равномерно сходящихся последовательностей.