Для студентов / Лекции / (2)ВЕД / (5)Рівняння електростатики і магнітостатики

5. Рівняння електростатики і магнітостатики

У цьому розділі ми розглянемо явний вигляд диференціальних та інтегральних рівнянь електростатики і магнітостатики. Більш конкретно, спираючись на результати розділу 3, ми побудуємо диференціальні рівняння типу

,

які задають розбіжності електричного і магнітного полів, а також міри їх завихреності. У згоді з розділом 1, це буде саме та інформація, яка дозволяє відтворити структуру полів в областях їх існування. Застосовуючи теореми Гауса-Остроградського і теорему Стокса, ми перейдемо також від диференціальних до інтегральних рівнянь електричного і магнітного полів.

а) Рівняння електростатики

Згідно (3.9) і (4.3), значення потенціалу і напруженості електричного поля, утвореного зарядом, розподіленим з густиною в області , визначаються формулами:

, . (5.1)

За визначенням,

, (5.2)

де - позначає оператор Лапласу. Застосуємо його до першого з рівнянь (5.1):

. (5.3)

В розділі … було встановлено (див.()), що

.

Підставляючи це рівняння в формулу (5.3) і використовуючи властивості дельта-функції, отримуємо:

. (5.4)

Це диференціальне рівняння для скалярного потенціалу є відомим як рівняння Пуассона. Порівнюючи його з (5.2), можемо надати йому вигляд:

, (5.5)

який розшукується нами згідно постановки задачі. Друге розшукуване диференціальне рівняння електростатики

(5.6)

є тривіальним і віддзеркалює потенціальний характер електричного поля, прямо зафіксований другою з формул (5.1).

Як бачимо, диференціальні рівняння електростатичного поля (5.5) і (5.6), а також рівняння Пуассона (5.4) для потенціалу узгоджуються з принципом локальності. Крім того, вихідне інтегральне рівняння для потенціалу (5.1) отримано за допомогою принципу суперпозиції.

Інтегруючи ліву і праву частини рівняння (5.5) по об’єму і застосовуючи до інтегралу в лівій частині теорему Гауса-Остроградського, отримаємо наступний інтегральний аналог (5.5):

. (5.7)

Тут є поверхня, яка охоплює об’єм . Інтегральне рівняння (5.7) прийнято називати законом Гауса-Остроградського. Так само, інтегруючи ліву і праву частини рівняння (5.6) по довільній поверхні, яка спирається на замкнутий контур , і застосовуючи до інтегралу в лівій частині теорему Стокса, отримаємо наступний інтегральний аналог (5.6):

. (5.8)

б) Рівняння магнітостатики

Тут вихідним є рівняння (4.4) для векторного потенціалу:

. (5.9)

У згоді з його означенням (див. (3.11)), напруженість магнітного поля дорівнює:

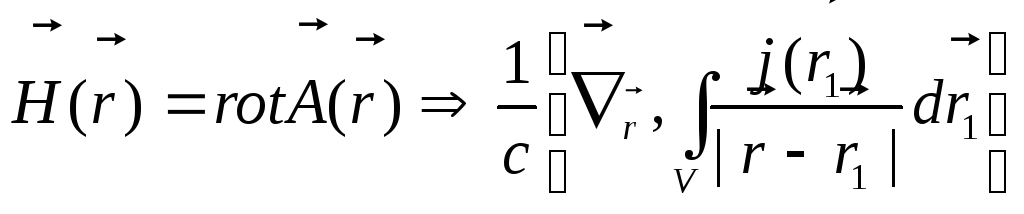. (5.10)

Оскільки оператор набла діє на змінну , по якій інтегрування не виконується, його можна внести під знак інтегралу. Тут має місце наступна послідовність перетворень:

.

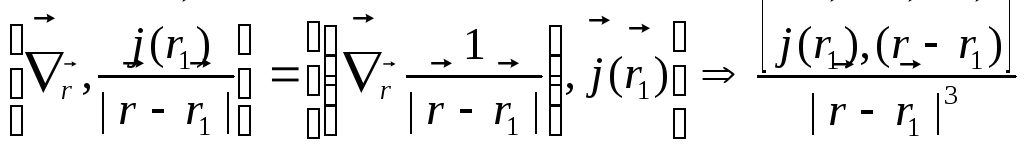Остаточно, для напруженості магнітного поля, утвореного током, розподіленим з густиною по об’єму , отримуємо:

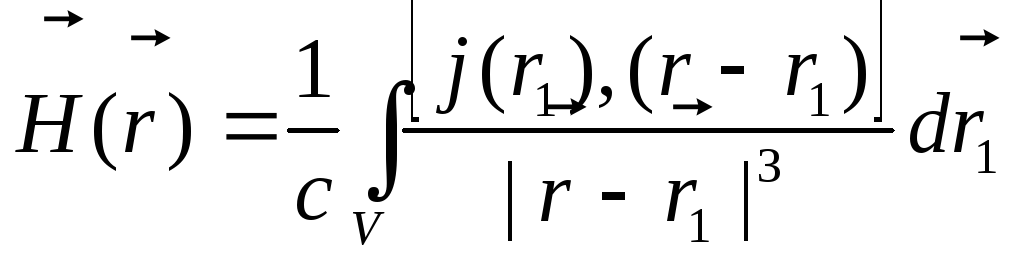. (5.11)

Перше з основних диференціальних рівнянь магнітостатики є тривіальним:

. (5.12)

Воно безпосередньо випливає з формули (5.10), яка явно засвідчує вихровий характер магнітного поля. Зазначимо, що воно було отримано в розділі 3 (див. (3.16)) з інших позицій. Для отримання другого з рівнянь, застосуємо до (5.10) операцію обчислення ротора:

.

Розкриваючи подвійний векторний добуток за стандартним правилом (див.()) , знаходимо:

.

Дія оператора Лапласа на векторний потенціал розраховується у такий самий спосіб, як і у випадку скалярного потенціалу (див. (5.3) і (5.4)):

. (5.13)

Тепер перейдемо до обчислення дивергенції від векторного потенціалу. Застосуємо оператор до лівої і правої частин (5.7):

. (5.14)

Скористаємось тепер перетворенням, відомим як перетворення Лежандра:

. (5.15)

Розрахуємо внесок першого доданку (5.15) в об’ємний інтеграл (5.14). За допомогою теореми Гауса-Остроградського об’ємний інтеграл перетворюється в поверхневий:

.

Поверхневий інтеграл занулюється внаслідок того, що нормальна складова току через поверхню , яка охоплює об’єм , дорівнює нулю. Далі, приймемо до уваги те, що лінії току в об’ємі є замкнутими (в статичній задачі ніде не відбувається накопичення зарядів). Це призводить до того, що

, (5.16)

і внесок другого додатку (5.15) в об’ємний інтеграл (5.14) також зануляється.

Таким чином, для статичного магнітного поля

(5.17)

а ротор його напруженості задовольняє рівнянню:

. (5.18)

Диференціальні рівняння (5.12) і (5.18) утворюють основу магнітостатики. Вони, як і рівняння Пуассона (5.13) для векторного потенціалу, узгоджуються з принципами суперпозиції і локальності.

Якщо в області виконуються рівняння

(5.19)

то магнітне поле в ній можна описувати також за допомогою скалярного «потенціалу» . Приймається, що . З першого з рівнянь (5.19)

зразу ж випливає, що

, (5.20)

тобто «магнітний потенціал» за відсутності токів в області задовольняю такому ж самому рівнянню Лапласа, як і електричний потенціал за відсутності в області електричних зарядів. Але подібність рівнянь не означає еквівалентності їх розв’язків. Нижче ми покажемо, що задовольняє зовсім іншим граничним умовам. Крім того, введення «магнітного потенціалу» є можливим тільки в обмеженій області простору.

Інтегральні аналоги цих рівнянь мають наступний вигляд:

(5.21)

і

, (5.22)

де - довільна поверхня, яка спирається на контур . Формула (5.22) отримана за допомогою теореми Стокса. Якщо контур охоплює лінійний струм, то інтеграл дорівнює величині струму і формула (5.22) переходить у

. (5.23)

В теорії електромагнітних явищ формула (5.23) вперше була побудована Біо і Саваром. На їх честь її і називають інтегральною теоремою Біо-Савара.

Якщо контур охоплює лінійних струмів, то формула (5.23) узагальнюється очевидним чином:

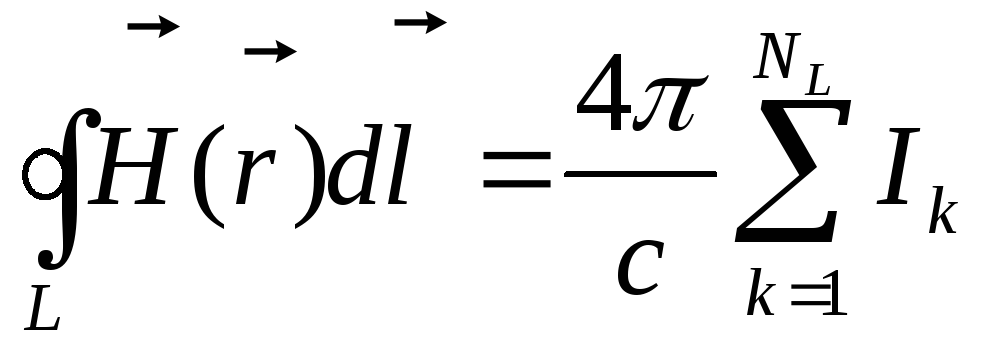
Розв’язуючи диференціальні рівняння електростатики і магнітостатики, ми можемо встановити структуру електричного і магнітного полів. Але для їх однозначного визначення потрібно задовольнити граничним умовам на поверхні, яка охоплює область існування полів, а також на всіх можливих внутрішніх поверхнях. Ця проблема буде повністю досліджена після побудови рівнянь Максвела.