Для студентов / Лекции / (2)ВЕД / (21)Частотная зСвойства электромагнитного поля осциллятора Герца

Частотная зависисимость электромагнитного поля осциллятора Герца.

Согласно определению осциллятора Герца, радиус-вектор подвижного заряда изменяется по гармоническому закону:

.

Это значит, что

,

и

, ,

Для многих целей более удобным является комплексное экспоненциальное представление:

,

в котором

.

В этом случае

, .

Конечно, физический смысл имеют только действительные части радиуса-вектора , дипольного момента , его производных и других физических величин. Поэтому, оперируя с комплексными величинами, на последнем этапе мы будем отделять их действительные части. Этот подход не приводит ни к каким затруднениям, пока мы осуществляем линейные операции над комплексными векторами. Но при определенных оговорках и ограничениях он может применяться и тогда, когда над векторами производятся нелинейные операции.

С использованием комплексного представления для напряженностей полей и находим:

,

Учитывая, что частота и длина волны связаны соотношением: , можно написать:

Отсюда следует, что характерные области поведения электромагнитного поля задаются неравенствами:

1. Квазистатическая зона:

2. Индуктивная зона:

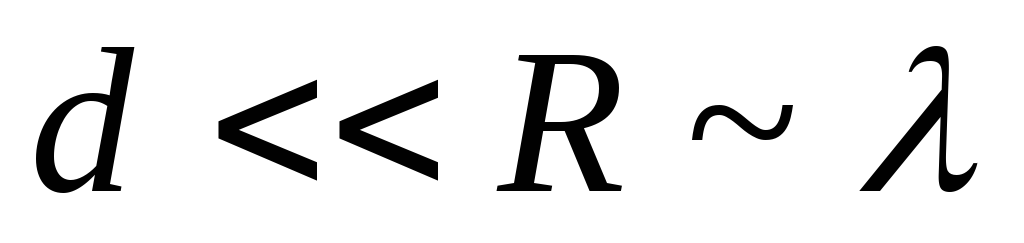
3. Зона излучения:

Поле излучения системы зарядов.

Рассмотрим поле излучения системы зарядов на большом расстоянии от нее: .

Благодаря неравенству , можно воспользоваться дипольным приближением. Каждый из зарядов излучает по закону:

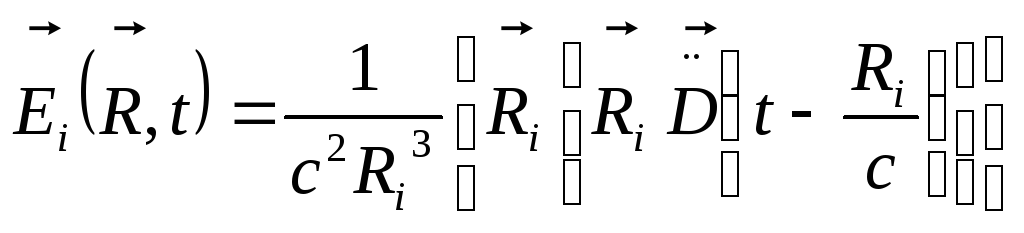
где . Фактически мы можем анализировать только одну из величин или , так они связаны соотношениями

= - или =.

Упростим это выражение, воспользовавшись тем, что

Имеем:

Поэтому:

Вклад величины мал по сравнению с единицей:

и им, очевидно, можно пренебречь. Точно также, вектор

по величине и направлению практически не отличается от вектора . В то же время, малая поправка во временной комбинации существенна.

Это сразу становится ясным при анализе частотной зависимости . Действительно, предполагая, что все заряды, включая ый заряд, колеблются по гармоническому закону , находим:

Последний множитель можно переписать в виде , где волной вектор излучаемой волны (- единичный вектор, задающий направление на точку наблюдения). По порядку величины и, в общем случае, не мало, если размер системы больше или сравним с длиной волны. Иными словами, множитель неодинаковость фаз излучения, создаваемых каждым из зарядов, и позволяет, таким образом, учесть интерференционные эффекты.

Фактически мы можем анализировать только одну из напряженностей или , так как они связаны между собою соотношением:

или

С учетом этого, мы находим, что напряженность магнитного поля, созданного системой на частоте , равна:

Так как - ая компонента дипольного момента, то

,

Отсюда следует, что

,

СВОЙСТВА ПОЛЯ ИЗЛУЧЕНИЯ

Уравнения электромагнитного поля:

1. 

2. 

3. 

4. 

Э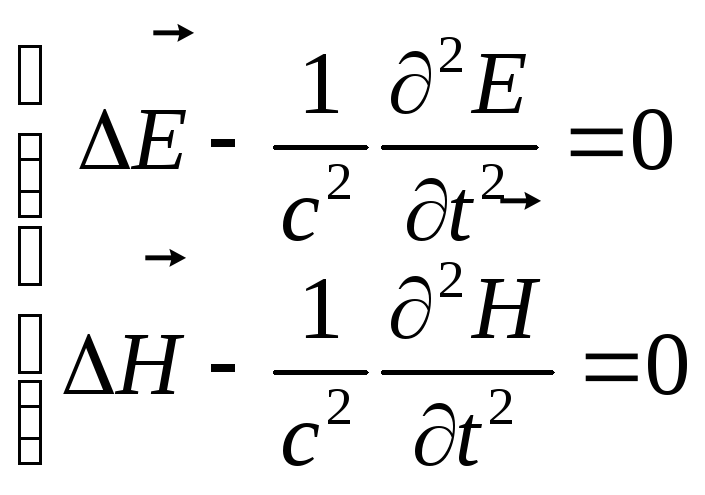 та система уравнений эквивалента двум волновым уравнениям:

Плосковолновое решение:

-

это электромагнитное возмущение, в котором значения и зависят только от одной линейной переменной.

Более точно: