Диференціальне числення ФБЗ

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Одесский национальный университет им. И.И. Мечникова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

= 600 , l = b =

.pdf

Скачиваний:

Добавлен:

20.05.2015

Размер:

813.81 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 86 7 8 > Следующая >>>

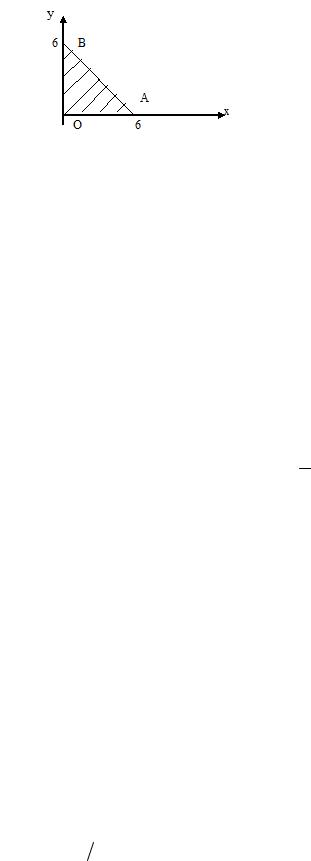
! D , ! + ( " x = 0, y = 0, x + y = 6 ( . 13).

$ . 13.

2 ( 6 . / ,:

u′	= xy (4 − 3x − 2 y ), u′	= x2 (2 − x − 2 y ) .
x	y

'' " ' xy x2 (

OAB x ≠ 0, y ≠ 0 ), " *:

4 − 3x − 2 y = 0,

2 − x − 2 y = 0.

2 , : x = 1, y = 1 . # , ,

" + * OAB . 2 "

0 1,

( : f 1,

' + OAB . $" "

OA , x = 0

y = 0 , " 6

OA OB ,

u (O ) = u ( A) = u (B ) = 0 . $"

AB . <

" "

y = 6 − x , u = ϕ( x) = x2 (6 − x)(2 − x − 6 + x) = −4x2 (6 − x),

0 ≤ x ≤ 6 .

ϕ′(x) = −48x + 12x2 = 0 , x = 0 ,

= 4 . &

[0, 6]

+ * x2 = 4 . 2 " ϕ( x ) ( ϕ(4) = −128 .

ϕ(0) = ϕ(6) = 0 .

) + (! *6 " u = x2 y (2 − x − y )

+ G

', 1 4 , ( 6 −128 .

2. % , ! ABCD

S ( . 14). 5 ! l , b , α , ! "

! ( 6 '?

; " ! ( 6 ', " ( 6 ' !

u = AB + BC + CD = 2l + b .

/ ,:

S = BC + AD EC . 2

$ . 14.

) * EC = l sin α , BC = b , AD = BC + 2 ED = b + 2l cos α ,

S = b + b + 2l cos α l sin α = (b + l cos α)l sin α . 2

b =

− l cos α .

l sin α

u = f (α,l ) =

2l +

− l cos α = l

(2 − cos α) +

l sin α

2 . 14 , 0 < α <

, 0 < l < +∞ . #

f (α ,l )

( 6

9 "

f (α,l )

( ,

G = 0 < α <

, 0

< l < +∞

6 " , * 0 < sin α < 1, 0 < cos α < 1 0 < α < π . 2

2 (:

f ′	= l sin α −	S cos α	,	f ′ = 2 − cos α −		S	.

α		l sin 2 α		l	l	2 sin α

8 ' * + G . 2 ( ,

f ′	,	f ′	'' * ':
α		l
			l	2	sin	3	α − S cos α = 0,
			l		sin		α − S cos α = 0,
			2 sin α (2 − cos α) − S = 0.
		l	2 sin α (2 − cos α) − S = 0.

2 " " , : l 2 =	S	.

	(2 − cos α )sin α
	(2 − cos α )sin α

% "' 6 " ", ( α :

S sin2 α − S cos α = 0, sin2 α − 2 cos α + cos2 α = 0, 2 − cos α

1 − 2 cos α = 0, cos α = 1 , α = π .

l =		S				=	2 S
									.
			π		π		4
		− cos	π		π		4	27
	2			sin
	2			sin
			3		3
											π		2
7 ",											π		2		S	" f (α , l )
										α =		, l =
											3		4
														27
														27

" , ( 6 " (! * (). # , 6 :

20./ .

! * (! *6 ( 6 " "

* " + " ( * , " , +, ’" "

6 ". 2, ' , ( + "

(! *6 ( 6 * ( ! + (

+ ( ' * " , + * (

+). 2 + + * ! , * "' * "

" ". # , ( ( .

. ( ( + G n f1( x),..., fm ( x) ,

m < n . .( E – + + G , * "' *

" *:

f1( x) = 0,..., fm ( x) = 0 .		(20.1)
$" " (20.1) ! " " ’".
. # x0 = ( x	,..., x	) E , * "
01	0n

( ) f0 ( x) " ’" (20.1), " ,

( Sδ ( x0 ) , " x E ∩ Sδ ( x0 ), x ≠ x0 : f0 ( x) > f0 ( x0 )

( f0 ( x) < f0 ( x0 )) .

# ' * "

%, (20.1) + "-! * m

xk 6 . #, 6 * xk

6 n − m , , ' F n − m . 0

, + " ( (!) F , " + * n − m .

. 2 ( u = 1 − x2 − y2 , "

x + y = 1.

$" " ’" x + y = 1 ’" , * " y : y = 1 − x . % ( ' u :

u = 1 − x2 − (1 − x)2 = 2 x − 2 x2 .

# ( ( ,

u = F ( x) = 2 x − 2 x2 . 7 ",, " " ,

x = 1 2 . 5 x = 1 2 , y = 1 2 . # (1 2 ,1 2) , '

u = 1 − x2 − y2 " ’" x + y = 1,

umax = u(1 2 ,1 2) = 1 2 .

* ’" (20.1)

, * " +, " + "

6 , * " 6 ( , # ( #. $" ' n + m :

L( x, λ) = f0 ( x) + λ1 f1( x) + ... + λm fm ( x) ,

x G , λ = (λ1,..., λm ) m . 4 λ1,..., λm ' * " #

( #, " L( x, λ) – " ( #.

. # ( x0 , λ0 ) n+m , * "

" & ( #, "

∂L( x0 , λ0 )	= 0,...,	∂L( x0 , λ0 )		= 0 ,
∂x1		∂xn

∂L( x0 , λ0 )	= f ( x0 ) = 0,...,		∂L( x0 , λ0 )		= f		( x0 ) = 0 .
						m
∂λ1	1			∂λm

		∂f ( x0 )
		1
		∂x1
		∂x1
A =		L

	∂fm ( x0 )

		∂x1
		∂x1

		∂f ( x0 )
L	1
L		∂xn
		∂xn
L L			.

L	∂fm ( x0 )

		∂xn
		∂xn

	2		n n	∂2 L(x0 , λ0 )
d		L( x0	, λ0 ) = ∑ ∑		dx dx
	xx
					j k
			j =1 k =1	∂x j∂xk

(! 2- " L( x, λ) ( x0 , λ0 ) , " ( ! ' 6 x1,...xn , + ' λ1,..., λm .

∂f j ( x

)

= dx = (dx

,..., dx ) :

∑ dx2

> 0,

∑

dx = 0,

j = 1, m .

k =1

∂xk

( ). * ! " &

f1( x),..., fm ( x) x0 n 2-

, rang A = m , ! ( x0 , λ0 ) n+m

" & ( # L( x, λ) .

+, d xx2 L( x0 , λ0 ) > 0 dx ET , x0

" & f0 ( x) ’ (20.1). d xx2 L( x0 , λ0 ) < 0

dx ET , x0 " & f0 ( x)

’ (20.1). dx ET " d xx2 L( x0 , λ0 ) #

, ! ’ , x0

’ (20.1).

" .

1. 2 ( u = x − 2 y + 2z

x2 + y2 + z2 = 1 .

' 7 +:

L( x, y, z, λ) = x − 2 y + 2z + λ( x2 + y2 + z 2 − 1) .

2 ( 7 +, " ’"+

" *:

∂L

= 1 + 2λx = 0,

∂L

= −2 + 2λy = 0 ,

∂x

∂y

∂L

= 2 + 2λz = 0,

∂L

= x2 + y2 + z2 − 1 = 0 .

∂z

∂λ

2 6 * " * ,:

x = −

, y =

, z = −

2λ

% "' " ", ,:

= 1,

4λ2

λ2

λ1 = − 3 2,

λ2 = 3 2 . # " 7 + ,

2 2

1 2

2 3

, −

, M

2 −

, −

3 3 3 2

2-( 7 + x, y, z . / ,:

∂2 L

= 2λ,

∂2 L

= 0,

∂2 L

= 0 ,

∂x2

∂x∂y

∂x∂z

∂2 L

= 0,

∂2 L

= 2λ,

∂2 L

= 0 ,

∂y∂x

∂y2

∂y∂z

∂2 L

= 0,

∂2 L

= 0,

∂2 L

= 2λ .

∂z∂x

∂z∂y

∂z2

# :

d 2 L = 2λ(dx2 + dy2 + dz 2 ) .

" M

,: d

2 L(M

) = −3(dx2

+ dy2 + dz2 ) , " M

2 L(M

) = 3(dx2 + dy2 + dz2 ) . ) + dx2 + dy2 + dz2 > 0 ,:

d 2 L(M1) < 0 , d 2 L(M 2 ) > 0 . # (1 3, − 23, 23) –

, (−1 3, 23, −23) – .

2. 2 9, , " * A

", B , 6 ', * " (, " + " "

! . % ', A B 6

, ', 6 * 6 " 6 ', v1 , – v2 ,

" .

. ( t1 – + " 6 , t2 – . # ( . 15):

$ . 15.

t1 =	a		=	b
		, t2			.

	v1 cos α1			v2 cos α2

# , ! ':

T (α1, α2 ) = t1	+ t2 =			a		+		b

			v1 cos α1				v2 cos α2
			v1 cos α1				v2 cos α2
,
a tg α1 + b tg α2 = l .
' 7 +:
L(α1, α2 , λ) =		a		+		b		+ λ(l	− a tg α1 − b tg α2 )

		v1 cos α1			v2 cos α2
		v1 cos α1			v2 cos α2

( :

∂L

a sin α1

−

λa

= 0,

∂α1

v1 cos

α1

cos

α1

∂L

b sin α2

−

λb

= 0,

∂α2

v2 cos2

α2

cos2

α2

∂L

= a tg α + b tg α

− l = 0.

∂λ

λ =

sin α1

sin α2

(20.2)

2 ( ( 7 + α1, α2 :

sin α1

d 2 L =

+ 2a

− λ

dα12 +

v1 cos α1

cos2 α1

sin α2

+ 2b

− λ d α22 .

v2 cos α2

cos2 α2

& (20.2) ( ,:

d 2 L =

dα2 +

dα2

> 0 .

v1 cos α1

v2 cos α2

) + " T , ( , " , * " *: sin α1 = sin α2 .

v1 v2

8 ( , " .

2 ( " ! + * , *

6. # " * , * ", (

" + ", * 6 *. / + 7 + , ! * ", , ,

! + " ' * " ' (. &

+ 7 + ' * '. &

' * " ’", – !,

21. "

& .

% * + * ,

! * * * + *

, y 6 x . 2 * ( " +, " , , * " , ( , * "

! , " , . 0 " ,

, ! ! + , ' *

* .

. ( * m * y

" x :

x	x1	x2	L	xm
y	y1	y2	L	ym

2 * ( " * + y = f ( x) + x

y ', * " *, ! 6 "

( ( x1, y1 ), ( x2 , y2 ),..., ( xm , ym ) . .(, ,

6 , " . 16.

$ . 16.

# ' y = f ( x) + ( ': y = ax + b . % *

a,b , . .( 6 , "

. 17.

$ . 17.
# ' y = f ( x) + ':	y = axb . %
a,b + , .
%, " y = f ( x) + * n
a1, a2 ,..., an , ! , ":
y = f ( x, a1, a2 ,..., an ) .	(21.1)

. 6 ' ' ! , ! "

(21.1) " + " * ,

!. % 6 ’" " , ,

!$ . % " , . $" '

S (a1, a2 ,..., an ) = ∑ ( yk − f ( xk , a1, a2 ,..., an ))2 .

k =1

8" " ! * ! + +

* " yk y , " ! (21.1). % a1, a2 ,..., an ! ' * "

, ! " S (a1, a2 ,..., an ) ! ( 6 ". 2 (

– * *

* , ! ( 6 '.

# , + "

S (a1, a2 ,..., an ) .

. ! " a1, a2 ,..., an

* " " *:

∂S	= 0,	∂S	= 0,...,	∂S	= 0 .	(21.2)

∂a1		∂a2		∂an

! ":

<<< < Предыдущая 1 2 3 4 56 / 86 7 8 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.05.2025144.9 Кб0ДИПЛОМНА Марінов.doc
#
20.05.2015278.02 Кб17Дипломна работа Маша Станкова 4-болг332.doc
#
01.05.2025286.21 Кб0дипломна робота текст.doc
#
01.03.2025648.7 Кб0Дипломна робота.doc
#
01.04.20251.6 Mб0Диущак Юля.doc
#
20.05.2015813.81 Кб6Диференціальне числення ФБЗ.pdf
#
20.05.20151.08 Mб9Диференціальне числення ФОЗ.pdf
#
20.05.2015237.57 Кб11ДифференцПсихолЛекции.doc
#
20.05.2015983.01 Кб245Длекции с картинками.docx
#
12.11.2019259.07 Кб2Для 3 курсу _ПС.doc(3 перших заняття).doc
#
01.05.2025114.69 Кб0Для бакалавров.doc