
Диференціальне числення ФБЗ
.pdf
|
z′ |
|
= 2x − y , z′ = −x + 2 y , z′ (M ) = z′ (M ) = 1 . |
|||||
|
x |
|
|
|
y |
x |
y |
|
2 ( " l : |
||||||||
|
|
|
|
|
|
|
|
|
|
l |
= 36 + 64 = 10; |
cosα = 0, 6; |
cos β = 0,8 . |
||||
|
|
|
|
|
|
|
|
|
# : |
|
|
||||||
|
∂z |
|
|
= 1 0, 6 + 1 0, 8 = 1, 4 . |
|
|||
|
|
|
|
|||||
|
|
|
|
|
|
|||
|
∂l |
|
|
|
||||
|
|
M |
u = x2 − 2xz + y2 A(1; 2; −1) |
|||||
|
|
|||||||
2. |
|
2 ( |
||||||
" A B (2; 4; − 3) .
2 ( l = AB ( " : l = AB = {1; 2; − 2} = i + 2 j − 2k , l = 
 1 + 4 + 4 = 3,
1 + 4 + 4 = 3,
cosα = |
1 |
, |
cos β = |
2 |
, |
cos γ = − |
2 |
. |
|
|
|
||||||
3 |
|
3 |
|
3 |
|
|||
2 ( " A :
∂u |
|
|
= (2x − 2 z ) |
|
x =1 |
|
|
|
|
||||
|
|
|
|
|
||
∂x |
|
|
||||
|
A |
|
|
z =−1 |
||
|
||||||
= 4 |
, |
∂u |
|
|
= 2 y |
|
y =2 = 4 , |
∂u |
|
|
= −2 x |
|
x =1 |
= −2 . |
||
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
∂y |
|
A |
∂z |
|
A |
|||||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
# ' (3) ,:
|
∂u |
|
|
|
|
|
|
|
1 |
|
2 |
|
|
2 |
16 |
|
|
|
|
||
|
|
|
|
= |
|
4 |
|
+ 4 |
|
− 2 |
− |
|
= |
|
|
. |
|
|
|
||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
∂l |
|
A |
|
|
3 |
|
3 |
|
|
3 |
3 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||||||||||
) * |
∂u |
|
|
> 0 , 6 " " ,. |
|
||||||||||||||||
|
|
|
|||||||||||||||||||
∂l |
|
||||||||||||||||||||
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3. 2 ( u = e− xy M ( x , y |
) |
x2 + y2 = R2 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
||
" ( . |
|
|
|
||||||||||||||||||
& n |
|
, ! , " |
|||||||||||||||||||
( x0 , y0 ) , , , {x0 , y0 } |
– , |
||||||||||||||||||||
" ( , " ( ( ( . 8).
$ . 8.
32
. " n '' *:
cos α = |
|
x0 |
, cosβ = |
y0 |
. |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
: |
|
|
|
|
R |
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
∂u |
|
|
|
= − y e− x0 y0 , |
∂u |
|
|
|
|
|
= −x e− x0 y0 . |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
∂x |
|
|
|
|
|
|
|
|
0 |
|
|
∂y |
|
|
|
|
|
|
|
|
0 |
|
|
|
|||||||
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
#: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
∂u |
|
|
|
|
= |
∂u |
|
|
|
cos α + |
∂u |
|
|
cos β = |
|
|
|||||||||||||||
|
∂n |
|
M |
|
∂x |
|
M |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
∂y |
|
M |
2x y |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
= − y e |
− x y |
|
x |
|
− x e |
− x y |
|
y |
= − |
|
− x y |
|||||||||||||||||||||
|
0 0 |
|
|
0 |
|
|
0 0 |
|
0 |
|
0 0 |
|
e |
0 0 . |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
0 |
|
|
|
|
|
|
|
R |
|
|
|
0 |
|
|
|
R |
|
|
|
|
R |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
&, " "
, ! * .
14. % '.
$" u = f ( x, y, z) M ( x0 , y0 , z0 ) "
" l :
|
∂u |
|
|
|
= |
∂u |
|
|
|
cos α + |
∂u |
|
|
|
cosβ + |
∂u |
|
|
|
|
|
cos γ . |
|
|
|
|
(14.1) |
|||||||||||
|
∂l |
|
|
∂x |
∂y |
∂z |
|
|
|
|
||||||||||||||||||||||||||||
|
|
M |
|
|
M |
|
|
M |
|
|
|
M |
|
|
|
|
|
|
|
∂u |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
% ": " ! " l , ! |
|
( " |
||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||
∂l |
||||||||||||||||||||||||||||||||||||||
(! *6 "? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
2 (14.1) ,, |
∂u |
|
|
|
+ " " " ( |
|||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||
∂l |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂u |
|
|
|
∂u |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
! : |
∂u |
|
|
, |
|
|
, |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂x |
M |
|
∂y |
|
|
|
∂z |
|
|
M |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
||||||||||||
l = {cos α, cosβ, cos γ} .
|
|
|
|
|
|
|
∂u |
|
|
|
∂u |
|
|
|
∂u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
. & |
|
|
, |
|
|
, |
|
|
, * " |
||||||||||
|
∂x |
|
∂y |
|
|
∂z |
|||||||||||||
|
|
|
|
|
|
|
M |
|
|
|
|
M |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
u = f ( x, y, z) M . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
% , * " , " |
|
|
|
|
|
|
|
|
|
||||||||||
uuuuuur uuur |
|
∂u |
|
∂u |
|
∂u |
|
|
|
|
|
|
|
|
|
|
|
|
|
grad u = u = |
, |
, |
. |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
∂x |
∂y |
|
∂z |
|
|
|
|
|
|
|
|
|
|||||
# :
33

∂u |
|
|
uuuuuur |
|
|
r |
|
|
|
||||||
|
|
= (grad u |
|
|
, l ). |
||
|
|
|
|
|
M |
||
∂l |
|
M |
|||||
|
|
|
|||||
|
|
|
|
|
|||
|
|
|
|
|
|||
2 " " ! ,:
∂u |
|
= |
|
uuuuuur |
|
|
|
r |
cos ϕ , |
||
|
|||||||||||
|
|
|
|||||||||
|
|
grad u |
|
|
l |
||||||
|
|
|
|
|
|
||||||
∂l |
M |
M |
|||||||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
ϕ – + , l ( . 9).
$ . 9.
) * cos2 α + cos2 β + cos2 γ = 1, |
|
r |
|
= 1 , +: |
||||||||||||
|
|
|||||||||||||||
|
l |
|
||||||||||||||
|
∂u |
|
= |
|
uuuuuur |
|
cos ϕ , |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
grad u |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
∂l |
M |
M |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
! " l |
|
M ', + |
||||||||||||||
, " l . ), |
∂u |
|
( , * |
|||||||||||||
|
||||||||||||||||
∂l |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
" cos ϕ = 1 , ! ϕ = 0 , ,, " l *
! , * " " , u . % *:
|
∂u |
|
∂u |
|
uuur |
|
|
|
∂u |
2 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|||||||
max |
= |
= |
u |
|
= |
|
|||||
|
|
|
|
|
|
|
|||||
∂l |
∂( u) |
|
|
||||||||
l |
|
|
|
|
|
|
∂x |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
∂u 2 |
|
∂u 2 |
||
+ |
|
|
+ |
|
. |
|
|
||||
|
∂y |
|
∂z |
||
. * + +, , ,
" * 6 " (*
∂u |
|
uuur |
|
> 0 ) . ) , " (6 6 |
|
|
|
||||
= |
u |
|
|||
|
|
||||
∂( u) |
|||||
|
|
|
|
||
|
|
|
|
" ! , * " " −grad u , !
.
, * " , n u = f ( x1 , x2 ,..., xn ) :
34

uuuuuur uuur |
∂u |
|
∂u |
|
∂u |
|
grad u = u = |
|
, |
|
,..., |
|
. |
|
|
|
||||
|
∂x1 |
|
∂x2 |
|
∂xn |
|
" 2- u = f ( x, y) :
uuuuuur |
|
|
|
|
|
|
∂u |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|||||
|
|
∂u |
|
|
|
|
|
||
grad u |
|
= |
|
|
|
, |
|
|
. |
|
∂x |
|
|
∂y |
|||||
|
M |
|
|
M |
|
|
|
||
|
|
||||||||
|
|
|
|
|
|
|
|
|
M |
. , " , 2- ,
" " , . (, ( x, y) a
f ( x, y) = C , |
∂u |
, − |
∂u |
. ) + " ( |
||||||||
|
|
|||||||||||
|
|
|
|
|
|
|
|
∂y ∂x |
||||
! |
|
|
|
|
|
|
|
|
|
|
|
|
r uuur |
∂u |
|
∂u |
|
∂u |
|
∂u |
|
|
|
|
|
(a, u ) = |
|
|
|
− |
|
|
|
= 0 , |
|
|
|
|
∂y |
∂x |
∂x |
∂y |
|
|
|
|
|||||
,, u " ( a , !
" ( ' f ( x, y) = C .
.
1. 2 ( " , u = xyz M (2,1,1) . / ,:
|
∂u |
|
|
= yz |
|
= 1, |
∂u |
|
|
= xz |
|
= 2, |
∂u |
|
|
= xy |
|
= 2 . |
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||
|
∂x |
|
|
|
|
|
|
|
|
M |
∂y |
|
|
|
|
M |
∂z |
|
|
|
|
M |
|||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
M |
|
|
|
|
|
|
|
|
|
|
M |
|
|
M |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
# : |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
uuuuuur |
|
= {1, 2, 2} . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
grad u |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
+ ,: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
uuuuuur |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
grad u |
|
M |
= 1 + 4 + 4 = 3 . |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
. " , , * " ( " :
cos α = |
1 |
, cos β = |
2 |
, cos γ = |
2 |
. |
|
|
|
||||
3 |
3 |
3 |
|
|||
2. ' * " " "
h = 20 − x2 − y 2 .
4
% ! , " ' * h = 20 , 19 , 18 , 16 11 . ." grad h , " ( 6 , (
– * . % ! grad h M (2,1) .
35
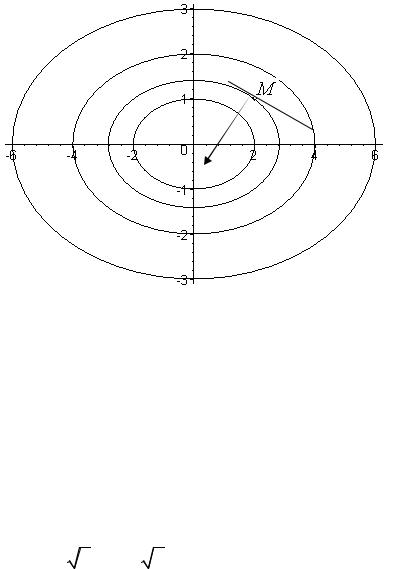
$ . 10. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
% ! , ( . 10): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
1) |
|
h = 20 ; |
|
x2 |
|
+ y 2 = 0 – (0, 0); |
|
|
|
|
||||||||||||||||||||||
4 |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2) |
|
h = 19 ; |
x2 |
|
+ y2 = 1 – " a = 2 , b = 1; |
|
||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3) |
|
h = 18 ; |
|
|
|
|
x2 |
+ y 2 = 2 , |
! |
|
x2 |
|
+ |
|
y 2 |
= 1 – |
|
" |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
4 |
|
|
|
|
8 |
|
2 |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a = 2 2 , b = |
2 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
4) |
|
h = 16 ; |
|
|
|
|
x2 |
+ y 2 = 4 , |
! |
x2 |
|
+ |
|
y 2 |
|
= 1 |
– |
|
|
" |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
4 |
|
|
|
|
16 |
|
4 |
|
|
|
|
|
|
|
|||||||||||
a = 4 , b = 2 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
5) |
|
h = 11; |
|
|
|
|
x2 |
+ y 2 = 9 , |
! |
|
x2 |
+ |
y 2 |
|
= 1 |
– |
|
|
" |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
4 |
|
|
|
|
36 |
|
9 |
|
|
|
|
|
|
|
|||||||||||
a = 6, |
b = 3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
# M (2,1) + * |
" ( ) |
h = 18 . |
, |
|||||||||||||||||||||||||||||
" ( " (, " (
" ( ( . 10). 2 (:
|
∂h |
|
|
|
x |
|
|
|
∂h |
|
|
||
|
|
|
= − |
|
|
= −1, |
|
= − 2 y |
= −2 , |
||||
|
|
|
|
|
|
|
|||||||
|
∂x |
|
M |
2 |
|
|
M |
∂y |
|
|
M |
||
|
|
|
|
|
|
||||||||
|
|
|
|
|
M |
||||||||
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||
+ |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
36 |
|
|

uuuuuur |
|
= {−1; − 2}, |
|
uuuuuur |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
= 1 + 4 = 5 . |
|||||||
grad h |
|
|
grad h |
|
|
||||||
|
|
M |
|
|
|
M |
|
|
|
|
|
|
|
|
|||||||||
|
15. + . |
||||||||||
$" 3 |
' P , " " ": |
||||||||||
F ( x, y, z) = 0 . |
(15.1) |
||||||||||
. % " " , * " P
M ( x0 , y0 , z0 ) P , " , ' "-! * , " + *
P * M ( . 11).
$ . 11.
) * M * ! , + *
P , ( , " * M , !,
+, !.
. 5 M ( x0 , y0 , z0 ) P ∂F  ∂x, ∂F
∂x, ∂F  ∂y,
∂y,
∂F ∂z ' *, , ! ",
∂z ' *, , ! ",
M , * " ! ' P . 5 M !
,, ! ( '' * ', M
, * " ' P .
. M ( x0 , y0 , z0 ) |
! P , |
P M # ! . |
|
. $" P " ' L , " * |
|
M . .( L " ": |
|
x = ϕ(t), y = ψ(t), z = χ(t) . |
(15.2) |
37

r
# r (t) = {ϕ(t), ψ(t), χ(t)} – - * (
L . 2, " x0 = ϕ(t0 ), |
y0 = ψ(t0 ), z0 = χ(t0 ) , r (t0 ) – - |
||||||||||||||||||||||||
M ( x0 , y0 , z0 ) . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
& |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
r |
|
|
|
d ϕ(t) d ψ(t) d χ(t) |
|
|
||||||||||||||||||
|
dr (t) |
= |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
, |
|
|
|
|
, |
|
|
|
|
|
|
|
|
|||||
|
dt |
|
|
dt |
|
|
|
dt |
|
|
|
dt |
|
|
|
||||||||||
, L * ( , . 2 |
|||||||||||||||||||||||||
|
r |
|
) |
|
dϕ(t |
|
|
) d ψ(t |
|
|
) dχ(t |
|
) |
||||||||||||
|
dr (t |
0 |
|
0 |
0 |
0 |
|||||||||||||||||||
|
|
|
= |
|
|
|
, |
|
|
|
|
, |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
dt |
|
|
|
|
dt |
|
|
|
|
|
|
dt |
|
|
|
|
|
dt |
|
|
|
|||
– ( L M ( x0 , y0 , z0 ) .
5 (15.2) " " (15.1), ,
+ * t , * L + * P :
|
F (ϕ(t), ψ(t), χ(t)) ≡ 0 . |
|
|
|
|
|
|
|
|
|
|
(15.3) |
|||||||||||||||||||||||||||||||||||
2 ', ' + * t : |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
∂F |
|
|
|
dϕ(t) |
+ |
∂F |
|
dψ(t) |
+ |
∂F |
|
dχ(t) |
≡ 0 . |
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂z |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
∂x |
dt |
|
|
|
∂y |
|
|
dt |
|
|
dt |
|
|
|
|
|
||||||||||||||||||||||||||||||
2, ' * " M : |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
∂F |
|
|
|
d ϕ(t0 ) |
+ |
∂F |
|
|
|
|
|
|
|
d ψ(t0 ) |
+ |
∂F |
|
|
|
|
d χ(t0 ) |
= 0 . |
|
|
||||||||||||||||||||||
|
∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂z |
|
|||||||||||||||||||||||
|
|
M |
|
|
|
|
dt |
|
|
|
|
|
|
∂y |
|
|
M |
|
dt |
|
|
|
|
M |
|
dt |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
∂F |
|
|
|
|
|
|
|
|
∂F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
& |
|
∂F |
|
|
|
, |
|
, |
|
|
, , u = F ( x, y, z) M . |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
∂x |
|
M |
|
|
∂y |
|
|
|
|
|
|
|
|
∂z |
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
# " ( ! * M |
|||||||||||||||||||||||||||||||||||||||||||||||
', ': |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
uuuuuur |
|
|
|
|
|
|
r |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
dr (t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
grad F |
|
|
, |
|
0 |
|
|
|
= 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
uuuuuur |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dr (t0 ) |
|
|||||||||||
) + grad F |
|
|
|
|
|
" ( |
. % |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
" " ! *-" L , " + * P
* M . ) + ( ! *-"
uuuuuur
" ( ( + grad F . # , "
M
P M + * ( , *
r uuuuuur
" , N = grad F . # .
M
. %, " ( 6 "
P , " " * M , , * "
P M ( . 12).
38
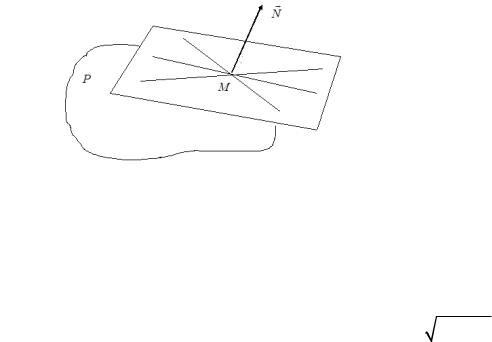
$ . 12.
5 M – ( P , (
!’" ,. ! +
. " ( + * + (
. . , 6 z = 
 x2 + y2 , ! '
x2 + y2 , ! '
'. ( + * (
( '' * ').
' * " " 3 , " *
M ( x0 , y0 , z0 ) , * ( N = { A, B,C} :
A( x − x0 ) + B( y − y0 ) + C ( z − z0 ) = 0 ,
, , " ,
|
uur |
|
|
uuuuuur |
|
|
|
|
|
∂F |
|
|
|
|
∂F |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
∂F |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
N = grad F |
|
= |
|
|
|
|
|
|
, |
|
|
|
|
, |
|
|
|
|
|
|
, |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
M ∂x |
M |
|
∂y |
|
|
|
|
∂z |
M |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
||||||
+ " " P M : |
||||||||||||||||||||||||||||
|
∂F |
|
|
( x − x ) + |
∂F |
|
|
|
( y − y |
) + |
∂F |
|
|
( z − z |
) = 0 . |
(15.4) |
||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
∂x |
|
|
0 |
|
∂y |
|
|
|
|
|
|
0 |
|
|
|
∂z |
|
|
0 |
|
|
||||||
|
|
M |
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
M |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
5, , " " z = f ( x, y) , " "
! , ":
z − z |
|
= |
∂f (x0 , y0 ) |
(x − x ) + |
∂f (x0 , y0 ) |
( y − y ) . |
(15.5) |
0 |
|
|
|||||
|
|
∂x |
0 |
∂y |
0 |
|
|
|
|
|
|
|
|
||
. % " ", " M ( x0 , y0 , z0 ) |
|
||||||
P " ( , , * " .
' * " " " 3 , "
* M ( x0 , y0 , z0 ) , " ( {m, n, k} :
39

x − x0 = y − y0 = z − z0 , m n k
+ , " ,
uur uuuuuur |
|
|
|
, + " " : |
|
|||||||||||||
|
|
|
|
|||||||||||||||
N = grad F |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
x − |
x0 |
= |
y − |
y0 |
= |
z − |
z0 |
. |
(15.6) |
||||||||
|
|
|
|
|
|
|
||||||||||||
|
|
∂F |
|
|
|
|
|
|
∂F |
|
|
|
|
∂F |
|
|
|
|
|
|
∂x |
|
|
|
|
|
|
|
|
|
∂z |
|
|
|
|||
|
|
M |
|
|
|
∂y |
|
M |
|
|
M |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5, , " " " z = f ( x, y) , " "
! , ":
x − x0 |
= |
y − y0 |
= |
z − z0 |
. |
fx′(x0 , y0 ) |
f y′(x0 , y0 ) |
|
|||
|
|
−1 |
|||
! ". .( " F ( x, y, z) = 0 , ' " " "
3- u( x, y, z) , !
F ( x, y, z) = u( x, y, z) − C = 0 .
# , ", " ( *
M ( x0 , y0 , z0 ) , , |
uur uuuuuur |
|
|
uuuuuur |
|
. # " , |
|
|
|||||
N = grad F |
|
|
= grad u |
|
||
|
|
|
M |
|
|
M |
|
|
|
|
|
u( x, y, z) M , " "
u( x, y, z) , " * M .
. 2 ( " " , "
" ":
3xy2 − 2 yz + 4xz − 4 = 0 |
(15.7) |
M ( x0 , y0 , z0 ) , " x0 = −1, y0 > 0, |
z0 = −2 . |
) * M + * ,
* " " " (15.7). 2 (
:
3 (−1) y02 − 2 y0 (−2) + 4 (−1) (−2) − 4 = 0 .
2, ' y0 > 0 , ,: y0 = 2 ,
M (−1, 2, −2) – . 2 (:
uuuuuur |
|
|
|
|
|
∂F |
|
|
|
∂F |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
∂F |
|
|
|
|
|
|
|
|
|
|
|||
grad F |
= |
|
|
|
, |
|
|
|
, |
|
|
|
|
= |
∂x |
|
|
∂y |
|
|
∂z |
||||||||
|
M |
|
M |
|
|
|
|
|
|
M |
|
|||
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
= {(3y2 + 4z) |
|
, (6xy − 2z) |
|
M |
, (−2 y + 4x) |
|
M |
} = {4, −8, −8}. |
|
|
|
||||||
|
|
M |
|
|
|
|
||
|
|
|
|
|
|
|
|
" * + " ( , ! (
(, ! *6 ( n = {1, −2, −2} . ) + " "
, (15.4), , ":
(x + 1) − 2( y − 2) − 2( z + 2) = 0 ,
" " , (15.6):
40

x + 1 = y − 2 = z + 2 . |
||
1 |
−2 |
−2 |
16. ( + .
$" ' 2- u = f ( x, y) . .( ' *
u′ |
= |
f ′( x, y), u′ |
= |
f ′( x, y) . 8 * |
|
x |
|
x |
y |
|
y |
+ , " x, y , ( + + ! '
x y ((, "). # ! + (
(u′ )′ , (u′ )′ |
|
, (u′ )′ |
, (u′ )′ |
. 8 ' * " |
||||||||||||||||||||||||||||||||||||||||
x x |
|
|
x y |
|
y x |
|
|
|
y |
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2- u = f ( x, y) |
' * " ": |
|||||||||||||||||||||||||||||||||||||||||||
(u′ )′ |
|
= |
|
|
∂ |
|
|
∂u |
= u′′ |
|
= |
∂ |
2u |
|
, |
|
|
(u′ )′ = |
|
∂ ∂u |
= u′′ = |
|
∂2u |
, |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
x |
x |
|
|
∂x |
|
|
|
|
xx |
|
|
∂x2 |
|
|
|
|
|
|
x |
y |
|
|
|
|
|
|
xy |
|
∂x∂y |
|
||||||||||||||
|
|
|
|
|
∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂y |
∂x |
|
|
|
|
||||||||||||||||||
(u′ )′ |
|
= |
∂ |
|
∂u |
= u′′ |
= |
∂2u |
, |
(u′ )′ |
= |
∂ |
|
∂u |
|
= u′′ |
= |
∂2u |
. |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
y |
x |
|
|
|
|
|
|
|
|
yx |
|
|
|
∂y∂x |
|
|
y y |
|
|
|
|
∂y |
yy |
|
|
∂y 2 |
|
|||||||||||||||||
|
|
|
|
|
∂x |
∂y |
|
|
|
|
|
|
|
|
|
|
|
|
∂y |
|
|
|
|
|
||||||||||||||||||||
% u′′ , u′′ ' * " $ . |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
xy |
yx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
' * " 2- " n |
||||||||||||||||||||||||||||||||||||||||||||
u = f ( x1 , x2 ,..., xn ) : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
u′′ |
|
= (u′ |
)′ |
|
|
|
|
∂2u |
|
|
|
|
|
|
∂ |
|
|
|
|
∂u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
= |
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
x j xk |
|
|
|
|
x j |
xk |
|
|
∂x |
∂x |
|
|
|
|
∂x |
|
∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
k |
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
. 2 ( 2- " |
||||||||||||||||||||||||||||||||||||||||||||
u = 5x3 − 4x2 y + 8xy2 − 3 y3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
2 ( 1- ": |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
u′ = 15x2 − 8xy + 8 y2 , u′ = −4x2 + 16xy − 9 y2 . |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2- ": |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
u′′ |
= 30 x − 8 y |
, u′′ |
|
= −8x + 16 y , u′′ |
|
= −8x + 16 y , u′′ = 16x − 18 y . |
||||||||||||||||||||||||||||||||||||||
xx |
|
|
|
|
|
|
|
|
|
|
|
|
xy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yx |
|
|
|
|
|
|
|
|
|
|
yy |
|
||||
/ !, u′′ |
, u′′ |
|
. & , ? 4 + |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xy |
|
|
yx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
! * ' 6 , ! + *
" ' "? & * ,
.
,3 ( $ ). "
u = f ( x, y) |
& u′ |
, u′ |
, u′′ |
, u′′ |
|
|||||
|
|
|
|
|
x |
y |
xy |
yx |
|
|
( x , y |
) , u′′ |
, u′′ |
|
( x , y |
) , ! |
|||||
|
0 |
0 |
xy |
yx |
|
0 |
0 |
|
|
|
# : |
|
|
|
|
|
|
|
|||
u′′ |
= u′′ . |
|
|
|
|
|
|
|
|
|
xy |
yx |
|
|
|
|
|
|
|
|
|
3 ; (1843–1921) – * ( .
41
