Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Одесский национальный университет им. И.И. Мечникова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Диференціальне числення ФБЗ

.pdf

Скачиваний:

Добавлен:

20.05.2015

Размер:

813.81 Кб

Скачать

☆

<<< < Предыдущая 12 / 82 3 4 5 6 7 8 > Следующая >>>

$" ' 2- z = f ( x, y) .

$ . 4.

. ( z = f ( x, y) , * " +

Oxy , " " " ! , ( + ", !

+ , " * "' * * f ( x, y) = C , C –

7 " " z = f ( x, y) , 6, " " Oxy

P , " , z = f ( x, y) , '

z = C ( . 5).

$ . 5.

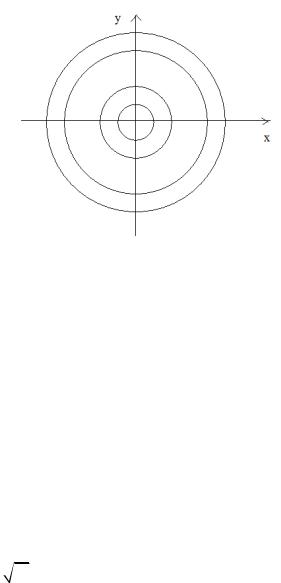
. 7 " " z = x2 + y2 ,

(0,0). + , ' C . 2 ' C = 0 , (0,0) ( . 6).

$ . 6.

7 " 2- " * ", ,

. 8 , " ’" ' * (

. . , ’" ' * '

' ", ’" ' * '

', ! – .

" " + " * ! *6

. " 3- u = f ( x, y, z) , * "

+ 3 , " " " ! , ( + ", ! " * "' * * f ( x, y, z) = C , C – .

., " u = x2 + y2 + z2 " " ,

C (0, 0,0) . " ( ! *6 "

' +.

6. % .

$" ' n u = f ( x1 , x2 ,..., xn ) . %, "

" " D x0 = ( x10 ,..., xn 0 ) n

" x0 .

. 4 A , * " " & u = f ( x1 , x2 ,..., xn )

x → x0 , " ε > 0 δ > 0 , x D, ρ( x, x0 ) < δ : | f ( x1 , x2 ,..., xn ) − A | < ε .

/ + " ( (

(" ():

. 4 A , * " " & u = f ( x1 , x2 ,..., xn )

x → x0 , " " ! * " {xk } , "

+ * D , , lim xk = x0 , : lim f ( xk ) = A .

k → ∞ k → ∞

3 * * * " +, " ( "

, .

5 A , ' u = f ( x) x → x0 , 6:

lim f (x) = A .

x→ x0

$", , ' 2- z = f ( x, y) . .( ' '

" D ( x0 , y0 ) " ( x0 , y0 ) . 5 A , ' z = f ( x, y) ( x, y) → ( x0 , y0 ) , 6:

lim f ( x, y) = A .

x→ x0 y→ y0

# ! ε > 0 δ > 0 : ( x, y) D , 0 < ( x − x )2	+ ( y − y )2	< δ :
0	0
\| f ( x, y) − A \| < ε .

1. , lim( x2 + y2 ) = 10 . 2 * ε > 0

x→ 3 y→1

| f ( x, y) − A |=| x2 + y2 − 10 | = | ( x − 3)2 + 6( x − 3) + ( y − 1)2 + 2( y − 1) | ≤ ≤| x − 3 |2 +6 | x − 3 | + | y −1|2 +2 | y −1| .

2 , " , ! " ! * " x, y ,

( x − 3)2 + ( y − 1)2 < δ , ! | x2 + y2 − 10 | < ε , *, !

δ2 + 6δ + 2δ = δ2 + 8δ < ε , ! 0 < δ < 16 + ε − 4 . . , + "

δ= 4 + ε4 − 2 . # , " * ε > 0 (6 δ > 0 ,

( x − 3)2 + ( y − 1)2 < δ

| x2 + y2 − 10 | < ε . 8 ( ,, lim( x2 + y2 ) = 10 .

x→ 3 y→1

2. , "

f (x, y) =

2xy

x2 + y2

, ( x, y) → (0, 0) . & * *

( xk

, yk ) =

. ) * k f

( xk , yk ) = 1 ,

lim f ( xk , yk ) = 1 . #

k → ∞

* * ( x′

, y′ ) =

, −

. # k

f ( x′

, y′ ) = −1, +

lim f ( x′		, y′ ) = −1 . " ! * " k	( x	, y	k	) , ( x′	, y′ )	' *
k → ∞	k	k	k		k	k	k
k → ∞
' (0,0) , {( xk , yk )} , {( xk′ , yk′ )}								" ' *

(0,0) . # 6 * , " ' *

" , " ' * *. 8 ,,

" f ( x, y) , ( x, y) → (0, 0) .

. 9 " u = f ( x) , " " x0 (' ' x0 ) n , * "

x0 , " , lim f (x) , lim f ( x) = f ( x0 ) .

x→ x0 x→ x0

# !, " ε > 0 δ > 0 , x S

( x0 )

| f ( x) − f ( x0 ) | < ε .

. ( x0 = ( x ,..., x

) , x = ( x ,..., x

) . %: x

= x

− x

(k =

1, n

0 n

0 k

u = f ( x) − f ( x0 ) . .

–

u – " & x0 . ), , "

x → x0 ,

x → 0

(k =

), "

f ( x) → f ( x0 ) ,

u → 0 . #

1, n

" x0 + ' .

. 9 " u = f ( x) , " " x0 (' ' x0 ) n , * "

x0 , " lim u = 0 .

x1 →0

...

xn →0

# ! x0 ,

( ( ( .

3. % +, " u = x2 + y2 ! * " (

Oxy . .( ( x0 , y0 ) – * Oxy . 9 "

u = x2 + y2 ( Oxy , f ( x , y				) = x2		+ y2	. 7
		0	0		0	0
( 1), lim ( x2 + y2 ) = ( x2					+ y2 ) . ) + "
		x→ x0		0		0
		x→ x0
		y→ y0
( x0 , y0 ) .
4. 9 "
	2xy	, x ≠ 0, y ≠ 0,


f ( x, y) = x2 + y2
	0, x = 0, y = 0
	0, x = 0, y = 0

, ' (0,0), * , x → 0, y → 0 , ( . 2).

7 , " u = f ( x) , u = g ( x) x0 ,

u = f ( x) ± g ( x) , u = f ( x) g ( x) + x0 . 4 u = f ( x) g ( x) x0 , " g ( x0 ) ≠ 0 .

. 9 " u = f ( x) , * " # G ,

" " " + ( + G .

& # ' &. " u = f ( x)

! # ! # G , " u = f ( x) #

# G .

# ' &. " u = f ( x)

! # ! # G , " u = f ( x)

# G !$ !$ .

7. ( . $" ' u = f ( x1 , x2 ,...xn ) , " " D

M ( x , x ,...x ) n . . (		x	x "
1 2	n	1	1

M ′( x1 + x1 , x2 ,...xn ) , " + + , 6 * ' ' + D .

$6 M 6 , * " '.

. ) u = f ( x1 , x2 ,...xn ) M

' x1 , * "

x1 u = f ( x1 + x1, x2 ,...xn ) − f ( x1, x2 ,...xn ) .

. 5 , " lim	x1u	, " "

x1 → 0	x1

, * " 1- " & u = f ( x1 , x2 ,...xn )

x1 , , * " "

∂u	=	∂f	= f ′	( x , x ,...x ) .

∂x1			x	1 2	n
		∂x1
		1

' * " u = f ( x1 , x2 ,...xn )

M + ' 6 x1 , x2 ,...xn :

x j u = f ( x1 ,..., x j −1 , x j + x j , x j +1 ,..., xn ) − f ( x1 ,..., x j −1 , x j , x j +1 ,..., xn ) .

. 5 , " lim	x j u	, " "

x j → 0	x j

, * " 1- " & u = f ( x1 , x2 ,...xn )

x j , , * " "

∂u	=	∂f	= f ′ (x , x ,...x ) .
	=		= f ′ (x , x ,...x ) .
∂x j			x j	1 2	n
∂x j		∂x j

% "

∂f

( « ∂ » "

∂x j

, y = f ( x) ) ! .

. 5 !2.

2 " 2- u = f ( x, y) ,

∂u

∂x

∂u

, " 3- u = f ( x, y, z) –

∂u

∂y

∂x

∂y

∂z

2 * ,, "

! * " ,' , " 6 + ' * " . ) + + " ! *

( ', * " + , ( (

, .

. 2 ( .

z = arctg

& + ' y ', ,:

∂z

−

= −

+ y2

∂x

1 +

& + ' x ', ,:

∂z

∂y

1 +

x x2 + y2

2. z = 2x3 − 4x2 y + 5xy2 − 6 y3 .

∂z

= 6x2 − 8xy + 5 y2 ,

∂z

= −4x2 + 10xy −18 y 2 .

∂x

∂y

z = xe− xy .

∂z

= e− xy + xe− xy (− y ) = e− xy (1 − xy ),

∂x

∂z

= xe− xy (−x ) = −x2e− xy .

∂y

z = y x .

∂z

= y x ln y ;

∂z

= xy x −1 .

∂x

∂y

2 5 ! (1804–1851) – * (

" " , ' (*

" y = const ), y – ' ( x = const ).

5. u =

∂u

−

;

∂u

= −

;

∂u

= −

∂x y x2

∂y

∂z

6. )!

∂x

∂r

∂ϕ

∂θ

J =

∂y

∂r

∂ϕ

∂θ

∂z

∂r

∂ϕ

∂θ

x = r cosθ cosϕ ,

y = r cosθ sin ϕ , z = r sinθ (

+ ).

/ ,:

∂x

= cosθ cosϕ ,

∂x

= −r cosθ sin ϕ ,

∂x

= −r sinθ cosϕ ,

∂ϕ

∂r

∂θ

∂y

= cosθ sin ϕ ,

∂y

= r cosθ cosϕ ,

∂y

= −r sinθ sin ϕ ,

∂r

∂ϕ

∂θ

∂z

= sinθ ,

∂z

= 0 ,

∂z

= r cosθ .

∂ϕ

∂r

∂θ

) +:

cosθ cosϕ

−r cosθ sin ϕ

−r sinθ cosϕ

J =

cosθ sin ϕ

r cosθ cosϕ

−r sinθ sin ϕ

= r 2 cosθ

sinθ

r cosθ

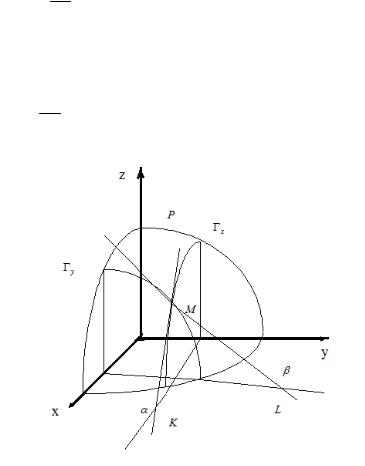
2’" , ( z = f ( x, y ).

. ( ! + " , , " " P ( . 9), M (x, y, z ) – ( .

% 6 y = const , , x , " " ", ! '

P ' ', * ' Oxz .

. ( MK – x M (x, y, z ), α – , (

,' ' " Ox . ) *

∂z	dz
	=	,
∂x
	dx y= const

( ,

, ,

∂z = tgα . ∂x

, " y – P ' x = const , β –

, ( ' Oy ' ML M (x, y, z ) y ,

∂z = tg β . ∂y

	$ . 7.
	8. .
. ( " u = f ( x1 , x2 ,..., xn )		"
M ( x , x ,..., x ) n . . x , x ,..., x
1 2	n	1 2	n
x1 , x2 ,...,	xn . & +, M ′( x1 +			x1 , x2 + x2 ,..., xn + xn ) D .
. 9 " u = f ( x1 , x2 ,..., xn )			, * " " !

M , " ( ( + ! ":

n	n
u = ∑Aj ( x1, x2 ,..., xn )	x j + ∑α j (x1, x2 ,..., xn , x1 , x2 ,..., xn ) x j ,	(9.1)
j =1	j =1

lim α j = 0 .
	x1 → 0
...
	xn → 0
	0 6 ( , "
				n
. 6 " * " ∑Aj x j , " (
				j =1
				n
			x1 , x2 ,..., xn . * " ∑α j x j		, "
				j =1
x1 → 0,...,			xn → 0 , ' ", +

	x2 +	x2	+ ... + x2 .
1		2	n
	. (, , , ' 2- u = f ( x, y) , "
M ( x, y) 2 . . x, y					x, y .

# " u = f ( x, y) , * " ( ' M , "

(		u = f ( x + x, y + y) − f ( x, y) + ! ":
u = A( x, y) x + B( x, y) y + α( x, y, x, y) x + β( x, y, x, y) y ,
A, B	x,	y + *, lim α = lim β = 0 .
			x→ 0	x→ 0
			y→ 0	y→ 0
. $" ' u = x2 y . : ( , ":
u = ( x + x)2 ( y + y) − x2 y = 2xy x + x2					y + y x2 + 2x x y + x2 y .
2xy	x + x2		y (	x,	y , y x2 + 2x x y +
+Δx2 y	x → 0,		y → 0 ", +

x2 + y2 . # " ( M ( x, y) .

. " u = f ( x1 , x2 ,..., xn ) " !

M ( x1 , x2 ,..., xn ) , ! .

. ) * " u = f ( x1 , x2 ,..., xn ) (

M , ( ( , ":

	n	n
u = ∑Aj		x j + ∑α j	x j ,
	j =1	j =1
,, lim			u = 0 , ( ,, " u = f ( x1 , x2 ,..., xn )
		x1 → 0
		...
		xn → 0
M .
. " u = f ( x1 , x2 ,..., xn ) " !
				∂u	( j =		).
M ( x , x ,..., x		) , M		∂u		1, n
M ( x , x ,..., x		) , M				1, n
1 2	n			∂x j
				∂x j
			20

. .( " u = f ( x1 , x2 ,..., xn ) ( M . # ( ( , ":

u = ∑Aj

x j + ∑α j

x j ,

j =1

α j → 0

x1 ,

x2 ,..., xn . % (

x2 = ... =

xn = 0 . # ( u

* " (

u , ,:

x u = A1 x1 + α1 x1 .

% ! ,

x1 (

x1 → 0 . :

lim

x u

= A1 .

x1 → 0

& ( , *

∂u

, +

∂x1

∂u

= A .

∂x1

∂u

= A ,...,

∂u

= A .

∂x2

∂xn

# " u = f ( x1 , x2 ,..., xn ) , M

∂u ,..., ∂u , ' *

∂x1

∂xn

, A1 ,..., An (9.1):

A =

∂u

, A =

∂u

,..., A =

∂u

(9.2)

∂x1

∂x2

∂xn

# .

2 " (9.2) * (9.1) ! , ":

∂u

u = ∑

x j + ∑α j x j .

(9.3)

∂x j

j =1

2 " 2- u = f ( x, y) ,:

u =

∂u

x +

∂u

y + αΔx + βΔy .

∂x

∂y

., " " u = x2 y ,:

A =

∂u

= 2xy, B =

∂u

= x2 .

∂x

∂y

! ". )! + " , , +, . 2,

<<< < Предыдущая 12 / 82 3 4 5 6 7 8 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.05.2025144.9 Кб0ДИПЛОМНА Марінов.doc
#
20.05.2015278.02 Кб17Дипломна работа Маша Станкова 4-болг332.doc
#
01.05.2025286.21 Кб0дипломна робота текст.doc
#
01.03.2025648.7 Кб0Дипломна робота.doc
#
01.04.20251.6 Mб0Диущак Юля.doc
#
20.05.2015813.81 Кб6Диференціальне числення ФБЗ.pdf
#
20.05.20151.08 Mб9Диференціальне числення ФОЗ.pdf
#
20.05.2015237.57 Кб11ДифференцПсихолЛекции.doc
#
20.05.2015983.01 Кб245Длекции с картинками.docx
#
12.11.2019259.07 Кб2Для 3 курсу _ПС.doc(3 перших заняття).doc
#
01.05.2025114.69 Кб0Для бакалавров.doc