§ 7. Однородная система линейных уравнений.
ФУНДАМЕНТАЛЬНАЯ
СИСТЕМА РЕШЕНИЙ.
Система
линейных алгебраических уравнений вида
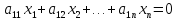



где
 и
и принадлежат
некоторому числовому полюk,
называется
однородной.
Набор ( 0, 0, … ,0 ), 0 €
k,
очевидно, является решением системы
(7.I), а поэтому однородная система всегда
совместна. Это же можно подтвердить и
теоремой Кронекера-Капелли, т.к.
принадлежат
некоторому числовому полюk,
называется
однородной.
Набор ( 0, 0, … ,0 ), 0 €
k,
очевидно, является решением системы
(7.I), а поэтому однородная система всегда
совместна. Это же можно подтвердить и
теоремой Кронекера-Капелли, т.к.
 ,
ибо присоединение к матрице нулевого
столбца не меняет ранга матрицы. Если
,
ибо присоединение к матрице нулевого
столбца не меняет ранга матрицы. Если ,
то система (7.I) имеет бесконечно много
решений, ибо в ступенчатом виде системы
(7.I) всегда будет
,
то система (7.I) имеет бесконечно много
решений, ибо в ступенчатом виде системы
(7.I) всегда будет . Если не
. Если не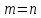 и
и ,
то система (7.I) имеет единственное решение
( 0, 0, … , 0 ) . Если не
,
то система (7.I) имеет единственное решение
( 0, 0, … , 0 ) . Если не и
и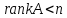 ,
то система (7.I) имеет бесконечно много
решений. Нас сейчас интересует тот
случай, когда
,
то система (7.I) имеет бесконечно много
решений. Нас сейчас интересует тот
случай, когда и
система (7.I) имеет бесконечно много
решений.
и
система (7.I) имеет бесконечно много
решений.


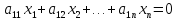



 и
и принадлежат
некоторому числовому полюk,
называется
однородной.
Набор ( 0, 0, … ,0 ), 0 €
k,
очевидно, является решением системы
(7.I), а поэтому однородная система всегда
совместна. Это же можно подтвердить и
теоремой Кронекера-Капелли, т.к.
принадлежат
некоторому числовому полюk,
называется
однородной.
Набор ( 0, 0, … ,0 ), 0 €
k,
очевидно, является решением системы
(7.I), а поэтому однородная система всегда
совместна. Это же можно подтвердить и
теоремой Кронекера-Капелли, т.к.
 ,
ибо присоединение к матрице нулевого
столбца не меняет ранга матрицы. Если
,
ибо присоединение к матрице нулевого
столбца не меняет ранга матрицы. Если ,
то система (7.I) имеет бесконечно много
решений, ибо в ступенчатом виде системы
(7.I) всегда будет
,
то система (7.I) имеет бесконечно много
решений, ибо в ступенчатом виде системы
(7.I) всегда будет . Если не
. Если не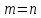 и
и ,
то система (7.I) имеет единственное решение
( 0, 0, … , 0 ) . Если не
,
то система (7.I) имеет единственное решение
( 0, 0, … , 0 ) . Если не и
и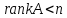 ,
то система (7.I) имеет бесконечно много
решений. Нас сейчас интересует тот
случай, когда
,
то система (7.I) имеет бесконечно много
решений. Нас сейчас интересует тот
случай, когда и
система (7.I) имеет бесконечно много
решений.
и
система (7.I) имеет бесконечно много
решений.