§5. Связь метода гаусса с теоремой кронекера-капелли

Применив метод Гаусса исключения неизвестных, можно сформулировать необходимое и достаточное условие совместности системы линейных уравнений, что мы и сделали в предыдущем параграфе. Но эта формулировка связана с конечным результатом: после приведения к ступенчатому виду не оказалось уравнений вида 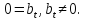Система же линейных уравнений определяется количеством неизвестных, коэффициентами при неизвестных и свободными членами, поэтому естественно искать необходимое и достаточное условие совместности систем линейных уравнений, связанное с заданными величинами: матрицей коэффициентов и расширенной матрицей системы. Как вы знаете, необходимым и достаточным условием, удовлетворяющим таким требованиям, является теорема Кронекера-Капелли. Напомним ее.

ТЕОРЕМА КРОНЕКЕРЕ-КАПЕЛЛИ: для того чтобы система линейных алгебраических уравнений была совместна, необходимо и достаточно, чтобы ранг расширенной матрицы системы равнялся рангу матрицы системы.

На языке обозначений это выглядит так:

Система (4.1) совместна 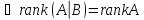, где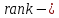ранг матрицы.

Но как вы знаете, ранг матрицы – это максимальное число линейно независимых строк матрицы или максимальное число независимых столбцов матрицы (эти числа совпадают), а найти максимальное число независимых строк матрицы можно , и проще всего с помощью элементарных преобразований строк, приводя матрицу к ступенчатому(трапецеидальному) виду. Реализуя на практике метод Гаусса с помощью расширенной матрицы 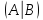системы линейных уравнений мы приводя систему к ступенчатому виду, одновременно находим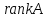и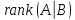и можем судить о совместности системы на основании теоремы Кронекера-Капелли. 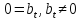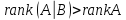Ситуацияи означает чтои система несовместна. 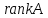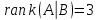В примере 4.1=2,а значит система несовместна. В примере 4.2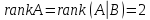– система совместна.

§6. Правело крамера и метод гаусса

Если число уравнений системы линейных алгебраических уравнений равно числу неизвестных и определитель матрицы коэффициентов системы отличен от нуля, то как следует из теоремы Кронекера-Капелли система совместна и имеет единственное решение. Крамер предложил это единственное решение находить с помощью определителей.

ПРАВИЛО КРАМЕРА. Если система линейных алгебраических уравнений:

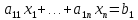
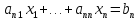
имеет отличный от нуля определитель матрицы коэффициентов системы

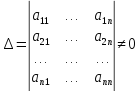
то ее единственное решение (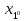,,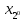 … ,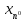) задается формулами

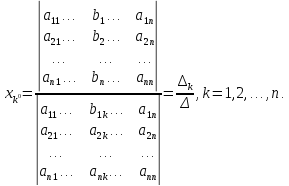
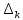получается заменой к –го столбца определителя ∆ столбцом свободных членов.

ПРИМЕР 6.I. Решить по правилу Крамера систему линейных уравнений

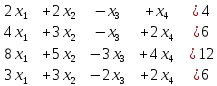
(6,1)

РЕШЕНИЕ. Найдем определитель матрицы коэффициентов системы (6,1)

Вычтем четвертый удвоенный столбец из первого, а затем разложим определитель по первому столбцу

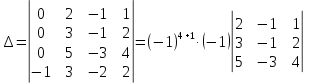
В определителе третьего порядка сделаем нули в первой строке. Для этого третий столбец прибавим ко второму и третий столбец умножив на – 2 прибавим к первому. Затем разложим определитель по элементам первой строки

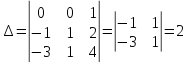
Т.е. ∆≠2 и система имеет единственное решение, которое можно найти по методу Крамера. Найдем :

В определителе из первого столбца вычтем удвоенный второй, из второго удвоенный четвертый, к третьему прибавим четвертый. Получим

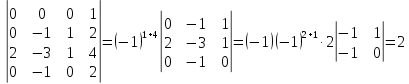
Откуда

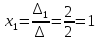
Найдем

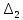
Четвертый столбец умножим на -2 и прибавим к первому, на -4 и прибавим ко второму, четвертый прибавим к третьему, получим

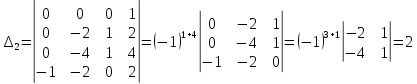
откуда

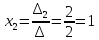
Найдем .

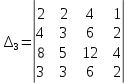
Делаем как и ранее нули в первой строке с помощью четвертого столбца

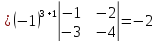
Откуда

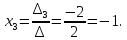
Осталось найти 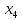. Мы имеем

Здесь мы второй столбец умножили на -2 и прибавили к четвертому. Разложив 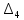по 4-ому столбцу, получаем

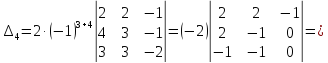
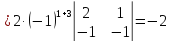
Таким образом

Единственным решением нашей системы является набор чисел (1, 1, -1, -1) .

Как мы убедились, решение системы по методу Крамера требует большой вычислительной работы. Решим эту же систему по методу Гаусса:

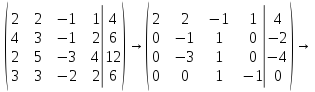
Мы первое уравнение умножили на 2 и вычли из второго, умножили на 4 и вычли из третьего, умножили четвертое уравнение на -2, первое на 3 и прибавили к четвертому. Затем второе уравнение умножили на -3 и прибавили к третьему:

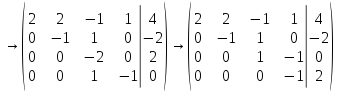(6,2)

Здесь мы поменяли местами третье и четвертое уравнение, а затем новое третье уравнение умножили на 2 и прибавили к четвертому. Система приведена к ступенчатому виду (6,2), имеет единственное решение ( 1, 1, -1, -1) .

Как видим метод Гаусса и в этом случае значительно проще. Методом Гаусса в практическом отношении пользоваться значительно выгоднее.

Но правило Крамера ( иногда в литературе называется теоремой Крамера ) имеет некоторую ценность при теоретических исследованиях и применяется при формулировке теорем в ряде других областей математики, поэтому знать его нужно.