
а11α1+а12 α 2+…+а1nαn=b1
а21α1+а21 α 2+…+а2nαn=b2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
аί1α1+аί2 α 2+…+аίnαn=bί (3.5)
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
аk1α1+аk2 α 2+…+аknαn=bk
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
am1α1+аm2 α 2+…+аmnαn=bm
Совершим
элементарное преобразование III
типа системой (3.I).т.
е. прибавим к ί-ому уравнению k-ое,
умноженное на число
 . Мы получаемсистему:
. Мы получаемсистему:
а11x1+a12x2+ . . .+a1nxn=b1
. . . . . . . . . . . . . . . . . . . . .
(aί1+cak1)x+. . .+(aίn+cakn)xn=bί+cbk
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (3.6)
ak1x1+ak2x2+ . . .+aknxn=bk
. . . . . . . . . . . . . . . . . . . . . .
am1x1+am2x2+ . . . +amnxn=bm
Подставляя набор чисел (α1, α2, . . .,αn) в систему (3.6) получаем:
a11α1 +. . . + a1nαn = b1
.. . . . . . . . . . . . . . . . . . . . . .
(aί1+cak1)α+ . . . +(aίn+cakn)αn = пока не знаем что
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (3.7)
ak1α1 + . . . + aknαn = bk
. . . . . . . . . . . . . . . . . . . . . . . .
am1α1 + . . . + amnαn = bm
ибо все остальные уравнения кроме ί –ого в системе (3.6) совпадают с уравнениями системы (3.І). Левую же часть ί-ого уравнения системы (3.6) после подстановки в нее набора (α1, . . . ,αn) можно записать как:
(aί1α1+ . . . +aίnαn)+cak1α1+ . . .+caknαn=(aί1α1+ . . .+aίnα1)+c(ak1α1+ . . .+aknαn)=bί+cbk
Значит (α1, α2, . . . ,αn) является решениеми ί –ого уравнения системы (3.6).
Таким образом мы показали, что всякое решение системы (3.І) является решением системы (3.6). Покажем , что имеет место и обратное: Пусть (β1, β2, . . . ,βn) – произвольное решение системы(3.6). Значит, имеет место набор верных числовых равенств:
а11β1+a12β2+ . . .+a1nβn=b1
. . . . . . . . . . . . . . . . . . . . .
(aί1+cak1)β1+. . .+(aίn+cakn)βn=bί+cbk
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (3.8)
ak1β1+ak2β2+ . . .+aknβn=bk
. . . . . . . . . . . . . . . . . . . . . .
am1β1+am2β2+ . . . +amnβn=bm
Так как (3.8) совокупность верных числовых равенств, то вычтем из ί-ого равенства k-ое, умноженное на с. Получим :
а11β1 +. . .+ a1nβn = b1
. . . . . . . . . . . . . . . .
aί1β1 +. . .+ aίnβn = bί
. . . . . . . . . . . . . . . . . . (3.9)
ak1β1 +. . .+ aknβn = bk
. . . . . . . . . . . . . . . . . . .
am1β1 +. . . + amnβn = bm
а это и означает, что всякое решение системы (3.6) является решением системы (3.І).
Итак, мы уже знаем те преобразования системы линейных уравнений, которые приводят ее к системе, эквивалентной исходной. Наша задача описать, как путем последовательного применения элементарных преобразований можно перейти от заданной системы к системе более простого вида. Эту задачу решил Гаусс и мы переходим к изложению метода Гаусса.
§4. Метод гаусса последовательного исключения неизвестных
Пусть нам дана произвольная система линейных уравнений:
a11x1+a12x2 + . . .+ a1nxn = b1
a21x1+a22x2 + . . . + a2nxn = b2
. . . . . . . . . . . . . . . . . . . . . . . . (4.I)
am1x1+am2x2+ . . . +amnxn = bm
где аij,
bk
(i=1,2,....,n;
j=1,2,...,m;
k=1,2,…,m)
принадлежат некоторому числовому полю .
.
Без ограничения
общности можем предложить, что а11 0,
ибо если а11
= 0, то применив элементарное преобразование
І
типа, поменяем местами первое уравнение
с таким j
–м что аj1
0,
ибо если а11
= 0, то применив элементарное преобразование
І
типа, поменяем местами первое уравнение
с таким j
–м что аj1 0.
Если все аk1
= 0 (k=1,2,
…,m)
то просто нет смысла говорить о переменной
х1
. Нам нужно из 2-го, 3-го и т. д. m-го
уравнения исключить переменную х1.
Повторим процесс исключения переменной
х1
в случае системы 2-х линейных уравнений
с двумя неизвестными, рассмотренный
ранее. Для этого умножим первое уравнение
на –
0.
Если все аk1
= 0 (k=1,2,
…,m)
то просто нет смысла говорить о переменной
х1
. Нам нужно из 2-го, 3-го и т. д. m-го
уравнения исключить переменную х1.
Повторим процесс исключения переменной
х1
в случае системы 2-х линейных уравнений
с двумя неизвестными, рассмотренный
ранее. Для этого умножим первое уравнение
на – и прибавим его ко второму, умножим
первое уравнение на –
и прибавим его ко второму, умножим
первое уравнение на – и прибавим к 3-му уравнению и т. Д. –
умножим первое уравнение на –
и прибавим к 3-му уравнению и т. Д. –
умножим первое уравнение на – и прибавим к последнему. Мы совершилиm-1
элементарное преобразование третьего
типа и пришли к системе, эквивалентной
исходной:
и прибавим к последнему. Мы совершилиm-1
элементарное преобразование третьего
типа и пришли к системе, эквивалентной
исходной:
a11x1+a12x2 + . . .+ a1nxn = b1
a’22x2 + . . . + a’2nxn = b’2
. . . . . . . . . . . . . . . . . . . (4.2)
a’m2x2+ . . . +a’mnxn = b’m
В (4.2) хk – неизвестное с наименьшим номером, которое входит в какое-нибудь уравнение, не считая первого. k может быть больше двух, т. к. может оказаться, что в процессе исключения х1исключилась и переменная х2,…,хк-1 . Оставив I уравнение без изменения, ко всем остальным применим те же рассуждения, что и ранее и исключаем из 3-го, 4-го,. . . ,m-го уравнений переменную хк . Будем применять этот процесс до тих пор, пока возможно. В конце концов система примет вид:

 +
. . . +
+
. . . +


. . . . . . . . . . . . . . . . . . . . . . . (4.3)
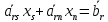

. . . . . . . . .

Здесь
 (что можно записать одним условием
(что можно записать одним условием
 , ибо в поле нет делителей нуля ( см. [2],
стр. 185, [I],
стр.279),
, ибо в поле нет делителей нуля ( см. [2],
стр. 185, [I],
стр.279),
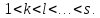 Может
оказатися, что
Может
оказатися, что
 и поэтому уравнений вида
и поэтому уравнений вида
 в системе (4.3) не будет. Систему вида
(4.3) называют системой ступенчатого (
или трапецеидального) вида.
в системе (4.3) не будет. Систему вида
(4.3) называют системой ступенчатого (
или трапецеидального) вида.
Так мы показали, что всякая система линейных уравнений (4.I) эквивалентна системе ступенчатого вида. Так как мы пришли к системе, эквивалентной исходной, то достаточно вопрос о совместности системы (4.I) и вопрос о числе решений системы (4.I) исследовать для систем ступенчатого вида.
1. СОВМЕСТНОСТЬ СИСТЕМЫ (4.3).
Если система
(4.3) содержит уравнение виде
 , где
, где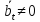 ,
то эта система несовместна, т.к. уравнение
,
то эта система несовместна, т.к. уравнение нельзя удовлетворить никаким значениям
для переменных
нельзя удовлетворить никаким значениям
для переменных .
Если таких уравнений в системе (4.3) нет,
то система совместна. В самом деле,
объявим
.
Если таких уравнений в системе (4.3) нет,
то система совместна. В самом деле,
объявим главными неизвестными ( мы это делаем
потому, что коэффициенты
главными неизвестными ( мы это делаем
потому, что коэффициенты отличны от нуля). Остальные переменные
назовем свободными. Придавая свободным
переменным произвольные значения и
подставляем их в систему (4.3) снизу вверх,
найдем наконец
отличны от нуля). Остальные переменные
назовем свободными. Придавая свободным
переменным произвольные значения и
подставляем их в систему (4.3) снизу вверх,
найдем наконец .
Таким образом значения для главных
неизвестных определяются однозначно
при любых значениях для свободных
неизвестных, ибо нам приходится каждый
разрешить уравнениеI
степени вида
.
Таким образом значения для главных
неизвестных определяются однозначно
при любых значениях для свободных
неизвестных, ибо нам приходится каждый
разрешить уравнениеI
степени вида
 .
.
Значит, для
совместной системы линейных уравнений
необходимо и достаточно, чтобы после
приведения ее к ступенчатому виду в ней
не оказалось уравнений вида
 .
.
2.
Если
в совместной системе есть свободные
переменные
(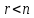 ),
то система неопределенная и имеет, как
нетрудно видеть, безконечно много
решений, ибо мы бесконечным числом
способов можем составлять из элементов
числового поля
),
то система неопределенная и имеет, как
нетрудно видеть, безконечно много
решений, ибо мы бесконечным числом
способов можем составлять из элементов
числового поля (содержащем бесконечно много элементов)
числовые наборы для свободных переменных.
(содержащем бесконечно много элементов)
числовые наборы для свободных переменных.
Если же у
совместной системе свободных неизвестных
нет и все неизвестные главные, то система
линейных уравнений является определенной.
Это имеет место тогда , когда в ступенчатом
виде
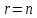 .
Болем подробно метод Гаусса см. [I],
стр. 15 – 23,( [2], стр. 23-33).
.
Болем подробно метод Гаусса см. [I],
стр. 15 – 23,( [2], стр. 23-33).
Отметим одно наблюдение. Каждой системе линейных уравнений ( 4.I) соответствует таблица коэффициентов этой системы вида:
 (4.4)
(4.4)
називаемая матрицей. Здесь . Вообще как вы знаете, матрицы изучаются и отдельно, независимо от систем линейных уравнений. Матрица вида (4.4) называется матрицей коэффициентов системы (4.I). В этой матрице есть строки:
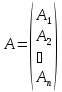 (4.5)
(4.5)
 - первая
строка матрицы
- первая
строка матрицы
 - вторая
строка матрицы
- вторая
строка матрицы
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
 - m-ая
строка матрицы
- m-ая
строка матрицы
и есть столбцы
 (4.6)
(4.6)


Если мы к матрице
А припишем
 -ым
столбе свободных членов
-ым
столбе свободных членов системы ( 4.I),
то получим так называемую расширенную
матрицу системы ( 4.I):
системы ( 4.I),
то получим так называемую расширенную
матрицу системы ( 4.I):
 (4.7)
(4.7)
Над строчками и столбцами матрицы А вводим элементарные преобразования типов I, II и III точно так же, как и в определенных 3.3, 3.4 и 3,5 с заменой слова «уравнение» словом «строка» («столбец»). Приводя систему (4.I) к ступенчатому виду (4.3) ми одновременно получаем такой факт:
Всякую матрицу с помощью элементарных преобразований можно привести к ступенчатому виду.
Рассмотрим ряд примеров на примере метода Гаусса.
ПРИМЕР 4.1. Выяснить, совместна ли система линейных уравнений и если да, то найти все ее решения.
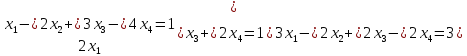 (4.8)
(4.8)
РЕШЕНИЕ. Как мы ранее отмечали, всякой системе линейных уравнений соответствует расширенная матрица вида ( 4.7). Так вот при практическом решении системы линейных уравнений методом Гаусса удобнее выписать расширенную матрицу системы, опустив неизвестные , и выполнить элементарные преобразования только строк расширенной матрицы. Мы имеем из (4.8)
 (4.9)
(4.9)
Первое уравнение
:строку матрицы (4.9) умножим на -2 и
прибавим ко второму, умножим на -3 и
прибавим к третьему. Такой процедурой
исключим
 и придем к расширенной матрице
и придем к расширенной матрице

 (4.10)
(4.10)
Затем второе
уравнение в (4.10) вычтем из третьего,
исключив
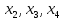 одновременно. Получим:
одновременно. Получим:
 (4.11)
(4.11)
Мы полностью реализовали метод Гаусса. Записав по расширенной матрице (4.11) систему имеем:

Получили равенство
 , что невозможно, поэтому система (4.8)
несовместна.
, что невозможно, поэтому система (4.8)
несовместна.
ПРИМЕР 4.2. Выяснить, совместна ли система линейных уравнений, и если да, то найти все ее решения:
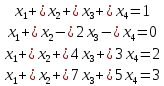 (4.12)
(4.12)
РЕШЕНИЕ. Мы имеем:


 (4.13)
(4.13)
Здесь мы сначала первое уравнение вычли из всех остальных, а затем второе прибавили к третьему , второе умножили на 2 и прибавили к четвертому уравнению.
В (4.13) не получили
противоречного уравнения вида
 ,а
потому система совместна. Из (4.13) имеем:
,а
потому система совместна. Из (4.13) имеем:
 (4.14)
(4.14)
Главными неизвестными
являются
 и
и ,
свободными-
,
свободными- и
и .
Теперь по ступенькам ступенчатого вида
(4.14) снизу вверх. Из второго уравнения
получаем:
.
Теперь по ступенькам ступенчатого вида
(4.14) снизу вверх. Из второго уравнения
получаем:
 (4.15)
(4.15)
Из первого уравнения
(4.14), подставив вместо правую часть (4.15), находим:
правую часть (4.15), находим:

Таким образом мы
можем написать систему линейных
уравнений:
 (4.16)
(4.16)
элементарную исходной, в которой выделены свободные неизвестные и главные независимые, которые можно найти через свободные.
Совокупность решений вида(4.16) называется общим решением системы.
Придавая свободным
неизвестным произвольные действительные
значения, мы получим все бесконечное
множество решений неопределенной
системы (4.12). ( у нас
 а
потом совместная система (4.12) имеет
бесконечно много решений). Положив,
например,
а
потом совместная система (4.12) имеет
бесконечно много решений). Положив,
например, получаем частное решение:
получаем частное решение:

ЗАМЕЧАНИЕ.
Вы, наверное,
уже заметили, как удобно, если
 и коэффициенты, получающиеся при главных
неизвестных, тоже малы или равны 0. Этого
всегда можно добиться. Прежде чем решать
систему по методу Гаусса, нужно внимательно
посмотреть на элементы
и коэффициенты, получающиеся при главных
неизвестных, тоже малы или равны 0. Этого
всегда можно добиться. Прежде чем решать
систему по методу Гаусса, нужно внимательно
посмотреть на элементы . Если среди них есть 1, например,
. Если среди них есть 1, например, то совершив элементарное преобразованиеI
типа, то есть переставить 1-ое и k-ое
уравнения, выведем на место “11” число
1.
то совершив элементарное преобразованиеI
типа, то есть переставить 1-ое и k-ое
уравнения, выведем на место “11” число
1.
ПРИМЕР 4.3. Пользуясь методом Гаусса, решить систему:
 (4.17)
(4.17)
РЕШЕНИЕ. Составляем расширенную матрицу:


Переставим первое и третье уравнения местами:


Вычтем из третьего уравнения второе, умножим второе на -4 и прибавим к четвертому:

Умножим четвертое уравнение на 2 и прибавим ко второму:

Умножим третье уравнение на -19 и прибавим к четвертому
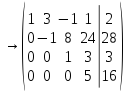
Система совместна
и имеет единственное решение, т.к.
 Запишем систему, эквивалентную системе
(4.17):
Запишем систему, эквивалентную системе
(4.17):
 (4.18)
(4.18)
Поднимаясь по ступенькам снизу вверх, в (4.18), получаем:

Решением системы является набор действительных чисел:

ЗАМЕЧАНИЕ.
Если среди элементов
 нет единицы, ее можно “сделать”, применяя
элементарное преобразования к уравнениям
системы.
нет единицы, ее можно “сделать”, применяя
элементарное преобразования к уравнениям
системы.
ПРИМЕР4.4. Применяя метод Гаусса, исследовать совместна ли система, и если да, найти все ее решения.
 (4.19)
(4.19)
РЕШЕНИЕ. Поменяем местами первое и второе уравнение:

Здесь мы из третьего уравнения вычли первое. Вычтем из первого уравнения второе:

Здесь мы сначала ко второму уравнению прибавили первое, умноженное на -2, разделим третье, умноженное на 4. Теперь умножая второе на 2 и прибавляя к третьему, окончательно получим:

или

Система линейных
уравнений совместна и имеет бесконечно
много решений, ибо

Общее решение системы (4.19):


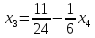
Частное решение системы (4.19):

