
- •Линейная алгебра глава 1 законы композиции
- •§1. Внутренние законы композиции
- •1.2. Основные алгебраические образования: группы, кольца, поля
- •§2. Внешние законы композиции
- •§3. Изоморфизм
- •Глава 2 комплексные числа
- •§1. Поле с комплексных чисел
- •Потренироваться в сложении-вычитании и умножении
- •§2. Комплексно сопряженные числа
- •§3. Модуль комплексного числа. Деление двух комплексных чисел
- •§4. Геометрическая интерпретация комплексных чисел
- •§5. Тригонометрическая форма комплексного числа. Формула муавра. Извлечение корня
- •§6. Комплексные функции
- •Комплексные функции одного действительного переменного
- •Показательная функция zеz с комплексным показателем и ее свойства
- •Формулы Эйлера. Показательная форма комплексного числа
- •Глава 3 многочлены
- •§1. Кольцо многочленов
- •§2. Деление многочленов по убывающим степеням
- •§3. Взаимно простые и неприводимые многочлены. Теорема и алгоритм евклида
- •§4. Нули (корни) многочлена. Кратность нуля. Разложение многочлена в произведение неприводимых многочленов над полем с и r
- •Упражнения
- •Глава 4 векторные пространства
- •§1. Векторное пространство многочленов над полем p коэффициентов
- •§2. Векторные пространства р n над полем р
- •§3. Векторы в геометрическом пространстве
- •3.1. Типы векторов в геометрическом пространстве
- •Из подобия треугольников авс и ав'с' следует (как в случае , так и в случае ), что.
- •3.3. Задание свободных векторов при помощи декартовой системы координат и соответствие их с векторами из векторного пространства r3
- •3.4. Скалярное произведение двух свободных векторов
- •Упражнения
- •§4. Векторное подпространство
- •4.1. Подпространство, порожденное линейной комбинацией векторов
- •4.2. Линейная зависимость и независимость векторов
- •4.3. Теоремы о линейно зависимых и линейно независимых векторах
- •4.4. База и ранг системы векторов. Базис и размерность векторного подпространства, порожденного системой векторов
- •4.5. Базис и размерность подпространства, порожденного системой
- •§5. Базис и размерность векторного пространства
- •5.1. Построение базиса
- •5.2. Основные свойства базиса
- •5.3. Базис и размерность пространства свободных векторов
- •§6. Изоморфизм между n – мерными векторными пространствами к и р n над полем р
- •§8. Линейные отображения векторных пространств
- •8.1. Ранг линейного отображения
- •8.2. Координатная запись линейных отображений
- •Упражнения
- •Глава 5 матрицы
- •§1. Ранг матрицы. Элементарные преобразования матриц
- •§2. Алгебраичесие операции над матрицами.
- •Пусть даны матрицы
- •§3. Изоморфизм между векторным пространством
- •§4. Скалярное произведение двух векторов из пространства Rn
- •§5. Квадратные матрицы
- •5.1. Обратная матрица
- •5.2. Транспонированная квадратная матрица.
- •Упражнения
- •Глава 6 определители
- •§1. Определение и свойства определителя, вытекающие из определения
- •§2. Разложение определителя по элементам столбца (строки). Теорема о чужих дополнениях
- •§3. Геометрическое представление определителя
- •3.1. Векторное произведение двух свободных векторов
- •3.2. Смешанное произведение трех свободных векторов
- •§4. Применение определителей для нахождения ранга матриц
- •§5. Построение обратной матрицы
- •Упражнения
- •Глава 7 системы линейных уравнений
- •§1. Определения. Совместные и несовместные системы
- •§2. Метод гаусса
- •§3. Матричная и векторная формы записи линейных
- •3. Матрицу-столбец свободных членов размер матрицыk 1.
- •§4. Система крамера
- •§5. Однородная система линейных уравнений
- •§6. Неоднородная система линейных уравнений
- •Упражнения
- •Глава 8 приведение матриц
- •§1. Матрица перехода от одного базиса к другому
- •1.1. Матрица перехода, связанная с преобразованием
- •1.2. Ортогональные матрицы перехода
- •§2. Изменение матрицы линейного отображения при замене базисов
- •2.1. Собственные значения, собственные векторы
- •2.2. Приведение квадратной матрицы к диагональной форме
- •§3. Вещественные линейные и квадратичные формы
- •3.1. Приведение квадратичной формы к каноническому виду
- •3.2. Определенная квадратичная форма. Критерий Сильвестра
- •Упражнения (номера с 1465 и далее)
§3. Вещественные линейные и квадратичные формы
Рассмотрим
векторное пространство Rn
над полем
R,
в котором
задан базис
![]() и пусть
и пусть![]() –
произвольный
вектор этого пространства, iR.
–
произвольный
вектор этого пространства, iR.
Определение
1.
Вещественной
линейной
формой
называется линейное отображение
пространства Rn
в R,
которое каждому
![]() ставит в соответствие число
ставит в соответствие число![]() изR, где
i
и i
– числа из R.
Линейную форму называют также однородной
формой первой степени, и чаще всего ее
записывают в следующем виде:
изR, где
i
и i
– числа из R.
Линейную форму называют также однородной
формой первой степени, и чаще всего ее
записывают в следующем виде:
![]() ,
где
,
где![]() .
.
![]() Определение
2.
Вещественной квадратичной
формой
называется линейное отображение Rn
в R,
которое
каждому
Определение
2.
Вещественной квадратичной
формой
называется линейное отображение Rn
в R,
которое
каждому
![]() ставит в соответствие число
ставит в соответствие число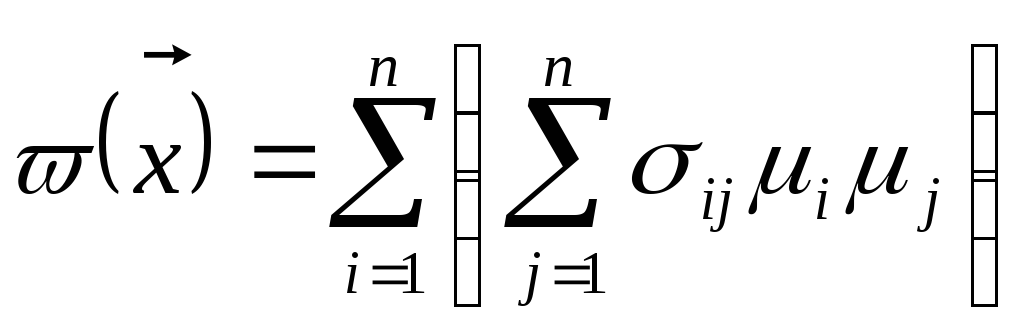 изR, где
изR, где
![]() – координаты
вектора
– координаты
вектора
![]() ,
,![]() – числа изR,
для которых
выполняется равенство
– числа изR,
для которых
выполняется равенство
![]() .
.
Из
определения следует, что
![]() .
Поэтому квадратичная форма есть
однородная форма второй степени.
.
Поэтому квадратичная форма есть
однородная форма второй степени.
Пример.
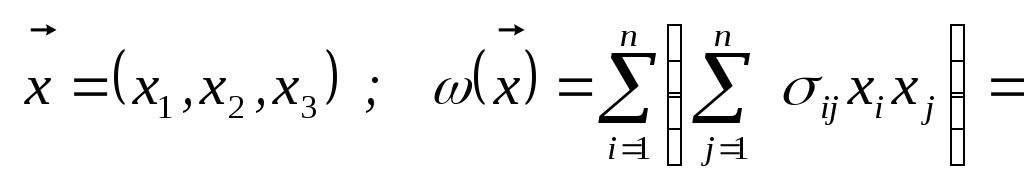
=![]()
![]()
![]()
3.1. Приведение квадратичной формы к каноническому виду
Квадратичную
форму можно записать и при помощи
матрицы. Для этого вектору
![]() изRn
поставим в
соответствие две матрицы: матрицу-столбец
изRn
поставим в
соответствие две матрицы: матрицу-столбец
 и матрицу-строкуX
Т
= (
n).
Ясно, что X Т
является транспонированной матрицей
к X.
Для коэффициентов ij
квадратичной
формы введем действительную матрицу
и матрицу-строкуX
Т
= (
n).
Ясно, что X Т
является транспонированной матрицей
к X.
Для коэффициентов ij
квадратичной
формы введем действительную матрицу
 .
Тогда
.
Тогда
 .
.
Матрица А называется матрицей квадратичной формы и поскольку для коэффициентов квадратичной формы ij ji, то матрица А является симметрической.
Рассмотрим,
как изменяется матрица А
при переходе в Rn
от одного ортонормированного базиса к
другому. Обозначим матрицу перехода
через Т,
а координаты вектора
![]() в новом базисе через
в новом базисе через![]() .
Тогда
.
Тогда![]() ,
или в матричной формеX
= TY, где Т
ортогональная матрица. Поэтому для
квадратичной формы имеем
,
или в матричной формеX
= TY, где Т
ортогональная матрица. Поэтому для
квадратичной формы имеем
![]() ,
гдеВ = ТТАТ.
,
гдеВ = ТТАТ.
Но так как Т ортогональна, то ТТ = Т–1 ; значит В = Т–1АТ, т.е. В преобразована из А посредством матрицы Т. Кроме того, преобразованная матрица В – тоже симметрическая, ибо
ВТ = (Т–1АТ)Т = (ТТАТ)Т = ТТАТ(ТТ)Т = ТТАТ = В.
Поскольку АТ = А.
Так
как матрица А
симметрическая, то Rn
обладает хотя бы одним ортонормированным
базисом
![]() ,
составленным из собственных векторов
матрицыА;
тогда если в качестве нового базиса
выбрать базис
,
составленным из собственных векторов
матрицыА;
тогда если в качестве нового базиса
выбрать базис
![]() ,
то преобразованная матрица в этом базисе
,
то преобразованная матрица в этом базисе![]() и имеет диагональный вид
и имеет диагональный вид

здесь собственные значения i матрицы А могут быть как различные, так и совпадающие, но все действительные. Если матрица квадратичной формы диагональная, то квадратичная форма принимает вид:
![]() ,
гдеz1,
z2,
... zn
–
координаты вектора
,
гдеz1,
z2,
... zn
–
координаты вектора
![]() ,
разложенным по базису
,
разложенным по базису![]() .
.
Таким
образом, относительно базиса
![]() ,
составленного из собственных векторов
матрицы квадратичной формы, квадратичная
форма имеет только члены с квадратами;
говорят, что она приведена кканоническому
виду.
,
составленного из собственных векторов
матрицы квадратичной формы, квадратичная
форма имеет только члены с квадратами;
говорят, что она приведена кканоническому
виду.
Пример. Привести к каноническому виду квадратичную форму
![]() =
3х
=
3х![]() + 4х1х2
+ х
+ 4х1х2
+ х![]() ,
где
,
где![]() .
.
Составляем матрицу квадратичной формы:
 (см.
пример в начале параграфа).
(см.
пример в начале параграфа).
Записываем характеристическое уравнение
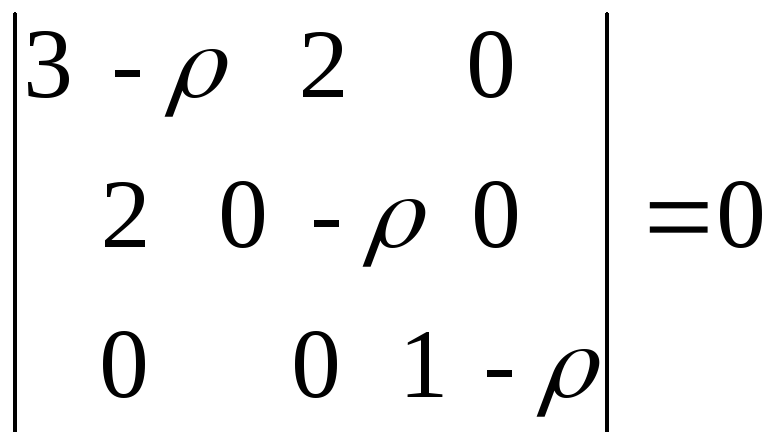 ,
откуда
.
,
откуда
.![]()
Решая последнее уравнение, находим собственные числа:
3
.
Обозначим координаты вектора
![]() в системе собственных векторов матрицы
черезz1,
z2,
z3.
Тогда квадратичная форма имеет вид
в системе собственных векторов матрицы
черезz1,
z2,
z3.
Тогда квадратичная форма имеет вид
![]() .
.
Находим ортонормированные собственные вектора матрицы:
![]() ;
;
![]() ;
;![]() .
Для этого уравнениеА(
.
Для этого уравнениеА(![]() )
=
)
=![]() записываем
в координатной форме:
записываем
в координатной форме:
 или
или
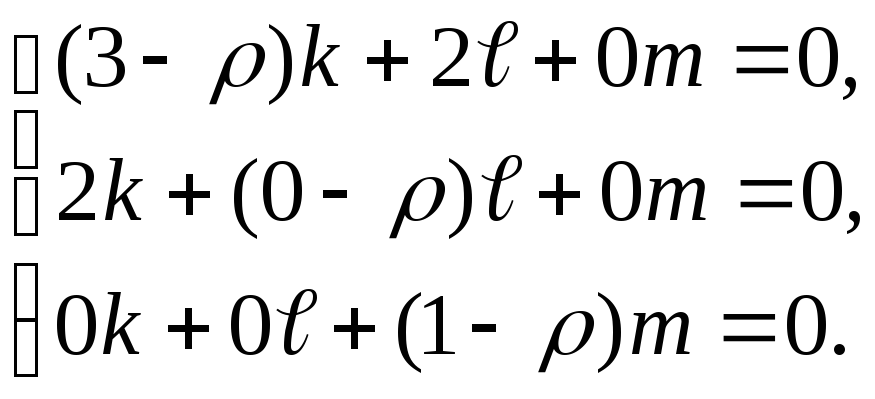
Положим
![]()
![]() .
Тогда система принимает вид:
.
Тогда система принимает вид:

Эта
сиcтема
имеет единственное решение
![]() ,
,![]() .
Величина компоненты
.
Величина компоненты
![]() любая. Чтобы вектор
любая. Чтобы вектор
![]() был нормированным, т.е. чтобы
был нормированным, т.е. чтобы![]() ,
примем
,
примем![]() .
Имеем
.
Имеем![]() .
.
Поскольку
![]() ,
то система принимает вид:
,
то система принимает вид:

Отсюда
![]() ,
,![]() ,
,![]() ,
где
,
где![]() любое действительное число. Нормируя,
получаем
любое действительное число. Нормируя,
получаем![]()
![]() ;
;![]() ;
;![]() .
Следовательно,
.
Следовательно,![]() .
.
Для
третьего собственного числа
![]() имеем систему:
имеем систему:
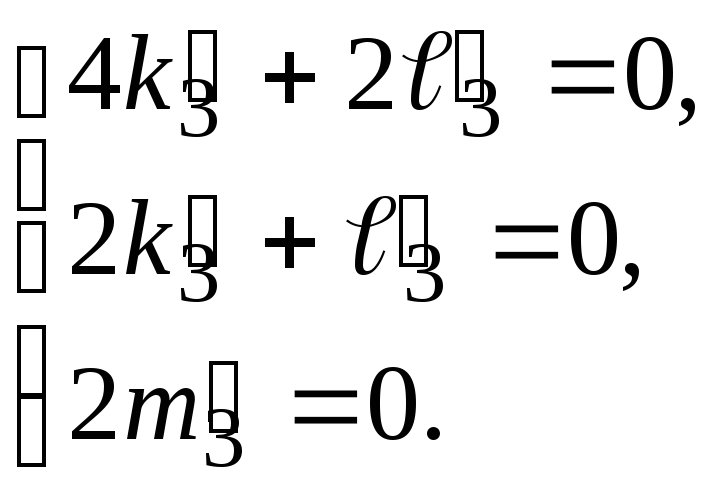
Отсюда
![]() ,
,![]() ,
,![]() ,
где
,
где![]() –
любое действительное число. Нормируя
–
любое действительное число. Нормируя![]() ,
находим
,
находим![]() ,
,![]() ,
,![]() ,
т.е. вектор
,
т.е. вектор![]() .
Таким образом, собственные векторы
квадратичной формы:
.
Таким образом, собственные векторы
квадратичной формы:![]() ,
,![]() ,
,![]() ,
а каноническая форма квадратичной
формы:
,
а каноническая форма квадратичной
формы:![]() .
.
