
- •Линейная алгебра глава 1 законы композиции
- •§1. Внутренние законы композиции
- •1.2. Основные алгебраические образования: группы, кольца, поля
- •§2. Внешние законы композиции
- •§3. Изоморфизм
- •Глава 2 комплексные числа
- •§1. Поле с комплексных чисел
- •Потренироваться в сложении-вычитании и умножении
- •§2. Комплексно сопряженные числа
- •§3. Модуль комплексного числа. Деление двух комплексных чисел
- •§4. Геометрическая интерпретация комплексных чисел
- •§5. Тригонометрическая форма комплексного числа. Формула муавра. Извлечение корня
- •§6. Комплексные функции
- •Комплексные функции одного действительного переменного
- •Показательная функция zеz с комплексным показателем и ее свойства
- •Формулы Эйлера. Показательная форма комплексного числа
- •Глава 3 многочлены
- •§1. Кольцо многочленов
- •§2. Деление многочленов по убывающим степеням
- •§3. Взаимно простые и неприводимые многочлены. Теорема и алгоритм евклида
- •§4. Нули (корни) многочлена. Кратность нуля. Разложение многочлена в произведение неприводимых многочленов над полем с и r
- •Упражнения
- •Глава 4 векторные пространства
- •§1. Векторное пространство многочленов над полем p коэффициентов
- •§2. Векторные пространства р n над полем р
- •§3. Векторы в геометрическом пространстве
- •3.1. Типы векторов в геометрическом пространстве
- •Из подобия треугольников авс и ав'с' следует (как в случае , так и в случае ), что.
- •3.3. Задание свободных векторов при помощи декартовой системы координат и соответствие их с векторами из векторного пространства r3
- •3.4. Скалярное произведение двух свободных векторов
- •Упражнения
- •§4. Векторное подпространство
- •4.1. Подпространство, порожденное линейной комбинацией векторов
- •4.2. Линейная зависимость и независимость векторов
- •4.3. Теоремы о линейно зависимых и линейно независимых векторах
- •4.4. База и ранг системы векторов. Базис и размерность векторного подпространства, порожденного системой векторов
- •4.5. Базис и размерность подпространства, порожденного системой
- •§5. Базис и размерность векторного пространства
- •5.1. Построение базиса
- •5.2. Основные свойства базиса
- •5.3. Базис и размерность пространства свободных векторов
- •§6. Изоморфизм между n – мерными векторными пространствами к и р n над полем р
- •§8. Линейные отображения векторных пространств
- •8.1. Ранг линейного отображения
- •8.2. Координатная запись линейных отображений
- •Упражнения
- •Глава 5 матрицы
- •§1. Ранг матрицы. Элементарные преобразования матриц
- •§2. Алгебраичесие операции над матрицами.
- •Пусть даны матрицы
- •§3. Изоморфизм между векторным пространством
- •§4. Скалярное произведение двух векторов из пространства Rn
- •§5. Квадратные матрицы
- •5.1. Обратная матрица
- •5.2. Транспонированная квадратная матрица.
- •Упражнения
- •Глава 6 определители
- •§1. Определение и свойства определителя, вытекающие из определения
- •§2. Разложение определителя по элементам столбца (строки). Теорема о чужих дополнениях
- •§3. Геометрическое представление определителя
- •3.1. Векторное произведение двух свободных векторов
- •3.2. Смешанное произведение трех свободных векторов
- •§4. Применение определителей для нахождения ранга матриц
- •§5. Построение обратной матрицы
- •Упражнения
- •Глава 7 системы линейных уравнений
- •§1. Определения. Совместные и несовместные системы
- •§2. Метод гаусса
- •§3. Матричная и векторная формы записи линейных
- •3. Матрицу-столбец свободных членов размер матрицыk 1.
- •§4. Система крамера
- •§5. Однородная система линейных уравнений
- •§6. Неоднородная система линейных уравнений
- •Упражнения
- •Глава 8 приведение матриц
- •§1. Матрица перехода от одного базиса к другому
- •1.1. Матрица перехода, связанная с преобразованием
- •1.2. Ортогональные матрицы перехода
- •§2. Изменение матрицы линейного отображения при замене базисов
- •2.1. Собственные значения, собственные векторы
- •2.2. Приведение квадратной матрицы к диагональной форме
- •§3. Вещественные линейные и квадратичные формы
- •3.1. Приведение квадратичной формы к каноническому виду
- •3.2. Определенная квадратичная форма. Критерий Сильвестра
- •Упражнения (номера с 1465 и далее)
§5. Однородная система линейных уравнений
Система линейных уравнений называется однородной, если правые части этих уравнений равны нулю:
 a1x1
+
a12
x2
+
... + a1n
xn
=
0,
a1x1
+
a12
x2
+
... + a1n
xn
=
0,
a21x1 + a22 x2 + ... + a2n xn = 0,
...................................... (7.8)
ak1x1 + ak2 x2 + .... + akn xn = 0.
Однородная
система всегда совместна, так как
расширенная матрица отличается от
основной на столбец, представляющий
нуль-вектор. Поскольку система, содержащая
нуль-вектор, всегда линейно зависима,
то ранг расширенной матрицы совпадает
с рангом основной матрицы. Совместность
однородной системы очевидна, так как
она всегда имеет тривиальное решение
х1 = х2 =.....= хп = 0.
Это решение
будет единственным, если однородная
система есть система Крамера, т.е. когда
k = n и
определитель D(A)
основной матрицы A
отличен от нуля. Другими словами, когда
ранг r(A)
основной матрицы равен числу n
неизвестных системы: r(A)
= n. Если же
r(A)
<
n, то однородная
система линейных уравнений имеет
бесчисленное множество решений и
совокупность решений системы образует
векторное подпространство. Покажем
это. Для этого запишем систему (7.8) в
векторной форме в пространстве Rn
вектор-строк.
В этом случае каждое уравнение системы
представляет собой скалярное произведение
двух векторов из Rn:
![]() и
и
![]() :
:

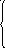
![]() (7.9)
(7.9)
Докажем,
что если вектора
![]() и
и![]() есть решения системы (7.9), то
есть решения системы (7.9), то![]() и
и![]() также
будут решениями этой системы. Действительно,
так как скалярное произведение
дистрибутивно относительно сложения
векторов и ассоциативно относительно
умножения на число, имеем:
также
будут решениями этой системы. Действительно,
так как скалярное произведение
дистрибутивно относительно сложения
векторов и ассоциативно относительно
умножения на число, имеем:

Отсюда
следует, что
![]() и
и![]() являются
также решениями однородной системы.
Кроме этого, нейтральный (0,0,....,0) и
симметричный
являются
также решениями однородной системы.
Кроме этого, нейтральный (0,0,....,0) и
симметричный![]() элементы также принадлежат пространству
решений. Таким образом, совокупность
решений однородной системы образует
векторное подпространство. Теперь
определим размерность подпространства
решений системы и построим его базис.
Как мы уже сказали, подпространство
решений содержит ненулевые вектора,
еслиr(A)
< n.
Условие r(A)
< n
всегда выполнено, если число k
уравнений системы меньше числа n
неизвестных. Тот факт, что ранг основной
матрицы A
равен r(A),
означает, что матрица A
содержит минор порядка r,
отличный от нуля; все же миноры более
высоких порядков равны нулю, в том числе
(если он существует) и минор порядка n.
Не ограничивая общности, можно считать,
что этим минором является главный минор
матрицы A
порядка r.
элементы также принадлежат пространству
решений. Таким образом, совокупность
решений однородной системы образует
векторное подпространство. Теперь
определим размерность подпространства
решений системы и построим его базис.
Как мы уже сказали, подпространство
решений содержит ненулевые вектора,
еслиr(A)
< n.
Условие r(A)
< n
всегда выполнено, если число k
уравнений системы меньше числа n
неизвестных. Тот факт, что ранг основной
матрицы A
равен r(A),
означает, что матрица A
содержит минор порядка r,
отличный от нуля; все же миноры более
высоких порядков равны нулю, в том числе
(если он существует) и минор порядка n.
Не ограничивая общности, можно считать,
что этим минором является главный минор
матрицы A
порядка r.
 .
.
Это всегда можно добиться, переставляя местами уравнения в системе. Тогда остальные к – r уравнений системы являются линейными комбинациями первых r уравнений системы и поэтому, не нарушая равносильности системы, эти уравнения из системы можно исключить. Оставшиеся же r уравнений системы запишем в следующем виде
 (7.10)
(7.10)
Заметим,
что если неизвестным xr+1,
. . .,
хn
в системе (7.10) придать какие либо числовые
значения, то получим систему Крамера,
так как
![]() и, следовательно, остальные неизвестныех1,
х2,
. . ., хr
можно определить однозначно по правилу
Крамера (7.7). Определим неизвестные х1,
х2,
. . ., хr
придавая для неизвестных хr+1,
хr+2,
. . ., хn
последовательно следующие значения
(1,0,...,0), (0,1,0,...,0),. . . , (0,0,. . . , 1). Такой выбор
обусловлен тем, что каждый набор из
n – r
чисел есть вектор канонического базиса
пространства Rn-r.
Положим, что для каждого указанного
набора значений хr+1,
хr+2,
. . ., хn
для х1,
х2,
. . ., хr
получены соответственно следующие n
– r
наборов из r
чисел
и, следовательно, остальные неизвестныех1,
х2,
. . ., хr
можно определить однозначно по правилу
Крамера (7.7). Определим неизвестные х1,
х2,
. . ., хr
придавая для неизвестных хr+1,
хr+2,
. . ., хn
последовательно следующие значения
(1,0,...,0), (0,1,0,...,0),. . . , (0,0,. . . , 1). Такой выбор
обусловлен тем, что каждый набор из
n – r
чисел есть вектор канонического базиса
пространства Rn-r.
Положим, что для каждого указанного
набора значений хr+1,
хr+2,
. . ., хn
для х1,
х2,
. . ., хr
получены соответственно следующие n
– r
наборов из r
чисел
![]()
![]() .
. .
.
. .![]() Ясно, что векторы
Ясно, что векторы
 (7.11)
(7.11)
являются
решениями системы (7.10). Число координат
у
векторов
![]() равноn
и они принадлежат пространству Rn.
равноn
и они принадлежат пространству Rn.
Докажем,
что векторы
![]() линейно независимы. Действительно, если
равенство
линейно независимы. Действительно, если
равенство![]() записать в скалярной форме
записать в скалярной форме
![]() ,
,
используя
компоненты (7.11), то оно выполняется
лишь при условии
n-r
= 0.
Это
непосредственно вытекает из уравнений,
для которых j r + 1.
Нетрудно показать также то, что любое
решение
![]() однородной системы (7.10) является линейной
комбинацией векторов
однородной системы (7.10) является линейной
комбинацией векторов![]() с коэффициентами
с коэффициентами![]() т.е.
т.е.
![]() ,
(7.12)
,
(7.12)
где
![]() могут принимать любые значения изR.
Для доказательства этого при решении
системы (7.10) для неизвестных xr+1,...,xn
полагаем значения (r+1,
0,..., 0), (0,
r+2,
0,…,0),.....,(0,0,...,n).
могут принимать любые значения изR.
Для доказательства этого при решении
системы (7.10) для неизвестных xr+1,...,xn
полагаем значения (r+1,
0,..., 0), (0,
r+2,
0,…,0),.....,(0,0,...,n).
Таким
образом, векторы
![]() с компонентами (7.11) образуют базис
подпространства решений однородной
системы (7.8) размерностиn
– r.
Выражение (7.12), определяющее все множество
решений подпространства, называется
общими
решениями однородной системы. Совокупность
линейно независимых решений
с компонентами (7.11) образуют базис
подпространства решений однородной
системы (7.8) размерностиn
– r.
Выражение (7.12), определяющее все множество
решений подпространства, называется
общими
решениями однородной системы. Совокупность
линейно независимых решений
![]() системы называетсяфундаментальной
системой
решений. Переменные xr+1,...,xn
называются свободными,
x1,...,xr
– базисными.
системы называетсяфундаментальной
системой
решений. Переменные xr+1,...,xn
называются свободными,
x1,...,xr
– базисными.
Замечание. Построение фундаментальных решений, проведенное нами выше, не является обязательным и при решении конкретных задач выбор значений xr+1,...,xn может быть другим.
Пример. Пусть дана однородная система уравнений
 x1
+ 2x2
– 5x3
+ 3x4
= 0,
x1
+ 2x2
– 5x3
+ 3x4
= 0,
2x1 + 5x2 – 6x3 – x4 = 0,
5x1 + 12x2 – 17x3 + x4 = 0,
в которой число неизвестных n = 4, а число уравнений к = 3. Поскольку к n то r(A) n и, следовательно, система имеет бесчисленное множество решений. Для построения фундаментальных и общего решений системы определим ранг r(A) основной матрицы

Рассмотрим
главные миноры:

 Для матрицыА
существует еще один минор третьего
порядка
Для матрицыА
существует еще один минор третьего
порядка
 но он также равен нулю. Таким образом,
все миноры третьего порядка матрицыА,
равны нулю, а среди миноров второго
порядка есть минор отличный от нуля.
Следовательно, ранг r(A)
матрицы А
равен 2. Это означает также, что третье
уравнение системы есть линейная
комбинация первых двух и его из системы
можно исключить. Действительно, третье
уравнение получается, если второе
уравнение умножить на 2 и сложить с
первым. После исключения из системы
третьего уравнения, оставшиеся два
уравнения, перепишем в следующем виде
но он также равен нулю. Таким образом,
все миноры третьего порядка матрицыА,
равны нулю, а среди миноров второго
порядка есть минор отличный от нуля.
Следовательно, ранг r(A)
матрицы А
равен 2. Это означает также, что третье
уравнение системы есть линейная
комбинация первых двух и его из системы
можно исключить. Действительно, третье
уравнение получается, если второе
уравнение умножить на 2 и сложить с
первым. После исключения из системы
третьего уравнения, оставшиеся два
уравнения, перепишем в следующем виде
 х1
+ 2х2
= 5х3
– 3х4,
х1
+ 2х2
= 5х3
– 3х4,
2х1 + 5х2 = 6х3 + х4.
Полагая
х3
= 1, а х4
= 0, получим фундаментальное решение
![]() системы
системы
 х1
+ 2х2
= 5,
х1
+ 2х2
= 5,
2х1
+ 5х2
= 6
х1
= 13, х2
= – 4,
![]() = (13, – 4, 1, 0).
= (13, – 4, 1, 0).
Полагая
х3
= 0, а х4
= 1, определим
![]()
 х1
+ 2х2
= –3,
х1
+ 2х2
= –3,
2х1
+ 5х2
= 1
х1
= –17, х2
= 7,
![]() =
(–17, 7, 0, 1).
=
(–17, 7, 0, 1).
Общее решение системы
![]()
![]()
где
![]() любые числа изR.
любые числа изR.
Итак, решения системы составляют векторное подпространство размерности n – r = 4 – 2 = 2.
