§3. Изоморфизм между векторным пространством

МАТРИЦ И ВЕКТОРНЫМ ПРОСТРАНСТВОМ Р^п НАД ПОЛЕМ Р

Как мы уже говорили, матрице А размером k × m можно поставить в соответствие упорядоченную систему из m вектор-столбцов в пространствеР^k, либо из к вектор-строк в пространствеР^m. Обе упорядоченные системы векторов и– есть элементы одного и того же векторного пространства Рⁿ, где n = k·m, которое и является изоморфным для векторного пространства матриц размером k×m. Действительно,

и .

Рассмотрим теперь систему, состоящую из одного вектора . Очевидно, что этот вектор через свои компоненты в пространстве матриц будет ассоциироваться с матрицами размером 1n, либо n1; матрица размером 1n; матрица размеромn1. Ясно, что отображение есть изоморфизм, ибо

Используя указанный изоморфизм, покажем, как представляется отображение , гдев пространстве матриц.

Пусть отображение А пространства Р^m в Р^k задано формулами:

_  __  __ +   +_1m_m,

₂  _2_  _2_ +   +_2m_m,

. . . . . . . . . . . . . . . . . . . . . . . . . .

_к  _k_  _{k }_ +   +_km_m .

Вектору с компонентами₁,₂, . . .,_к) из Р^k поставим в соответствие матрицу:

размером k 1, а вектору с компонентами (_ ,_,   ,_m) матрицу размеромm1. Тогда отображение, определяемое матрицей

А = размеромk×m в пространстве матриц определяется той же матрицей А и представляется в виде:

=·

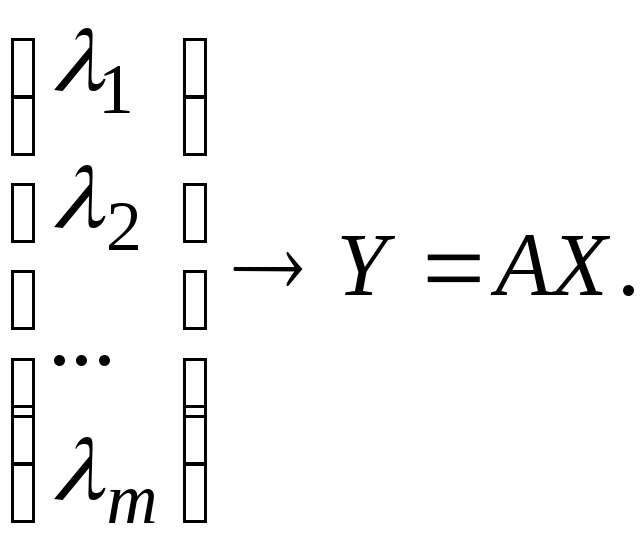
В заключение рассмотрим, как в пространстве матриц отображается скалярное произведение двух векторов из пространства .

§4. Скалярное произведение двух векторов из пространства Rn

Определение. Рассмотрим отображение φ векторного пространства RⁿRⁿ в R, при котором устанавливается следующее соответствие

,

здесь ; упорядоченная пара (), является элементом векторного пространстваRⁿRⁿ; (_ ,_,   ,_n) и (β₁, β₂, . . . , β_n) компоненты соответственно векторов ;число изR. Такое отображение  называется скалярным произведением двух векторов из пространстваRⁿ и обозначается ( , ), а само число– () либо.

Отображение  не является линейным отображением. Действительно, так как RⁿRⁿ векторное пространство, то

. Легко показать, что и, следовательно, отображение не является линейным отображением.

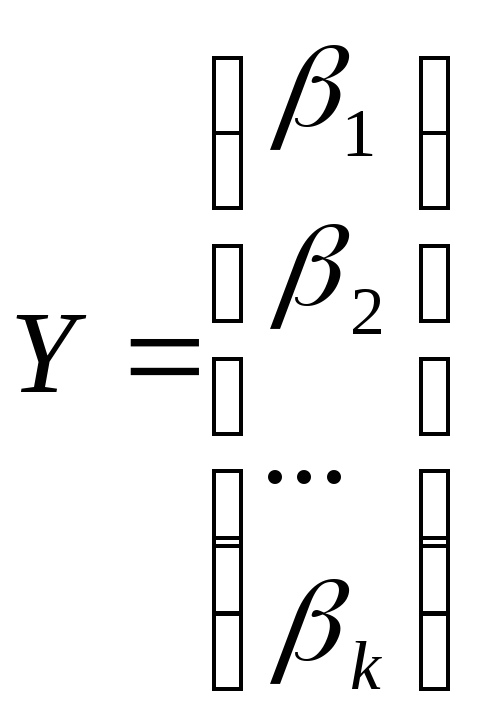Выясним теперь, как скалярное произведение представляется в пространстве матриц. Пусть даны два вектора Теперь векторупоставим в соответствие матрицуразмером 1n, а вектору – матрицу размеромn1. Тогда произведение в пространстве матриц эквивалентно произведению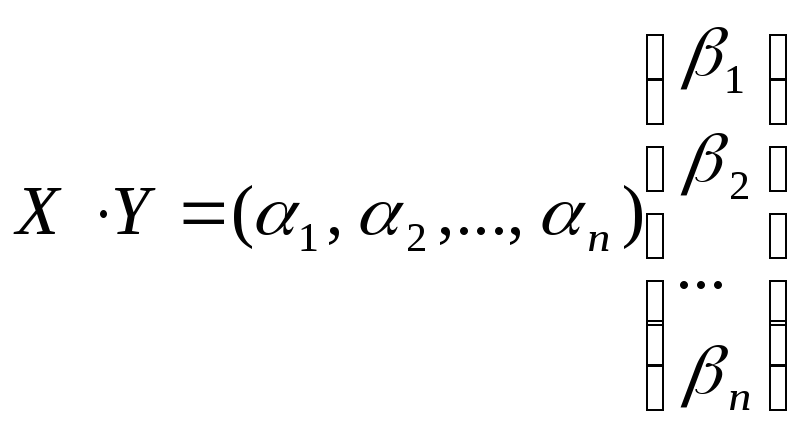=₁₁₂₂  . . .  _n_n.

Видно, что и в векторном пространстве матриц отображение  не является линейным отображением

§5. Квадратные матрицы

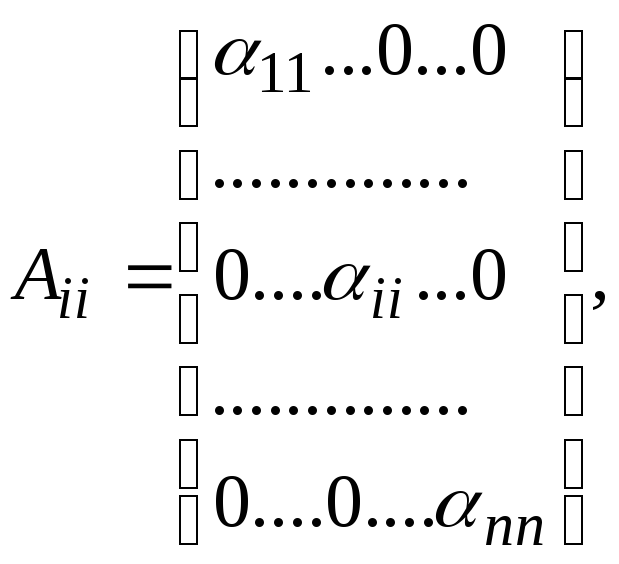
Определение. Матрица, у которой число строк равно числу столбцов, называется квадратной; одинаковое число n строк и столбцов называется порядком матрицы.

Множество элементов _ii называется главной диагональю, а матрица, у которой все элементы, расположенные вне главной диагонали есть нули _ij = 0, если i  j, называется диагональной. если все элементы диагональной матрицы одинаковы_ii = , то такая матрица называется скалярной.

Диагональная матрица, все элементы которой равны единице, называется единичной и обозначается Е_n (или I_n).

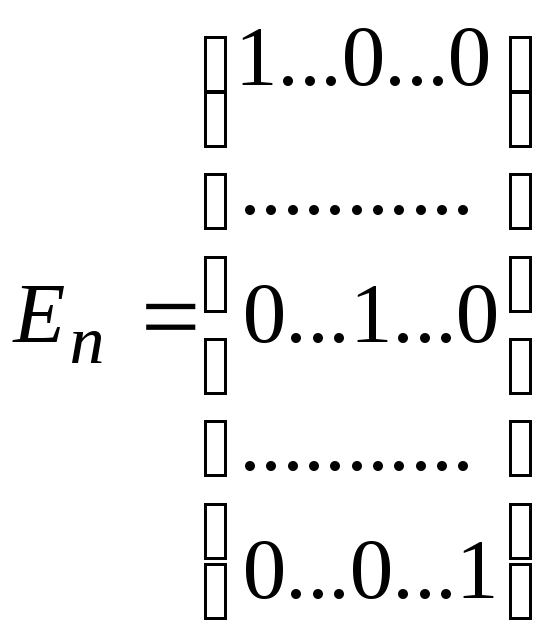или E_n = (_ij ), где i = 1,2,...,n; j = 1,2,...,n;  _ij – символ Кронекера. Единичная матрица E_n представляет собой нейтральный элемент относительно умножения матриц А порядка n: АE_n = E_nА = А.

Сумма и произведение двух матриц n-го порядка всегда определены и результатом будут матрицы порядка n. Однако произведение квадратных матриц не коммутативно: А·В  В·А. Например,

Квадратные матрицы порядка n определяют линейные отображения Рⁿ в Рⁿ, а единичная матрица E_n ассоциируется с системой векторов канонического базиса пространстваРⁿ.