
- •Линейная алгебра глава 1 законы композиции
- •§1. Внутренние законы композиции
- •1.2. Основные алгебраические образования: группы, кольца, поля
- •§2. Внешние законы композиции
- •§3. Изоморфизм
- •Глава 2 комплексные числа
- •§1. Поле с комплексных чисел
- •Потренироваться в сложении-вычитании и умножении
- •§2. Комплексно сопряженные числа
- •§3. Модуль комплексного числа. Деление двух комплексных чисел
- •§4. Геометрическая интерпретация комплексных чисел
- •§5. Тригонометрическая форма комплексного числа. Формула муавра. Извлечение корня
- •§6. Комплексные функции
- •Комплексные функции одного действительного переменного
- •Показательная функция zеz с комплексным показателем и ее свойства
- •Формулы Эйлера. Показательная форма комплексного числа
- •Глава 3 многочлены
- •§1. Кольцо многочленов
- •§2. Деление многочленов по убывающим степеням
- •§3. Взаимно простые и неприводимые многочлены. Теорема и алгоритм евклида
- •§4. Нули (корни) многочлена. Кратность нуля. Разложение многочлена в произведение неприводимых многочленов над полем с и r
- •Упражнения
- •Глава 4 векторные пространства
- •§1. Векторное пространство многочленов над полем p коэффициентов
- •§2. Векторные пространства р n над полем р
- •§3. Векторы в геометрическом пространстве
- •3.1. Типы векторов в геометрическом пространстве
- •Из подобия треугольников авс и ав'с' следует (как в случае , так и в случае ), что.
- •3.3. Задание свободных векторов при помощи декартовой системы координат и соответствие их с векторами из векторного пространства r3
- •3.4. Скалярное произведение двух свободных векторов
- •Упражнения
- •§4. Векторное подпространство
- •4.1. Подпространство, порожденное линейной комбинацией векторов
- •4.2. Линейная зависимость и независимость векторов
- •4.3. Теоремы о линейно зависимых и линейно независимых векторах
- •4.4. База и ранг системы векторов. Базис и размерность векторного подпространства, порожденного системой векторов
- •4.5. Базис и размерность подпространства, порожденного системой
- •§5. Базис и размерность векторного пространства
- •5.1. Построение базиса
- •5.2. Основные свойства базиса
- •5.3. Базис и размерность пространства свободных векторов
- •§6. Изоморфизм между n – мерными векторными пространствами к и р n над полем р
- •§8. Линейные отображения векторных пространств
- •8.1. Ранг линейного отображения
- •8.2. Координатная запись линейных отображений
- •Упражнения
- •Глава 5 матрицы
- •§1. Ранг матрицы. Элементарные преобразования матриц
- •§2. Алгебраичесие операции над матрицами.
- •Пусть даны матрицы
- •§3. Изоморфизм между векторным пространством
- •§4. Скалярное произведение двух векторов из пространства Rn
- •§5. Квадратные матрицы
- •5.1. Обратная матрица
- •5.2. Транспонированная квадратная матрица.
- •Упражнения
- •Глава 6 определители
- •§1. Определение и свойства определителя, вытекающие из определения
- •§2. Разложение определителя по элементам столбца (строки). Теорема о чужих дополнениях
- •§3. Геометрическое представление определителя
- •3.1. Векторное произведение двух свободных векторов
- •3.2. Смешанное произведение трех свободных векторов
- •§4. Применение определителей для нахождения ранга матриц
- •§5. Построение обратной матрицы
- •Упражнения
- •Глава 7 системы линейных уравнений
- •§1. Определения. Совместные и несовместные системы
- •§2. Метод гаусса
- •§3. Матричная и векторная формы записи линейных
- •3. Матрицу-столбец свободных членов размер матрицыk 1.
- •§4. Система крамера
- •§5. Однородная система линейных уравнений
- •§6. Неоднородная система линейных уравнений
- •Упражнения
- •Глава 8 приведение матриц
- •§1. Матрица перехода от одного базиса к другому
- •1.1. Матрица перехода, связанная с преобразованием
- •1.2. Ортогональные матрицы перехода
- •§2. Изменение матрицы линейного отображения при замене базисов
- •2.1. Собственные значения, собственные векторы
- •2.2. Приведение квадратной матрицы к диагональной форме
- •§3. Вещественные линейные и квадратичные формы
- •3.1. Приведение квадратичной формы к каноническому виду
- •3.2. Определенная квадратичная форма. Критерий Сильвестра
- •Упражнения (номера с 1465 и далее)
Из подобия треугольников авс и ав'с' следует (как в случае , так и в случае ), что.
Но
![]() ,
следовательно
,
следовательно![]() .
.
Из
доказательства свойства 4 вытекает
следующее условие
компланарности
векторов. Для того чтобы три вектора
![]() ,
,![]() и
и![]() были
компланарны, необходимо и достаточно,
чтобы они удовлетворяли соотношению
были
компланарны, необходимо и достаточно,
чтобы они удовлетворяли соотношению![]() ,
гдеR
и R.
Это соотношение читается так: вектор
,
гдеR
и R.
Это соотношение читается так: вектор
![]() естьлинейная
комбинация
векторов
естьлинейная
комбинация
векторов
![]() и
и![]() .
.
Таким образом, множество свободных векторов, на котором заданы данные операции сложения векторов и умножение вектора на число из R, образует векторное пространство над полем R.
Теперь рассмотрим, как можно задать вектора с помощью декартовой прямоугольной системой координат, и установим их соответствие с векторами из пространства R3.
3.3. Задание свободных векторов при помощи декартовой системы координат и соответствие их с векторами из векторного пространства r3
Выберем
в пространстве декартовую прямоугольную
систему координат x,
y,
z. Рассмотрим
произвольный вектор
![]() ,
который задан направленным отрезком
,
который задан направленным отрезком![]() Напомним, что точкаА
может быть любой точкой пространства.
В выбранной системе координат определим
координаты начала вектора – точки А
и конца этого вектора – точки В
(рис.2.4).
Напомним, что точкаА
может быть любой точкой пространства.
В выбранной системе координат определим
координаты начала вектора – точки А
и конца этого вектора – точки В
(рис.2.4).
Пусть
координатами точки А
является тройка чисел (х1,
у1,
z1),
а точки В
– (х2,
у2,
z2).
Тогда координатами вектора
![]() называют упорядоченную тройку чисел
(х,
у,
z), вычисляемые
по формулам:
называют упорядоченную тройку чисел
(х,
у,
z), вычисляемые
по формулам:
х = х2 – х1; у = у2 – у1; z = z2 – z1, (рис.2.4)
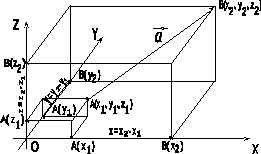
Рис. 2.4
Записывают
это таким образом
![]() (х,
у,
z)
или
(х,
у,
z)
или
![]() (ах,
ау,
аz).
(ах,
ау,
аz).
Если
начало направленного отрезка
![]() совпадает с началом координатА(х1,
у1,
z1)
= О (0, 0, 0,), то
направленный отрезок называется
радиус-вектором точки В.
В этом случае координаты (х,
у,
z), вектора
совпадает с началом координатА(х1,
у1,
z1)
= О (0, 0, 0,), то
направленный отрезок называется
радиус-вектором точки В.
В этом случае координаты (х,
у,
z), вектора
![]() совпадают с координатамих2,
у2,
z2
точки В:
х = х2,
у = у2,
z = z2.
совпадают с координатамих2,
у2,
z2
точки В:
х = х2,
у = у2,
z = z2.
Таким
образом, выбрав в пространстве декартову
систему координат, мы с ее помощью можем
установить соответствие между любым
вектором
![]() ,
заданным направленным отрезком
,
заданным направленным отрезком![]() и вектором
и вектором![]() из векторного пространстваR3,
координаты которого определяются
упорядоченной тройкой чисел (х,
у,
z).
Если указанное соответствие, представляющее
собой способ нахождения координат
методом проектирования, обозначить
через f,
то
из векторного пространстваR3,
координаты которого определяются
упорядоченной тройкой чисел (х,
у,
z).
Если указанное соответствие, представляющее
собой способ нахождения координат
методом проектирования, обозначить
через f,
то
f
:![]()
![]() =f
(
=f
(![]() )
= (х,
у,
z).
)
= (х,
у,
z).
Покажем, что f является взаимно однозначным отображением. Для этого рассмотрим теорему о равенстве векторов.
Теорема. Два вектора равны тогда и только тогда, когда равны их координаты.
Для
доказательства этой теоремы вначале
покажем, как можно задать вектор
![]() при помощи его длины
при помощи его длины![]()
и углов, которые он образует с координатными
осями.
и углов, которые он образует с координатными
осями.
Рассмотрим
произвольный направленный отрезок
![]() ,
принадлежащий множеству вектора
,
принадлежащий множеству вектора![]() .
Построим на
.
Построим на![]() ,
как на диагонали, прямоугольный
параллелепипед (рис.2.5) со сторонамиАА1
= х
= х2
– х1
= ах;
АА2
= у = у2
–
у1
= ау;
АА3
= z = z2
– z1
= аz
.
,
как на диагонали, прямоугольный
параллелепипед (рис.2.5) со сторонамиАА1
= х
= х2
– х1
= ах;
АА2
= у = у2
–
у1
= ау;
АА3
= z = z2
– z1
= аz
.




![]()
Рис. 2.5.
Заметим, что все точки, лежащие на плоскости, параллельной какой-либо координатной плоскости, имеют равные координаты той оси, к которой эта плоскость перпендикулярна. Если точки расположены на прямой, параллельной какой-либо из координатных осей, то для этих точек изменяется только координата той оси, которой эта прямая параллельна. Две другие координаты одинаковы. Например, точки А и А1 (рис.2.5) лежат на прямой, параллельной оси Ох, следовательно, для этих точек изменяется только координата х.
Теперь
обозначим через ,
и
углы, которые образует направленный
отрезок
![]() с осями координатx,
y,
z соответственно
или со сторонами параллелепипеда АА1,
АА2,
АА3
(рис.2.5). Из
прямоугольных треугольников АА1В,
АА2В
и АА3В
находим
с осями координатx,
y,
z соответственно
или со сторонами параллелепипеда АА1,
АА2,
АА3
(рис.2.5). Из
прямоугольных треугольников АА1В,
АА2В
и АА3В
находим
х
= х2
– х1
= ах
=![]()
cos,
cos,
у
= у2
– у2
=ау
= ![]()
cos,
(
4.2 )
cos,
(
4.2 )
z
= z2
– z1
= az
= ![]()
cos,
cos,
где
![]()
=
= ![]()
=
=![]() ,
,
cos, cos и cos называются направляющими косинусами, и для них имеет место соотношение
cos2 + cos2 + cos2 = 1. ( 4.3)
Теперь на основании полученных формул
докажем теорему равенства векторов.
Рассмотрим два вектора
![]() и
и![]() с координатами соответственноx1,y1,z1
и x2,y2,z2.
с координатами соответственноx1,y1,z1
и x2,y2,z2.
Необходимость.
Покажем, что если векторы равны (![]() =
=![]() ),
то и их координаты тоже равны (x1
= x2;
y1
= y2;
z1
= z2).
Из равенства векторов следует, что
),
то и их координаты тоже равны (x1
= x2;
y1
= y2;
z1
= z2).
Из равенства векторов следует, что ![]()
=
= ![]() ,
а также, что cos
cos,
cos
= cos,
cos
= cos,
так как векторы коллинеарны и одинаково
направлены. Если бы векторы были
коллинеарны и противоположно направлены,
то cos
– cos,
cos
= – cos,
cos
= – cos.
Теперь из формул (4.2) следует:
,
а также, что cos
cos,
cos
= cos,
cos
= cos,
так как векторы коллинеарны и одинаково
направлены. Если бы векторы были
коллинеарны и противоположно направлены,
то cos
– cos,
cos
= – cos,
cos
= – cos.
Теперь из формул (4.2) следует:
x1
=![]()
cos
=
cos
= ![]()
cos
= х2,
cos
= х2,
у1
=![]()
cos
=
cos
= ![]()
cos
= у2,
cos
= у2,
z1
=![]()
cos
=
cos
= ![]()
cos
= z2,
cos
= z2,
что и требовалось доказать.
Достаточность.
Так как координаты векторов
![]() и
и![]() равны, то
равны, то
![]() =
=
![]()
и
cos
= cos,
cos
= cos,
cos
= cos.
и
cos
= cos,
cos
= cos,
cos
= cos.
Второе
условие означает, что векторы
![]() и
и![]() коллинеарны и направлены в одну сторону,
а с учетом
коллинеарны и направлены в одну сторону,
а с учетом![]()
=
= ![]()
такие вектора считаются равными, т.е.
такие вектора считаются равными, т.е.
![]() =
=![]() .
.
. Из
теоремы равенства векторов непосредственно
следует, что отображение
![]()
![]() = (x,y,z)
является взаимно однозначным.
Действительно, каждому вектору
= (x,y,z)
является взаимно однозначным.
Действительно, каждому вектору
![]() из векторного пространства свободных
векторов можно поставить в соответствие
единственный вектор
из векторного пространства свободных
векторов можно поставить в соответствие
единственный вектор![]() = (x,y,z)
из векторного пространства R3
и наоборот,
каждой упорядоченной тройке чисел
(x,y,z),
т.е. вектору из R3
, можно поставить в соответствие
единственный вектор
= (x,y,z)
из векторного пространства R3
и наоборот,
каждой упорядоченной тройке чисел
(x,y,z),
т.е. вектору из R3
, можно поставить в соответствие
единственный вектор
![]() из векторного пространства свободных
векторов. Для построения этого вектора
достаточно построить радиус-вектор
точкиВ(x,y,z)
в выбранной системе координат. Тогда
множество всех направленных отрезков,
равных направленному отрезку
из векторного пространства свободных
векторов. Для построения этого вектора
достаточно построить радиус-вектор
точкиВ(x,y,z)
в выбранной системе координат. Тогда
множество всех направленных отрезков,
равных направленному отрезку
![]() и является вектором
и является вектором![]() с координатамиx,y,z.
Отметим, что это соответствие зависит
от выбора системы координат.
с координатамиx,y,z.
Отметим, что это соответствие зависит
от выбора системы координат.
Если
вектор
![]() расположен в одной из координатных
плоскостей, то одна из координат равна
нулю, например, если эта плоскостьхОу,
то координата z = 0.
Изображать такой вектор можно направленным
отрезком, лежащим в любой из плоскостей,
параллельной плоскости
хОу. В этом
случае каждому вектору
расположен в одной из координатных
плоскостей, то одна из координат равна
нулю, например, если эта плоскостьхОу,
то координата z = 0.
Изображать такой вектор можно направленным
отрезком, лежащим в любой из плоскостей,
параллельной плоскости
хОу. В этом
случае каждому вектору ![]() ,
расположенному в координатной плоскости,
можно поставить в соответствие
упорядоченную пару чисел (х,у),
представляющую собой вектор из векторного
пространства R2
и это соответствие взаимно однозначно.
,
расположенному в координатной плоскости,
можно поставить в соответствие
упорядоченную пару чисел (х,у),
представляющую собой вектор из векторного
пространства R2
и это соответствие взаимно однозначно.
Если
вектор
![]() расположен на одной из координатных
осей, то остальные две его координаты
равны нулю и поэтому каждому вектору
расположен на одной из координатных
осей, то остальные две его координаты
равны нулю и поэтому каждому вектору![]() ,
расположенному на координатной оси,
можно поставить в соответствие вектор
с координатойх
из векторного пространства R1
и это соответствие взаимно однозначно.
Изображать такой вектор можно направленным
отрезком, расположенным на любой прямой,
параллельной соответствующей координатной
оси.
,
расположенному на координатной оси,
можно поставить в соответствие вектор
с координатойх
из векторного пространства R1
и это соответствие взаимно однозначно.
Изображать такой вектор можно направленным
отрезком, расположенным на любой прямой,
параллельной соответствующей координатной
оси.
Покажем теперь, что операции сложения свободных векторов и умножение их на число из поля R находятся в полном соответствии с аналогичными операциями над векторами из R3, т.е. относительно данных операций эти пространства изоморфны. Перечислим эти операции без доказательства, так как все они доказаны в курсе средней школы.
Сумма свободных векторов. Координаты суммы двух свободных векторов равны суммам соответствующих координат слагаемых.
На
координатной оси:
![]() (х1)
и
(х1)
и
![]() (х2);
(х2);
![]() (х1)
+
(х1)
+
![]() (х2)
=
(х2)
=
![]() (х1
+ х2).
(х1
+ х2).
На
координатной плоскости :
![]() (х1,у1)
и
(х1,у1)
и
![]() (х2,у2);
(х2,у2);
![]() (х1,у1)
+
(х1,у1)
+
![]() (х2,у2)
=
(х2,у2)
=
![]() (х1
+ х2,
у1
+ у2).
(х1
+ х2,
у1
+ у2).
В
пространстве:
![]() (х1,у1,z1)
и
(х1,у1,z1)
и
![]() (х2,у2,z2);
(х2,у2,z2);
![]() (х1,у1,z1)
+
(х1,у1,z1)
+
![]() (х2,у2,z2)
=
(х2,у2,z2)
=
![]() (х1
+ х2,
у1
+ у2,
z1
+ z2)
– соответствие см. формулу (4.1).
(х1
+ х2,
у1
+ у2,
z1
+ z2)
– соответствие см. формулу (4.1).
Умножение
свободного вектора на число из поля R.
Координаты
произведения
![]() вектора
вектора![]() (x,y,z)
на число
равны произведениям этого числа на
соответствующие координаты вектора
(x,y,z)
на число
равны произведениям этого числа на
соответствующие координаты вектора
![]() .
.
![]() )
– соответствие см. формулу (4.1).
)
– соответствие см. формулу (4.1).
Следствие.
Для того чтобы два вектора
![]() (х1,у1,z1)
и
(х1,у1,z1)
и
![]() (х2,у2,z2)
были коллинеарны, т.е.
(х2,у2,z2)
были коллинеарны, т.е.
![]() ,
необходимо и достаточно, чтобы
соответствующие координаты векторов
были пропорциональны:
,
необходимо и достаточно, чтобы
соответствующие координаты векторов
были пропорциональны:![]() .
.
Кроме этих двух операций введем еще одну операцию над свободными векторами, с которой вы познакомились в курсе средней школы, но смысл, которой мы раскроем чуть позже.
