Упражнения

1. Доказать, что операция пересечения множеств дистрибутивна относительно операции объединения множеств.

2. Является ли множество Q рациональных чисел, на котором задана операция умножения группой?

3. Является ли множество Q полем, если:

а) на этом множестве в качестве первого закона задан закон умножения, а второй – сложение?

б) первый закон – сложение, второй – умножение?

2. Вычислить

3. Найти действительные значения х и у из уравнения

(1 + i) x² + (2 + i) x – (1 – i) y = 7(1 + i).

2. Какой геометрический смысл имеет модуль разности двух комплексных чисел? Определить этот модуль для z = 3 + i2 и . Изобразить эти точки на комплексной плоскости.

3. Найти все корни и построить их на комплексной плоскости:

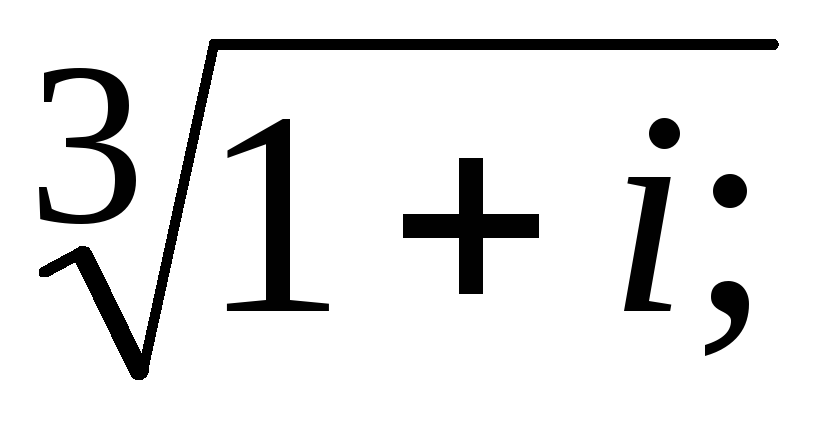
4. Решить уравнения:

а) 2x² – 3x + 7 = 0, б) cos x = 3, в) sin x = 2.

2. Найти корни уравнения z⁸ – 2z⁴ + 4 = 0 и построить их на комплексной плоскости.

3. Представить в показательной форме комплексные числа:

1 + i, –1 + i, –5, + i.

2. Разделить многочлен 3х⁶ + 2х³ – 2х + 5 на многочлен 2х² + 3 по убывающим степеням.

3. Определить кратность нуля х = 1 для многочлена

f (x) = 3х⁵ – 8х⁴ +4х³ + 6х² – 7х + 2

и представить разложение этого многочлена в произведение неприводимых многочленов на поле R и С.

Глава 4 векторные пространства

На некотором множестве К, наделенном внутренним законом коммутативной группы, может быть определен также при помощи некоторого другого множества L, внешний закон композиции – отображение KL в К. Наиболее важным множеством такого типа является векторное пространство (или линейное пространство).

Определение. Множество К называется векторным (линейным) пространством над полем Р, если оно наделено внутренним законом (+) – сложение и внешним законом (·) – умножение на элемент из поля Р, обладающих следующими свойствами:

1. Сложение на множестве К наделено внутренним законом коммутативной группы. х  у и  z имеем:

х + у = у + х;

х + (у + z) = (х + у) + z;

 е   такой, что х + е = е + х = х (нейтральный элемент),

такой что (симметричный элемент).

2. Внешний закон умножения, таким что  х, у и ,  ,

х + у) =  х +  у

(    х =  х   х

 х) = ( х

 х = х,

где  есть нейтральный элемент умножения в поле Р.

Элементы из векторного пространства К называются векторами и обычно обозначаются строчными латинскими буквами со стрелками вверху (и т.п.) или же строчными буквами выделенными жирным шрифтом (a, в, x и т.п.). Элементы поля Р чаще всего обозначаются строчными греческими буквами (и т.п.). Нейтральный элемент сложенияе в К называется нулевым вектором и обозначается . Нейтральный элемент сложенияе в Р обозначается 0 (нулем), а умножения  – 1 (единица). Элемент симметричныйх называется также противоположным вектору и обозначается, т.е..

Следствия из определения. 1) В векторном пространстве может быть только один нулевой вектор и для каждого вектора только один противоположный. Действительно, допустим, что существуют два нулевых вектора итогда из определения следует, что их сумма должна быть равна каждому из них, т.е., илии, следовательно,Аналогично, если какой-нибудь векторимеет два противоположныхи, то суммадолжна быть равна ии, следовательно=.

2) Если то либо, либо .

3) Равенство выполнено для любых и  если. Если же, то, прибавив к обеим частям равенстваполучим,и значит, но, следовательно –    и   .

4) Равенство выполнено для любыхиесли   Если же   , то или. Так как  , то откуда.