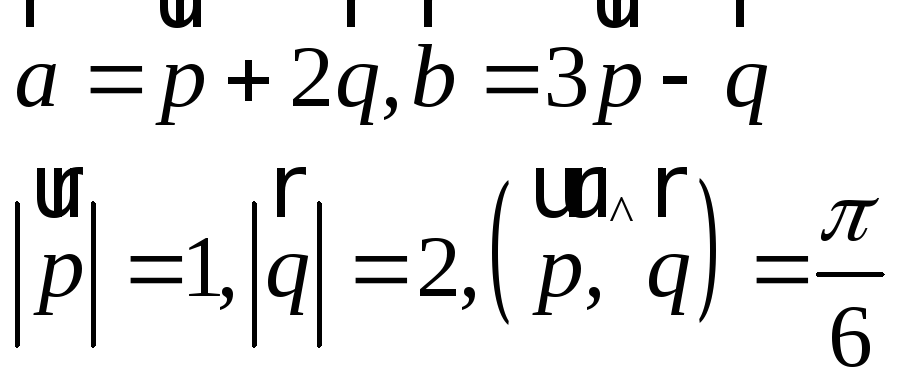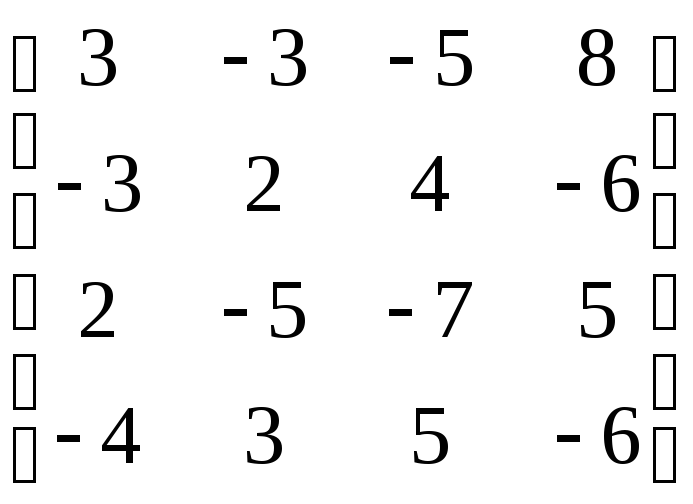Задание для практики MathCAD

5.3. Найти некоторый базис системы векторов, и все векторы, которые не принадлежат этому базису, выразить через векторы базиса:

5.3.1		5.3.2
5.3.3		5.3.4
5.3.5		5.3.6
5.3.7		5.3.8
5.3.9		5.3.10

5.4. Найти систему линейных уравнений, которая задает подпространство, порожденное системой векторов:

5.4.1		5.4.2
5.4.3		5.4.4
5.4.5		5.4.6
5.4.7		5.4.8
5.4.9		5.4.10

5.5. Коллинеарные ли векторы и , построенные по векторам и ?

5.5.1		5.5.2
5.5.3		5.5.4
5.5.5		5.5.6
5.5.7		5.5.8
5.5.9		5.5.10

5.6. Векторы и взаимно перпендикулярны, вектор образует с ними углы равные . Если , вычислить следующие скалярные произведения:

5.6.1		5.6.2
5.6.3		5.6.4
5.6.5

5.7. В декартовой прямоугольной системе координат заданы векторы . Найти скалярное произведение:

5.7.1		5.7.2
5.7.3		5.7.4
5.7.5

5.8. Найти косинус угла между векторами и , если:

5.8.1		5.8.2
5.8.3		5.8.4
5.8.5		5.8.6
5.8.7		5.8.8
5.8.9		5.8.10

5.9. Нормировать векторы и вычислить угол между ними

5.9.1

5.9.2

5.10. Вычислить проекцию вектора на вектор

5.10.1		5.10.2
5.10.3		5.10.4
5.10.5		5.10.6

5.11. Вычислить площадь параллелограмма, построенного на векторах и .

5.11.1		5.11.2
5.11.3		5.11.4
5.11.5		5.11.6
5.11.7		5.11.8
5.11.9		5.11.10
5.11.11

5.12.Найти площадь треугольника, если даны координаты его вершин и длину его высоты, опущенной из вершины В

5.12.1

5.12.2

5.13. Даны векторы . Найти координаты векторного произведения векторов:

5.13.1		5.13.2
5.13.3		5.13.4
5.13.5

5.14. Векторы и образуют угол . Вычислить:

5.14.1		5.14.2
5.14.3		5.14.4
5.14.5

5.15. Вычислить смешанное произведение векторов :

5.15.1		5.15.2
5.15.3		5.15.4
5.15.5		5.15.6
5.15.7		5.15.8
5.15.9		5.15.10

5.16. Компланарны ли векторы , и ?

5.16.1		5.16.2
5.16.3		5.16.4
5.16.5		5.16.6
5.16.7		5.16.8
5.16.9		5.16.10
5.16.11		5.16.12

5.17. Вычислить объем тетраэдра с вершинами в точках и его высоту, опущенную из вершины на грань , если:

5.17.1		5.17.2
5.17.3		5.17.4
5.17.5		5.17.6
5.17.7		5.17.8
5.17.9		5.17.10

5.18. Найти проекцию вектора , на плоскость векторов и , если

5.18.1

5.19. Найти проекции вектора на вектор и на вектор если

5.19.1

5.20. Нормировать векторы и и вычислить угол между ними, если

5.20.1

5.20.2

Задание №6

Матрицы

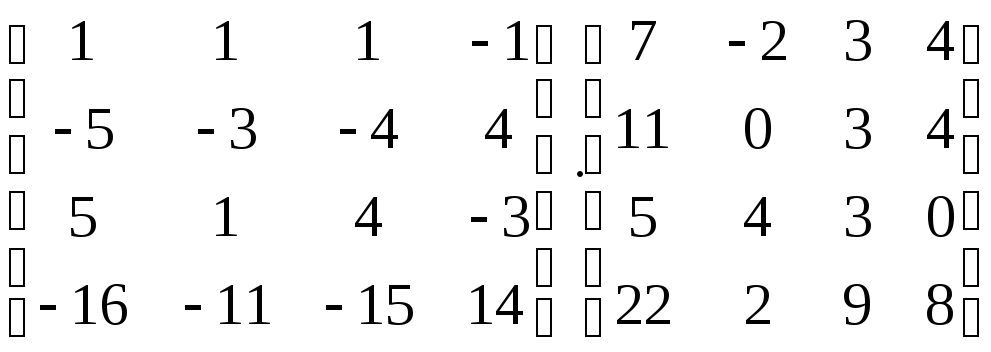
6.1. Вычислить произведение матриц

6.1.1		6.1.2
6.1.3		6.1.4
6.1.5		6.1.6
6.1.7		6.1.8
6.1.9		6.1.10

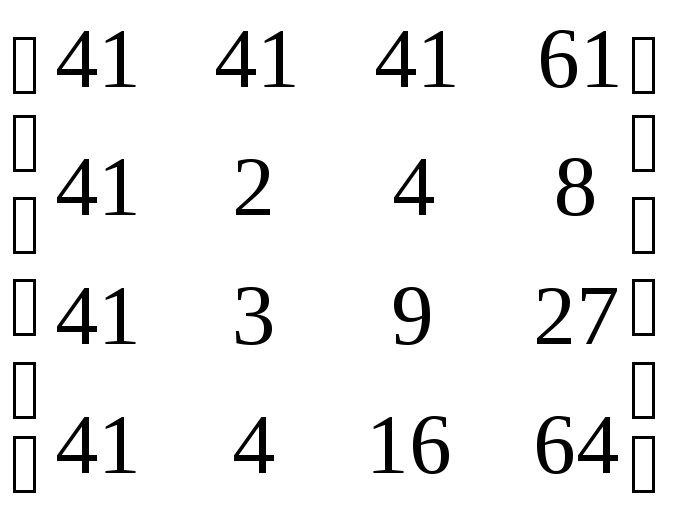
6.2. Вычислить определители следующих матриц

6.2.1		6.2.2
6.2.3		6.2.4
6.2.5		6.2.6
6.2.7		6.2.8
6.2.9		6.2.10
6.2.11		6.2.12
6.2.13		6.2.14
6.2.15		6.2.16
6.2.17		6.2.18
6.2.19		6.2.20
6.2.21		6.2.22
6.2.23		6.2.24
6.2.25		6.2.26
6.2.27		6.2.28
6.2.29		6.2.30
6.2.31		6.2.32

6.3. Вычислить обратную матрицу для следующих матриц

6.3.1		6.3.2
6.3.3		6.3.4
6.3.5		6.3.6
6.3.7		6.3.8
6.3.9		6.3.10
6.3.11		6.3.12
6.3.13		6.3.14
6.3.15		6.3.16
6.3.17		6.3.18

6.4. Определить ранг матрицы

6.4.1		6.4.2
6.4.3		6.4.4
6.4.5		6.4.6
6.4.7		6.4.8
6.4.9		6.4.10
6.4.11		6.4.12
6.4.13		6.4.14
6.4.15		6.4.16