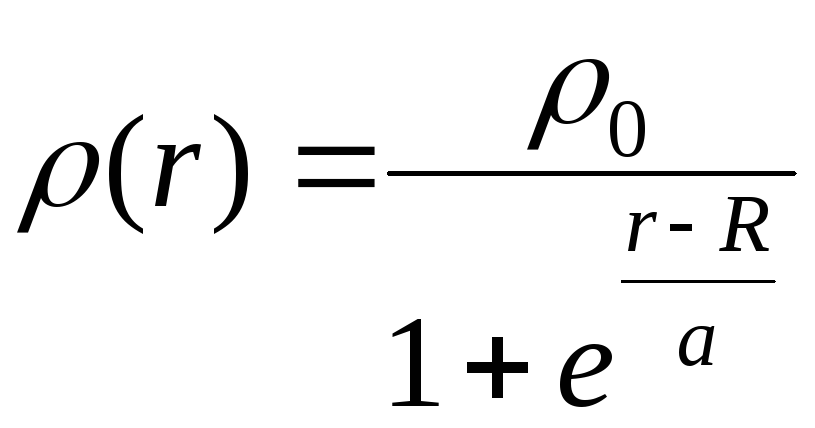ядерка
.doc|
1. Масштабы ядер-х явлений, особенности ядерных явлений. R~1013см – характер-я длина. Характерное время считается tN=R/C, время в течение которого час-ца движется со скоростью света проходят через ядро. tN~10-23с. Энергия. 1эВ=1,6*10-12эрг. 1МэВ=106эВ. Особенности ядерных явлений: 1.
Проявление релятивиствких свойств
скорости,V~c=3*1010cм/с.E=
|
2.1.Структура ядра. Ядро состоит из элементарных частиц, протонов и нейтронов. Протон электрически заряжен(+) и по абсолютной величине равен заряду электрона. В отличие от электронов p и n подвержены действию специфических ядер.сил. Яд.силы являются частным случаемсамых интенсивных в природе сильных взаимодействий. За счет ядерных сил p и n соединятся друг с другом, образуя различные атомные ядра. Атом электрически нейтрален. Поэтому число протонов = числу электронов в атомной оболочке, т.е. атомному номеру Z. Общее число нуклонов в ядре обозначается А и наз. атомным числом. N-число нейтронов в ядре. Ядра с одним и тем же Z и равными A называются изотопами. Изобары – ядра с одинаковыми А и разными Z. Изотоны – одинаковые N и разные Z. Атомные ядра состоят из элементарных частиц: протонов, нейтронов. Это связано с тем, что их свойства близки по отношению к сильному взаимодействию. Протон
Обозначается “p”,
открыт в 1919 году Резерфордом. |
2.2В
ядерной физике говорят, что протон и
нейтрон образуют изотопический дублет.
С точки зрения сильного взаимодействия,
взаимодействия вида n-n,n-p,p-p
неразличимы. Данное свойство называется
изотопическая инвариантность ядерных
сил. Из-за наличия протона и нейтрона
атомные ядра получили определенные
символы для обозначения: Z
- число протонов, N
- число нейтронов, A=Z+N
- массовое число. Атомные ядра
обозначаются следующим образом:
Ядра
с одинаковыми массовыми числами, но
разными числами Z
называются изобары.
Пример:
Ядра с одинаковыми N, но разными Z называются изотоны. Существуют частные случаи изобарных ядер - зеркальные ядра. В зеркальных ядрах: Z1=N2 , Z2=N1.Пример: Химические свойства атомов определяется числом Z, массовое число A влияет на химические и физические свойства ядра, атомные ядра могут существовать в определенном диапазоне чисел A, Z, за пределами которого ядра распадаются и являются - нестабильными. Для определения этого диапазона вводят понятие энергия связи.
|
3.1. Формула Мота Рассмотрим упругое рассеяние электронов на ядре и покажем, как из экспериментальных данных можно извлечь сведения о пространственной структуре ядра-мишени. Упругое рассеяние означает, что не происходит изменения внутреннего состояния ядра после рассеяния. Оно не возбуждается. Прежде всего рассмотрим рассеяние электронов на точечном (бесструктурном) и бесспиновом ядре. Рассеяние на точечном объекте, естественно, всегда только упругое. Для дифференциального сечения рассеяния должна иметь место формула наподобие формулы Резерфорда. Однако эта формула должна отличаться от формулы Резерфорда в двух отношениях: 1. Она должна быть применима к релятивистским частицам (vc); 2. Она должна учитывать наличие ненулевого спина (1/2) у электрона. Такая формула была получена Моттом в 1929 г. в рамках квантовой электродинамики и в пренебрежении отдачей ядра имеет вид
Множитель cos2™/2 появляется из-за наличия спина у электрона. Формула Мотта получена в предположении бесструктурности (точечности) ядра. |
3.2Вплоть
до расстояний 10-16
см (предел, достигнутый на сегодняшний
день) у электрона не обнаружена
структура (отличие от точечности).
Таким образом, в форм-фактор упругого
рассеяния дает вклад только (r)
ядра. Схема нахождения (r)
такова. Определяют
В
свою очередь, т.к. заряд ядра создается
протонами, (r)=Ze|p( |
|
4. Распределение электрического заряда в ядрах и нуклонах.Для количественного исследования вопроса о размерах ядер вводят понятие радиуса ядра. Среднеквадратический радиус Rэл
= 0,62 Фм. ρ(r)-плотность распределения заряда. У квантовой частицы непосредственно определяемой величиной является Фурье образ F(q) плотностью ρ(r):
Выразим Rэл через F(q). Для этого введем ф-ию F0(q2), зависящую только от радиальной переменной q2.
dщ-элемент телесного угла заряда и является Фурье – образом усредненного по углам распределения плотности заряда. F(0)=Ze – полный заряд ядра, а
Опыты по рассеиванию электронов высокой энергии позволяет определить Rэл а так же с(r).
|
5.Энергия связи ядер. Энергией связи ядра называется энергия, необходимая для полного расщепления ядра на отдельные p и n. Вместо энергии связи удобно использовать величину Есв/А называемой удельной энергией связи. Из теории относительности следует что масса М и полная энергия связаны соотношением Е=Мс2. С помощью этого соотношения энергия связи ядра можно выразить:
Масса ядра на величину Есв/с2 меньше сумм масс нуклонов, составляющих ядро. Ядерные электронные связи часто измеряют в а.е.м. а.е.м.=1/2 массы атома углерода. Разность между массой ядра в а.е.м. и его массовым числом называется дефектом массы ядра. ∆p=0,007276 а.е.м. ∆n=0/008665 а.е.м. Если отбросить самые легкие ядра то грубо можно сказать что удельная энергия связи постоянна и приблизительно равна 8МэВ/нк. Приближенная независимость удельной энергии связи от числа нуклонов свидетельствует о свойстве насыщения ядерных сил, т.е. каждый нуклон может взаимодействовать только с нескольким соседними нуклонами. Для наиболее тяжелых ядер выгоден процесс деления на осколки идущий с выделением энергии называемой атомной.
|
6. Ф-ла Вайцзеккера для эн. связи ядер. Капельн. модель В капельной модели ядро рассматривается как сферическая капля несжимаемой заряженной ядерной жидкости радиуса R = r0A1/3. То есть в энергии связи ядра учитываются объемная, поверхностная и кулоновская энергии. Дополнительно учитываются выходящие за рамки чисто капельных представлений энергия симметрии и энергия спаривания. В рамках этой модели можно получить полуэмпирическую формулу Вайцзеккера для энергии связи ядра. Eсв(A,Z) = a1A - a2A2/3 - a3Z2/A1/3 - a4(A/2 - Z)2/A + a5A-3/4. Первое слагаемое в энергии связи ядра, подобного жидкой капле, пропорционально массовому числу A и описывает примерное постоянство удельной энергии связи ядер. Второе слагаемое - поверхностная энергия ядра уменьшает полную энергию связи, так как нуклоны, находящиеся на поверхности имеют меньше связей, чем частицы внутри ядра. Это аналог поверхностного натяжения. Третье слагаемое в энергии связи обусловлено кулоновским взаимодействием протонов. В капельной модели предполагается, что электрический заряд протонов равномерно распределен внутри сферы радиуса R = r0A1/3. Четвертое слагаемое - энергия симметрии ядра отражает тенденцию к стабильности ядер с N = Z. Пятое слагаемое - энергия спаривания учитывает повышенную стабильность основных состояний ядер с четным числом протонов и/или нейтронов.
|
7.Квантовые числа ядер m, l, n, s. n - определяет энергию, l – движется в ц.п.→ момент имп. сохран-ся. С сохраняющ. величин. связаны кв. числа. L – момент импульса <L, H>=0. Любая сохран. величина связана с симметрией => поиск сохр. величин – поиск симметрии. li – момент импульса i-той частицы, входящей в состав ядра (орбит. момент импульса). Si – внутр. момент импульса (спин i-того нуклона). Момент – величина аддитивная. Полный орбит. момент ядра: L = ∑ li . Спиновый: S = ∑ Si . Полный момент : J = L + S . ji = li + Si . J = ∑ ji . В ядре J cсохраняется . l = 0,1,2,3…;S=1/2 Если А четное, то J – целое Если А нечетное, то J –полуцелое (из-за спина)
n – определяет расположение энергетических уровней при одном и том же l.
|
8.1.Статическое электро - магнитные моменты ядер Ядро, как система зарядов и токов, обладает статическими электрическими и магнитными мультипольными моментами. Электрический дипольный момент ядра равен нулю, на основе закона сохранения четности (см. ниже). Электрические
моменты. Если
(
есть i-я компонента вектора электрического дипольного момента
есть одна из пяти линейно-независимых компонент тензора электрического квадрупольного момента. Электрический квадрупольный момент определяет взаимодействие системы с градиентом внешнего электрического поля (например, создаваемого электронной оболочкой). При наличии электрического дипольного момента возникает его взаимодействие с напряженностью внешнего электрич поля. |
|
8.2
Ядерный
спин
|
8.3собственного
магнитного момента
|
9. Альфа – распад .Альфа-распад - распад атомных ядер, сопровождающийся испусканием -частиц (ядер 4He). Часть изотопов могут самопроизвольно испускать -частицы, т.е. являются альфа-радиоактивными. Для -распада необходимо, чтобы выполненялось условие M(A,Z) > M(A-4,Z-2) + Ma , (1)где M(A,Z) и M(A-4,Z-2) - массы покоя исходного и конечного ядер соответственно, Ma - масса -частицы.Учитывая, что -распад может происходить как на возбужденные состояния конечных ядер, так и из возбужденных состояний начальных ядер, энергия -распада Qa определяется соотношением Qa = ( M(A,Z) - M(A-4,Z-2) - Ma ) с2 +Eiвоз-Efвоз, (2) где Eiвоз и Efвоз - энергии возбуждения начального и конечного ядер соответственно.Кинетическая энергия -частиц Ea связана с энергией -распада Qa соотношением Ea = QaM(A-4,Z-2)/[( M(A,Z) + Ma )][(A-4)/A]Qa , (3) Зависимость вероятности распада от энергии -частицы хорошо описывается соотношением Гейгера-Неттола lg = A lgEa + B, (4) где A и B - константы слабо зависящие от заряда ядра Z. Периоды -распада находятся в пределах от 10-7 с до 1017 лет. Такому большому диапазону периодов -распада соответствует небольшой интервал кинетических энергий -частиц от 2 до 9 МэВ. Объясняется это наличием потенциального барьера для вылетающих -частиц. |
10.
бета-распад-Распад
это самопроизвольное испускание
лептонов (e, 1.
-
(np+e-+ 2.
+
(pn+e++ 3.
e-захват
(p+e-n+ Времена -распада лежат в интервале t1/2()=0.1 сек - 1017 лет. -Распад, за который ответственны ядерные силы, может происходить за времена существенно более короткие (до 310-7 сек). На малую интенсивность слабых взаимодействий указывает и большое время жизни нейтрона (15 мин). -Распад со сравнимой энергией выделения (0.78 МэВ) идет в среднем за 10-12 сек.Энергия -распада
Qe = [M(A,Z) - M(A,Z-1) + me]c2.
|
11.1 - распад Представляет собой испускание ЭМ излучения при переходе из возбужденных состояний в более низкие энергетические состояния. В этом случае массовое число ядра не изменяется, то есть число нуклонов =const (протонов и нейтронов). В результате - распада ядро излучает - кванты (фотоны), спектр которых дискретен. Его дискретность связана с тем, что энергетические уровни ядра также дискретны. Схематично - распад можно представить следующим образом:
Энергия -
квантов
|
|
11.2Как
правило
Вероятность 2J-
мультипольного излучения определяется
величиной
Существуют следующие переходы между уровнями:
|
12.1 Законы радиоактивного распада ядер Способность ядер самопроизвольно распадаться, испуская частицы, называется радиоактивностью. Радиоактивный распад - статистический процесс. Каждое радиоактивное ядро может распасться в любой момент и закономерность наблюдается только в среднем, в случае распада достаточно большого количества ядер. Постоянной распада называется вероятность распада ядра в единицу времени л. Если в образце в момент времени t имеется N радиоактивных ядер, то количество ядер dN, распавшихся за время dt пропорционально N. dN = - л Ndt. Проинтегрировав (1) получим
Период
полураспада
T1/2
- время, за которое первоначальное
количество радиоактивных ядер
уменьшится в два раза T1/2 = ln2/
л =0.693/ л =
Активность A - среднее количество ядер распадающихся в единицу времени A(t) = л N(t). Активность измеряется в кюри (Ки) и беккерелях (Бк) |
12.2В
дальнейшем активности как первого
так и второго изотопов будут изменяться
во времени одинаково. ) A1(t) = N10(t)
л 1
|
13.Ядерные реакции. Любой процесс столкновения элементарной частицы с ядром или ядра с ядром будем называть ядерной реакцией. Наряду с радиоактивным распадом ядерные реакции - основной источник сведений об атомных ядрах. Для записи ядерной реакции есть несколько способов. Два наиболее употребительных поясняются следующими примерами a + A b + B или A(a, b)B, p
+
Обычно более легкая частица называется - снарядом, более тяжелая -мишенью. При
столкновении протона с
Здесь 7Li* означает возбужденное состояние ядра 7Li. При упругом рассеянии налетающая частица и мишень не претерпевают каких-либо внутренних изменений и не появляется новых частиц. Первая ядерная реакция осуществлена в 1919 г. Резерфордом +
переверни |
14. Общие ограничения для сечения реакций Сечение
это область при попадании в которую
частица вызывает реакцию. В области
низких энергий длинна волны л сравни
сравнительно меньше радиуса действия
ядерных сил. Если энергия Е мала, то
Из этих формул следует, что не может быть неупругого канала без упругого, часть упругого канала всегда присутствует. Дифференциальное сечение уab реакции типа
может
быть представлена в виде
|
|
|
Если ядро - протяженный сферически симметричный и бесспиновый объект с плотностью заряда (r), то экспериментальное сечение упругого рассеяния электронов на нём будет отличаться от моттовского неким дополнительным множителем, который определяется только кулоновским взаимодействием и называется кулоновским форм-фактором
Величина форм-фактора F зависит от (r) и может быть рассчитана для любого (r), т.к. известен характер взаимодействия электронов с любым заряженным объектом - это электромагнитное взаимодействие. Электроны не участвуют в ядерном (сильном) взаимодействии и взаимодействуют с ядром почти исключительно посредством электромагнитного поля. Это важное преимущество электронов по сравнению с другими зондирующими частицами, такими, например, как , p, n, которые участвуют в ядерных взаимодействиях. Кроме того, на современном уровне знаний электрон можно считать точечной частицей.
|
|
где
Характерное
время
Нейтрон Обозначается “n”, открыт в 1932 году Дж. Чедвиком.
|
|
|
При отличии от нуля электрического заряда системы возникает его взаимодействие с внешним электрическим потенциалом. Под электрическим квадрупольным моментом Q ядра условились понимать величину
Величины электрического дипольного и квадрупольного моментов зависят от выбора системы координат. В дальнейшем мы будем использовать так называемую собственную (или внутреннюю) систему координат. Эта система жестко связана с ядром, перемещаясь и поворачиваясь вместе с ним. Начало собственной системы координат совпадает с центром распределения заряда и массы ядра. Можно легко показать, что электрический дипольный момент обращается в нуль при совпадении центра заряда с центром массы системы. Равенство нулю ядерного электрического дипольного момента как раз и говорит о таком совпадении.Если у ядра есть ось симметрии (как, например, у аксиально симметричного эллипсоида), то значение Q зависит от ориентации оси z собственной системы координат относительно этой оси симметрии. |Q| - максимален, если ось z совпадает с осью симметрии и как раз эту величину и рассматривают как собственный (внутренний) или классический квадрупольный момент ядра и обозначают Q0. Q0 характеризует отличие распределения заряда ядра от сферически симметричного (Q0=0 для сферически симметричного ядра), т.е. характеризует форму ядра (рис.3.2).
|
|
Входящие в формулу коэффициенты a1, a2, a3, a4 и a5 оцениваются из экспериментальных данных по знергиям связи ядер, что дает a1 = 15.75 МэВ; a2 = 17.8 МэВ; a3 = 0.71 МэВ; a4 = 94.8 МэВ; Формула Вайцзеккера позволяет по заданным значениям A и Z вычислять энергию связи ядра с погрешностью ~10 МэВ. При A 100 это дает относительную ошибку ~10-2. Наибольшее расхождение между эспериментально измеренными величинами энергии связи ядра и расчетами по формуле Вайцзеккера наблюдается в области магических чисел. Это объясняется тем, что в капельной модели не учитываются неоднородности распределения ядерной материи, обусловленные оболочечной |
|
Где ρ0 – плотность заряда в центре ядра, R – радиус половинной плотности, т.е. радиус на котором плотность равняется половине плотности в центре, a – указывает на то, насколько быстро идет спад.
|
|
Как правило в0
распад не происходит, наиболее вероятен
Существует гипотеза о микроскопических «черных дырах».
Фотон обладает четностью:
В процессе излучения ядро излучает фотоны с четностью:
|
Она
заключена в интервале от 18.61 кэВ ( Кулоновский барьер при -распаде можно не обсуждать. Он есть лишь для позитронов, образовавшихся внутри ядра. Главное то, что соотношение неопределенностей запрещает e долго оставаться внутри ядра (см. конец лекции).При -распаде возникает три продукта с произвольным распределением по энергии. При этом энергетический спектр каждого продукта непрерывен (рис.4.5). При e-захвате - два продукта и спектр дискретен. Непрерывность -спектров (e) натолкнула Паули в 1930 г. на идею о существовании неизвестной нейтральной частицы с полуцелым спином и очень малой массой. Ферми назвал её “нейтрино” (нейтрончик) после открытия в 1932 г. нейтрона. Нейтрино очень слабо взаимодействует с веществом и ускользает от наблюдателя. Её пробег в твердой среде 1015 км. Лишь в 1956 г. Райнесу и Коуэну удалось экспериментально подтвердить существование нейтрино и оценить сечение его взаимодействия с веществом ( 10-43 см2). |
Вероятность -распада равна произведению вероятности найти -частицу на границе ядра f на вероятность ee прохождения через потенциальный барьер D (прозрачность барьера) = ln2/T1/2 = f D. (5)
Вероятность прохождения -частицы через потенциальный барьер D описывается соотношением
где a- приведенная масса, Ea - энергия -частицы. В приближении Ea << Bk, где Bk - высота кулоновского барьера (предполагается, что барьер чисто кулоновский) описывается соотношениемDexp[-2{2azZe2/Eah2(/2-(Ea/Bk)}], (7) Вероятность нахождения -частицы на поверхности ядра можно грубо оценить через число соударений в единицу времени, которые испытывает -частица о внутренние границы барьера, тогда f=v/2Rv/2r0A1/3c/(2r0A1/3)[2(Ea+V0)/ac2]1/2(8) где v - скорость -частицы внутри ядра. Из (3), (7) и (8) можно получить приведенную выше зависимость от Ea (4).
|
|
В
микромире аналогом классического
момента
Если
выражать
Обобщая (3.27) на случай магнитного момента, возникающего за счет спина, запишем его в виде
где
gs
- безразмерная константа (спиновой
гиромагнитный множитель), учитывающий
отклонение собственного (спинового,
а значит квантового) магнитного момента
от классического (орбитального). В
значении
|
|
Пример:
|
Для
количественного описания вероятности
ядерной реакции используется эффективное
сечение - дифференциальное (d/d)
и полное ( Ядерные реакции рассматривают обычно либо в лабораторной системе координат (ЛСК), либо в системе центра инерции (СЦИ). ЛСК - система, в которой мишень покоится.
|
|
1 Ки = 3.7*1010 распадов/c,1 Бк = 1 распад/c. Распад исходного ядра 1 в ядро 2, с последующим его распадом в ядро 3, описывается системой дифференциальных уравнений dN1/dt = -
л
1N1
dN2/dt = -
л 2N2 +
л 1N1,
(6), где N1(t)
и N2(t)
-количество ядер, а л
1 и л
2 - постоянные
распада ядер 1 и 2 соответственно.
Решением системы (6) с начальными
условиями N1(0)
= N10;
N2(0)
=0 будет
Если
л 2
< л 1
( |
|

 (1.5)
(1.5)
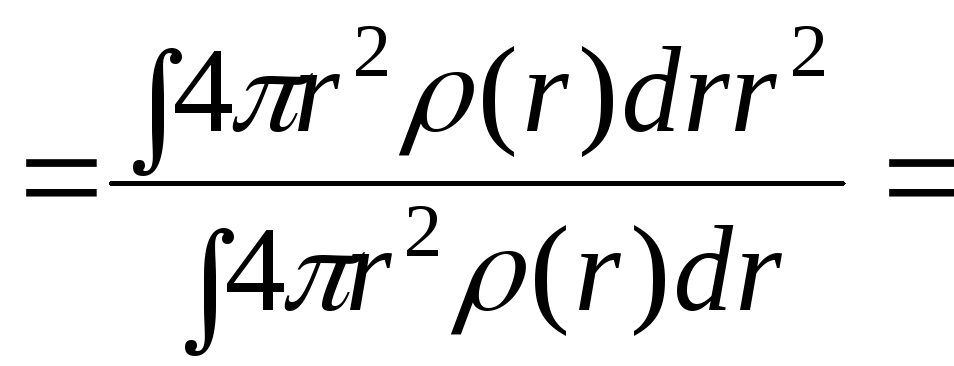


 |F|2.
1.6)
|F|2.
1.6)