Основные понятия численного решения уравнений

Собираясь использовать приближенные методы численного решения уравнений, мы не будем различать алгебраические (рациональные, иррациональные, линейные или нелинейные) и трансцендентные функции.

Итак, будем предполагать, что задано уравнение

f(x)=0 (1)

где функция f(x) – непрерывна на отрезке [a; b] и дифференцируема на интервале (a; b).

Требуется решить уравнение (1), т.е. найти множество всех его действительных корней с заданной точностью > 0.

Универсальные вычислительные алгоритмы основаны на том, что исходят из некоторого начального приближения x₀ одного из корней, которое затем улучшают (уточняют) до требуемой точности.

Как известно, приближенное нахождение корней нелинейного уравнения f(x)=0 обычно состоит из двух этапов:

а) отделение корней уравнения – отыскание достаточно малых отрезков, принадлежащих области определения f(x), в каждом из которых заключен один и только один корень уравнения (1).

б) уточнение приближенных корней – вычисление корней с заранее заданной точностью, если известно некоторое его начальное приближение в интервале, не содержащем других корней.

Согласно теореме Больцано-Коши [17], если непрерывная функция f(x) принимает на концах отрезка [a; b] значения разных знаков, то есть f(a)·f(b) <0, то внутри этого отрезка содержится, по крайней мере, один корень уравнения f(x) = 0, т.е. найдется хотя бы одно число x*(a; b) такое, что f(x*)=0.

Далее, если первая производная f'(x) не меняет знака на отрезке [a; b] (т.е. функция f (x) монотонна), то при выполнении условий теоремы Больцано-Коши уравнение f(x)=0 имеет на этом отрезке единственный корень.

Грубо отделить корни уравнения можно табулированием исследуемой функции. Однако наиболее изящным и эффективным следует признать графический метод при условии, что имеются удобные и надёжные средства построения графиков математических функций.

После отделения корней поведение графика функции на отрезке локализации корня может иметь один из следующих вариантов:

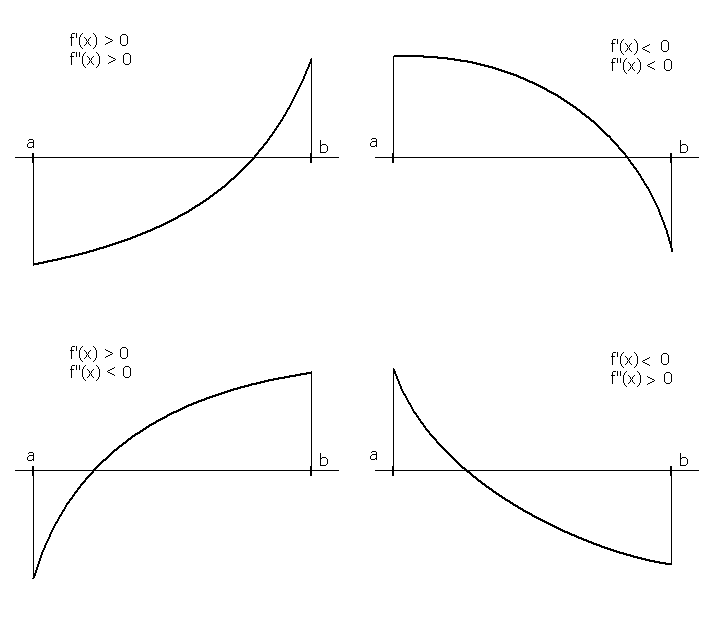
Поведение графика функции на отрезке локализации корня имеет существенное значение при программной реализации многих численных методов отыскания корней уравнений (метод Ньютона, метод секущих и др.) Некоторые численные методы уточнения корней уравнения (1) будут реализованы далее.

Задача 68. Метод дихотомии (метод половинного деления). Программа находит с погрешностью> 0 кореньx* уравнения F(x) = 0, где F(x) – непрерывная на отрезке [a, b] функция. Предполагается, что функция удовлетворяет условию F(a)*F(b) < 0, т.е на концах интервала [a, b] функция имеет значения разных знаков , что гарантирует наличие в заданном интервале по крайней мере одного корня уравнения.

Для нахождения корня отрезок [a; b] делится пополам точкой c = (a+b)/2 и далее выбирается тот полуинтервал, на концах которого знаки F(x) разные. Затем процесс деления повторяется до тех пор, пока длина интервала не станет меньше . В качестве x* можно взять, например, средину получившегося интервала. Описанный метод реализуется функцией zero().

// Программа отлажена вVisual Studio 2008

#include "stdafx.h"

#include <iostream>

#include <math.h>

#include <conio.h>

using namespace std;

double f(double x);

int main()

{

double zero(double ,double ,double );

float a,b,eps=1e-5;

a=1.2; b=1.5; setlocale(NULL, ".1251");

if(f(a)*f(b)>0)

{ cout<<"Не могу найти корень";

return 1;

}

cout<<"Корень равен "<<zero(a,b,eps);

getch();return 0;

}

double f(double x)

{

//return x*x-5*x+6;

return 2*x-cos(x);

}

double zero(double a,double b,double eps)

{

double c;

if(f(a)==0)

return a;

if(f(b)==0)

return b;

while (fabs(b-a)>eps)

{ c=(a+b)/2;

if (f(c)==0) return(c);

if (f(a)*f(c)<0)

b=c ;

else a=c;

}

return (a+b)/2;

}

Задача 69.Метод простых итераций. Программа находит корень x* уравнения F(x)=0 на заданном интервале [a, b] c заданной точностью > 0, где F(x) — непрерывная на [a, b] функция. Предполагается, что F(a)*F(b)<0, т.е. корень находится на отрезке [a, b].

Метод состоит в замене исходного уравнения эквивалентным ему уравнением x = (x). Это можно сделать всегда, притом не единственным способом (можно , например, прибавить x к левой и правой частям уравнения F(x)=0 ) .

Например, уравнение x³–9x+3=0 можно представить так:

1) 2)

3) x= x³ - 8x + 3 4)

Пусть известен отрезок изоляции корня [a; b], тогда за начальное приближение искомого корня можно принять, например,

В качестве каждого (k+1)-го приближения берут , к = 0, 1, 2...

Полученная последовательность сходится к искомому решению х* при возрастании k, если выполняется условие

|φ'(x)| ≤ M < 1

для всех х [a; b]. Если же |φ'(x)|>1, то итерационный процесс расходится.

Для конкретной оценки величины М (определяющей скорость сходимости: чем меньше М, тем быстрее сходимость) проще всего пользоваться формулой:

М = max |φ'(x)|,

где максимум берется по отрезку изоляции корня [a; b].

Оценив φ'(x) для четырех приведенных выше равносильных уравнений, соответствующих уравнению x³–9x+3=0 (учитывая, что корень уравнения заключен в интервале [0, 1]), придем к выводу, что только второе и четвертое уравнения годятся для применения к ним метода итераций; для остальных уравнений итерационный процесс будет расходящимся.

Процесс итераций обычно продолжают до тех пор, пока не будет выполнено условие

,

где - требуемая точность вычислений, аM= max |φ'(x)| , х [a; b]

Если вычисление производной φ'(x) и ее оценка затруднительны, то можно ограничить число итераций некоторым числом, например n ≤ 500.

Приведем здесь два решения поставленной задачи. Первый (упрощеный) вариант не использует оценку производной φ'(x). В контрольном примере (см. текст функции fi(x)) найден один из корней уравнения x – e^x + 2 = 0 на отрезке [-2, 0], а именно x1*   ‑1.841402, т. е. тот корень отрезка [a, b], где (x) = e^x < 1; второй корень этого уравнения x2*  1.146193.

// Программа отлажена в Borland С++ Builder 6 (8.04.2008)

// Вычисление корня F(x)=0 методом простых итераций

// упрощенный вариант

#include<stdio.h>

#include <iostream.h>

#include <conio.h>

#include<math.h>

// основная программа

voidmain()

{ inta,b; // наглость, конечно, но прототип согласует типы

// формальных и фактических параметров

floateps,x;

double iterac(double ,double ,double );

clrscr();

a=-2; b=0; eps=0.00001;

cout<<"корень = "<<iterac(a,b,eps)<<'\n';

getch();

}

double iterac(double a,double b,double eps)

// Эта процедура вычисляет корень уравнения

// методом простых итераций

{

double xn,xn1 ; int kit=0;

doublefi(doublex );

// выбор начального приближения

xn= (a+b)/2;

do

{

xn1= fi(xn);

if (fabs(xn1 - xn) < eps)

break;

xn = xn1;

kit++;

}

while(kit<500);

if(kit<500)

returnxn;

else

cout<<"Расходящийся процесс...";

}

// вычисление функции

double fi(double x )

{

//return sin(x) + 0.25;

returnexp(x)-2;

}

Ниже приведен более надёжный вариант программы, реализующей метод простых итераций – с оценкой модуля производной φ'(x).

// Программа отлажена вVisual Studio 2008

// iterac3.cpp Вычисление корня F(x)=0 методом

// простых итераций c оценкой максимума 1-й производной

// на [a, b]

#include "stdafx.h"

#include <stdio.h>

#include <iostream>

#include <conio.h>

#include <math.h>

// основная программа

int main()

{ double x, a, b ,M;

const double eps = 1.0e-4;

double iterac(double ,double ,double, double );

double dF1(double );

printf("Введи a b "); scanf("%lf %lf", &a, &b);

//оценка maксимума 1-й производной на [a, b]

x=a; M=fabs(dF1(x));

while(x< b)

{ x=x + eps*10;

if(fabs(dF1(x)) > M)

M=fabs(dF1(x));

}

printf("maximum = %lf\n", M);

if(M < 1)

printf("корень = %lf\n", iterac(a,b,eps,M));

else

printf("Расходящийся процесс...");

getch(); return 0;

}

double iterac(double a,double b,double eps, double M)

// Эта процедура вычисляет корень уравнения

// методом простых итераций

{

double xn,xn1 ; int kit=0;

double F(double x );

// {выбор начального приближения}

xn= (a+b)/2;

do

{

xn1 = F(xn);

if (fabs(xn1 - xn) < M*eps/(1 - M))

break;

xn= xn1;

kit++;

}

while(kit<500);

return xn;

}

// {вычисление функции}

double F(double x )

{

// return sin(x) + 0.25;

// return exp(x) - 2;

// return x*x*x - 8*x +3; //расходящийся процесс

return (x*x*x + 3) / 9; // на [0,1] x=0.337609

}

double dF1(double x )

{

return (x*x) / 3;

//return 3*x*x - 8; //

}

Задача 70.Составить программу и функции для вычисления с точностью ε=10^-5 значения корня уравнения F(x)=0 на интервале [a, b] методом Ньютона (касательных). Предполагается, что F(a)*F(b)<0, что гарантирует наличие в заданном интервале по крайней мере одного корня уравнения.

Пусть [a; b] – отрезок изоляции корня x* уравнения F(x)=0, F(a) · F(b) <0; функция F(x) непрерывна и дифференцируема на [a; b], производные F '(x) , F ''(x) сохраняют знак. Правило применения метода касательных следующее: в качестве начального приближения x₀ к корню x* выбирается тот конец отрезка изоляции (x₀ = a или x₀ = b), в котором выполняется условие F(x₀) · F ''(x₀)>0.

Уточнение корня осуществляется по следующей рекуррентной формуле

x_n+1 = x_n – , n = 0, 1, 2…,

Если на некотором шаге итерационного процесса окажется, что |x _n+1 – x _n| ≤ ε, то процесс завершается, и последнее полученное приближение x _n+1 принимают за приближенное значение корня с точностью ε.

Рассмотреть вариант:

x-Sinx-0.25=0

a=1, b=1.5

// Вычисление корня уравнения y=F(x) методом Ньютона (касательных)

#include <stdio.h>

#include <iostream.h>

#include <conio.h>

#include <math.h>

// основная программа

void main()

{

float eps,x,a,b ;

double newton(double, double, double);

clrscr();

a=1; b=2; eps=0.00001;

cout<<"корень = "<<newton(a,b,eps)<<'\n';

getch();

}

double newton(double a,double b,double eps)

// Эта процедура вычисляет корень уравнения

// методом Ньютона (касательных)

{

double xn,xn1 ;

double F(double x );double dF1(double x );double dF2(double x );

// {выбор начального приближения}

if(F(a)*dF2(a) > 0)

xn= a;

else

xn= b;

do

{

xn1= xn - F(xn) / dF1(xn);

if (fabs(xn1 - xn) < eps)

break;

xn= xn1;

}

while(1);

return xn;

}

// {вычисление функции}

double F(double x )

{

returnx - sin(x) - 0.25;

}

// {вычисление второй производной}

double dF2(double x )

{

return sin(x);

}

// {вычисление первой производной}

doubledF1(doublex )

{

return1 - cos(x);

}

Задача 71.Ниже представлен программный проект, состоящий из нескольких самостоятельных модулей:

1. Вывод треугольника

2. Падающая звезда

3. Рисуем фигуры

Для выбора любого из них используется профессиональное меню, с подсветкой выбираемого пункта меню и перемещением подсветки с помощью клавиш управления. Не поленитесь и разберитесь, как устроено это меню. Пригодится.

// Программа отлажена в Borland С++ Builder 6 (31.03.2008)

#include <stdio.h>

#include <conio.h>

#include <stdlib.h>

#include <dos.h>

#include <iostream.h>

// upr_mord.cpp перемещение символа по экрану

// рисование фигур, используя клавиши управления

voidupr_mor4()

{

int x,y;

int i,j,maxx=79,maxy=24;

unsigned char c='\002', ch; // int ch;

i=maxx/2;j=maxy/2; x=0;y=0;

clrscr();gotoxy(i,j); putch(c);

while( (ch=getch()) !=27)

{

if(ch==0) //&& kbhit())

ch=getch();

switch(ch)

{

case 72: x=0;y=-1; break;

case 75: x=-1; y=0; break;

case 77: x=1; y=0; break;

case 80: x=0; y=1; break;

case 71: x=-1; y=-1; break;

case 73: x=1; y=-1; break;

case 79: x=-1; y=1; break;

case 81: x=1; y=1; break;

}

i=i+x; j=j+y;

if(i<1) {i=1; j++;}

if(i>maxx-1) {i=maxx-1;j++;}

if(j<1) {j=1;i++;}

if(j>maxy-1) {j=maxy-1;i++;}

gotoxy(i,j); putch(c);

Sleep(100); //задержка выполнения программы

}

getch();

}

/*ПАДАЮЩАЯ ЗВЕЗДА*/

voidpadenie()

{

intk;charc;

clrscr();

printf(" ВВЕДИ ПАДАЮЩИЙ СИМВОЛ\n");

c=getchar();

for(k=1;k<=23;k++)

{

clrscr();

gotoxy(40,k);

putch(c);

// Задержка выполнения программы

for(longi=0;i<99887655;i++);

}

getch();

}

// печать символа заданное число раз

void put_ch(int m,char ch)

{

while(m>0)

{

putchar(ch);

m--;

}

}

// Вывод треугольника на экран

voidmmm()

{

clrscr();

int y,i=0;char x;

cout<<" ВВЕДИ СИМВОЛ - ЗАПОЛНИТЕЛЬ ";cin>>x;

cout<<" ВВЕДИ ВЫСОТУ ТРЕУГОЛЬНИКА ";cin>>y;

while(i<y)

{

put_ch(39-i,' '); // печать 39-i пробелов

put_ch(2*i+1,x); // печать 2*i+1 символов

i++;

cout<<'\n';

}

getch();

}

//ОСНОВНАЯ ПРОГРАММА

#define cfone textbackground(BLUE)

const int m= 4,L=80;

colorputs(int cfon,int cl,int y) ;

charstr[m][L]={" Вывод треугольника ",

" Падающая звезда ",

" Рисуем фигуры ",

" Окончание работы " } ;

void main ()

{

int y=0,j;

m5:cfone;textcolor(YELLOW);

clrscr();

gotoxy(19,24);

textcolor(LIGHTRED);

cprintf("\030 Выбери пункт меню и жми Enter \031");

for (j=0;j<4;j++)

colorputs(LIGHTGRAY,YELLOW,j);

m6:

colorputs(LIGHTRED,YELLOW,y);

m7:

switch(getch())

{

case 0 :switch(getch())

{

case 72 :colorputs(LIGHTGRAY,YELLOW,y);

y--;

if (y<0) y=3;

goto m6;

case 80 :colorputs(LIGHTGRAY,YELLOW,y);

y++;

if (y>3) y=0;

goto m6;

}

goto m7;

case 13 :switch(y)

{

case 0 : textcolor(LIGHTRED);cfone;

//gotoxy(59,6); cprintf("* ждите *");

mmm(); // Вызов функции построения треугольника

gotom5;

case 1 : textcolor(LIGHTRED);cfone;

gotoxy(59,3); cprintf("* ждите *");

padenie(); // Вызов функции *ПАДАЮЩАЯ ЗВЕЗДА*

goto m5;

case 2 : textcolor(LIGHTRED);cfone;

gotoxy(49,13);

cprintf("* жмиEnterдля завершения *");

upr_mor4(); // Вызов функции перемещения символа

goto m5;

case 3 :cfone;clrscr();exit(0);

}

}

goto m7;

}

colorputs(int cfon,int cl,int y)

{

textcolor(cl);textbackground(cfon);

gotoxy(25,2+y*2);

cprintf("%s",str[y]);

}

Задача 72. Создать программу, которая позволяет найти те числа из заданного диапазона [A, B] целых чисел, в двоичном представлении которых максимальное количество двоичных единиц. Напечатать как двоичное, так и десятичное представление таких чисел (их может быть несколько).

// Программа отлажена вVisual Studio 2008

#include "stdafx.h"

#include <stdio.h>

#include <iostream>

#include <math.h>

using namespace std;

// Функция подситывает число двоичных единиц в числе

short int count (int a)

{ unsigned int maska=1<<8*sizeof(int)-1;

short int k=0;

while(maska)

{

if(a & maska)

k++;

maska >>= 1;

}

return k;

}

// функция выводит на экран двоичное представление числа

void put_bite(int a)

{

unsigned int maska=1<<8*sizeof(int)-1;

while(maska)

{

if(a&maska)

putchar ('1');

else

putchar('0');

maska=maska>>1;

}

}

//

int main()

{

int A,B,a,max=0,k;

// Устанавливаем локализацию для выходного потока

wcout.imbue( locale( "rus_rus.866" ) );

// Выводим строку на русском языке !

wcout<<L"Ввди начало диапазона "; cin>>A;

wcout<<L"Ввди конец диапазона "; cin>>B;

for (a=A; a<=B; a++)

{

k=count(a);

if (k > max)

max = k;

}

wcout<<L"максимальное число двоичных единиц = "<<max<<"\n";

for(a=A;a<=B;a++)

{

k=count(a);

if(k==max)

{

cout<<a<<" = ";

put_bite(a);

cout<<"\n";

}

}

return 0;

}

Протокол работы программы:

Ввди начало диапазона 16383

Ввди конец диапазона 32678

максимальное число двоичных единиц = 14

16383 = 0000000000000000 0011111111111111

24575 = 0000000000000000 0101111111111111

28671 = 0000000000000000 0110111111111111

30719 = 0000000000000000 0111011111111111

31743 = 0000000000000000 0111101111111111

32255 = 0000000000000000 0111110111111111

32511 = 0000000000000000 0111111011111111

32639 = 0000000000000000 0111111101111111

Для продолжения нажмите любую клавишу...

Задача 73. Создать программу, позволяющую вывести на экран треугольник Паскаля, который имеет следующий вид:

1

1 1

1 2 1

1 3 3 1

1 4 6 4 1

1 5 10 10 5 1

1 6 15 20 15 6 1

1 7 21 35 35 21 7 1

1 8 28 56 70 56 28 8 1

1 9 36 84 126 126 84 36 9 1

Этот треугольник можно построить, формируя двумерный массив, в котором каждая последующая строка вычисляется на основе предыдущей по такому правилу: каждый её элемент (не считая крайних, которые всегда равны 1) равен сумме двух стоящих над ним соседних элементов предыдущей строки.

Мы здесь реализуем алгоритм, основанный на том, что каждая строка треугольника представляет последовательность биномиальных коэффициентов разложения в ряд бинома Ньютона:

(j=0,1,2, …, n)

где a, b – действительные числа, n – целое,

, ( j=0,1,2,...,n)

Для вычисления биномиальных коэффициентов многократно используется функция нахождения факториала натурального числа fact(). Для позиционирования курсора в заданную точку строки экрана при выводе символа использована уже известная функция put_ch().

// Программа отлажена вVisual Studio 2008

//Треугольник Паскаля

#include "stdafx.h"

#include<stdio.h>

#include<conio.h>

void put_ch(char c,int n)

{

while(n)

{

putchar(c);

n--;

}

}

long fact(int n)

{ long f=1;

for(int k=2; k<=n; k++)

f*=k;

return f;

}

int main()

{long k1, k2, k3, cjn;

int n=10;

for(int i=0; i<=n; i++)

{

k1=fact(i);

put_ch(' ',39-2*i);

for(int j=0; j<=i; j++)

{

k2=fact(j);

k3=fact(i-j);

cjn= k1/k2/k3;

printf("%-5ld",cjn);

}

printf("\n");

}

getch();return 0;

}

Задача 74. Выдать на экран в виде таблицы значения функции F(x), заданной с помощью ряда Тейлора, вычисленные приближенно с заданной точностью = 0.001 на интервале [a, b] с шагом . Каждая строка таблицы должна содержать значение аргумента x, значение функции F(x) и значение этой же функции, полученной с помощью соответствующей библиотечной функции . Для вычисления значения F(x) оформить функцию. Остальные действия предусмотреть в вызывающей программе.

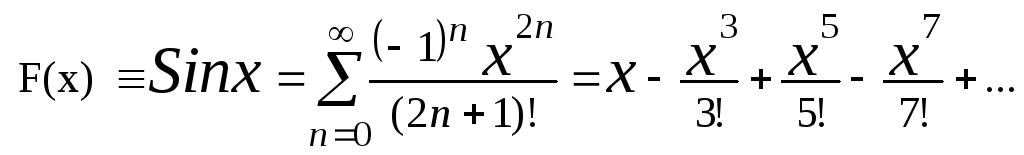|x|<

// Программа отлажена вVisual Studio 2008

#include "stdafx.h"

#include<conio.h>

#include<stdio.h>

#include<math.h>

#include <iostream>

using namespace std;

double sinus(double , double ); //прототип функции

int main()

{ double a, b, x, eps=0.001, dx = 0.1;

// Устанавливаем локализацию для выходного потока

wcout.imbue( locale( "rus_rus.866" ) );

// Выводим строку на русском !

wcout<< L" Введи А " ; scanf("%lf", &a);

wcout<< L" Введи B " ; scanf("%lf", &b);

wcout<< L" Аргумент По итерационной формуле По стандартной \

функции\n";

x=a;

while (x < b)

{

printf("%8.2lf %20.6lf %20.6lf\n", x, sinus(x,eps), sin(x));

x = x + dx;

}

_getch(); return 0;

}

double sinus(double x, double eps)

{

double u = x, S = u, v = -x*x; int n = 0;

while(fabs(u)>eps)

{

u = (u*v)/((2*n+2)*(2*n+3));

S=S+u; n++;

}

return S;

}

Задача 75. Программный проект предназначен для вычисления корня уравнения методом дихотомии и включает три модуля, расположенные в трех разных файлах. Объединение достигается применением препроцессорной команды #include “имя_файла”.

// Программа отлажена вVisual Studio 2008

#include "stdafx.h"

#include <iostream>

#include <math.h>

#include <conio.h>

using namespace std;

//Создать папку ZERO1 и разместиь там файлы non.cpp и nonn.cpp

#include "d:\MY_VS2008\ZERO1\non.cpp"

double f(double x); //прототип функции

void main()

{

double zero(double ,double ,double );

float a,b,eps;

a=0;b=1.5; eps=1e-5;

cout<<"Корень равен "<<zero(a,b,eps);

getch();

}

/*

//Этот фрагмент есть файл non.cpp

#include "d:\MY_VS2005\ZERO1\nonn.cpp"

//функция находит корень уравнения методом дихотомии

double zero(double a,double b,double eps)

{

double c;

while (fabs(b-a)>eps)

{ c=(a+b)/2;

if (f(c)==0) return(c);

if (f(a)*f(c)<0) b=c ;

else a=c;

}

return (a+b)/2;

}

//Этот фрагмент есть файл nonn.cpp

double f(double x)

{

//return x*x-5*x+6;

return 2*x - cos(x);

}

*/

Задачи для самостоятельного решения

1. Составить функцию для изображения на экране каждой из приведенных ниже фигур:

1)  2)  3) 

  

  

  

  

  

  

  

4.  5) @@@@@@@@@@@ 6) @@@@@@@@@@@

 @@@@@@@@@ @ @

 @@@@@@@ @ @

 @@@@@ @ @

 @@@ @ @

 @ @





2.Составить функцию, которая выводит на экран «вертушку», используя символы,,,.

3. Назовём натуральное число палиндромом («перевёртышем»), если его запись читается одинаково с начала и с конца (например: 4774, 35, 22, 7) . Составить функцию, которая позволяет найти в заданном интервале [ 1, N ] все числа – палиндромы.

4. Составить функцию, которая позволяет найти в заданном интервале [ 100, N ] все целые числа, которые делятся на каждую свою цифру ( кроме 0 ) без остатка.

5. Составить функцию, которая позволяет найти в заданном диапазоне [ 1,М ] все целые числа, которые делятся на сумму своих цифр.

6. Создать функцию, которая позволяет найти и выдать на экран все натуральные трехзначные числа, в которых сумма цифр кратна трём.

7. Создать функцию, которая позволяет найти и выдать на экран все натуральные трехзначные числа, в которых сумма крайних цифр равна средней .

8. У гусей и кроликов вместе 32 лапы. Составить функцию, которая позволяет определить, сколько было тех и других.

9. Составить функцию, которая позволяет найти все натуральные четырехзначные числа, в записи которых нет двух одинаковых цифр.

10. Составить функцию, которая позволяет найти для заданного натурального числа N его сумму с числом М, полученным из N перестановкой цифр в обратном порядке.

11. Составить функцию, которая проверяет, являются ли два заданные числа «перевёртышами» друг друга . Например:

127 и 721 — да

127 и 172 — нет

12. Натуральное число из k цифр является числом Армстронга, если сумма его цифр, возведён­ных в k-ю степень, равна самому числу

(например, 153 = 1³ + 5³ + 3³ ).

Составить функцию, которая позволяет получить все числа Армстронга, состоящие из k цифр.

13. Создать функцию, которая позволяет сформировать и выдать на экран последовательность из N чисел Фибоначчи. Эти числа определяются так: f₀ = 1, f₁ = 1, а каждое следующее число равно сумме двух предыдущих:

f_n+1 = f_n + f_n-1 n = 1, 2, 3, …

Вот несколько первых чисел Фибоначчи: 1, 1, 2, 3, 5, 8, 13, 21, …

N передать функции как параметр.