4. Построение гистограммы частоты признака

Прежде чем воспользоваться процедурой Excel построения гистограммы необходимо найти границы интервалов группировки

Вычислим интервалы группировки.

В рассматриваемом варианте n = 53.

Число интервалов группировки k в Excel вычисляется по формуле

,

где, скобки означают – округление до целой части числа в меньшую сторону, следовательно.= 8.

Величина интервала группировки вычисляется по формуле

Тогда, так как , то

.

Строгого научного обоснования для определения числа интервалов группировки и их величинынет. Существует много эмпирических формул для определения числаk.

Разброс значений числа k (числа интервалов группировки), который дают эти формулы, позволяет исследователю выбрать удобные для вычисления границы частичных интервалов группировки. Так в рассматриваемом варианте исходных данных 99,5, а максимальное значение117,88. Дробные величины неудобны для восприятия.

Тогда, пусть левая (нижняя) граница всего интервала будет равной = 98 (меньше99,5), а величина интервала группировки,

следовательно, = 98+3 = 101,

= 101+3 = 104,

=107,

= 110

= 113

= 116

= 119

Пусть верхняя граница последнего частичных интервалов группировки будет = 119, так как117,88 входит в этот последний интервал.

Получили границы интервалов группировки (карманы, как их называют вExcel) красивыми целыми числами. Занесите полученные результаты в столбецExcel,рис.7.

Рис. 7. Массив границ (карманов) группировкиA57:A64

Теперь можно приступить к построению гистограммы.

В главном меню Excel выбрать Данные → Анализ данных → Гистограмма → ОК.

Далее необходимо заполнить поля ввода в диалоговом окне Гистограмма.

Входной интервал: 53 случайных чисел (вариант, значений признака) в ячейках $B$2: $B$54;

Интервал карманов: ввести массив границ интервалов группировки (карманов) ис 2 A57:A64;

Выходной интервал: адрес ячейки, с которой начинается вывод результатов процедуры Гистограмма;

Вывод графика – поставьте галочку. OK.

Рис. 8. Диалоговое окно Гистограмма с заполненными полями.

Если в диалоговом окне Гистограмма поле ввода Интервал карманов не заполняется, то процедура вычисляет число интервалов группировки k и границы интервалов автоматически.

В результате выполнения процедуры Гистограмма появляется таблица, содержащая границы интервалов группировки (столбец –Карман) и частоту попадания признака выборки в k–ый интервал (столбец – Частота).

Справа от таблицы – график гистограммы.

Рис. 9. Фрагмент листа Excel с результатами процедуры Гистограмма

Принято столбики гистограммы строить без зазора.

Приведите гистограмму к виду как показано на рис. 10.

Для этого щелкните правой кнопкой мыши на столбике диаграммы и выберите Формат ряда данных → Без зазора → Нет заливки. Выберите цвет границ, стили границ и толщину линии границ.

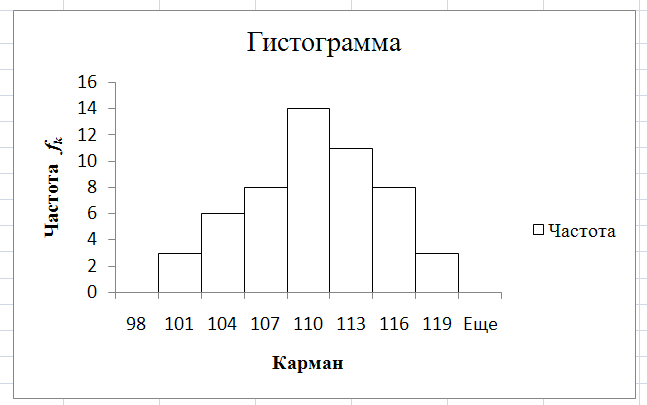
Рис. 10. Гистограмма частот

При вычислении моды для интервального вариационного ряда необходимо определить модальный интервал (по максимальной частоте), а затем – значение моды по формуле

Модальный интервал

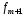
Рис 11. График гистограммы с модальным интервалом, интервалом предшествующим модальному и следующим за модальным интервалам.

Для рассматриваемого варианта:

= 107, = 110 - это границы модального интервала

= 8– частота интервала, предшествующего модальному интервалу;

= 14– частота модального интервала;

= 11 – частота интервала, следующего за модальным интервалом.

Среднее = 108,9134, Мода =109 , Медиана = 109,5;

Медиану можно найти графическим способом, построив кумуляту.

Для построения кумуляты в таблице Карман-Частота добавьте столбец накопленных эмпирических частот . ()

Рис 12. Таблица Карман-Частота, полученная при построении гистограммы, с добавленным столбцом накопленных эмпирических частот.

Далее постройте график кумуляты.

Медиана соответствует варианте, стоящей в середине ранжированного ряда. Положение медианы определяется ее номером .

На оси графика кумуляты отложите. Найдите соответствующее значение варианты

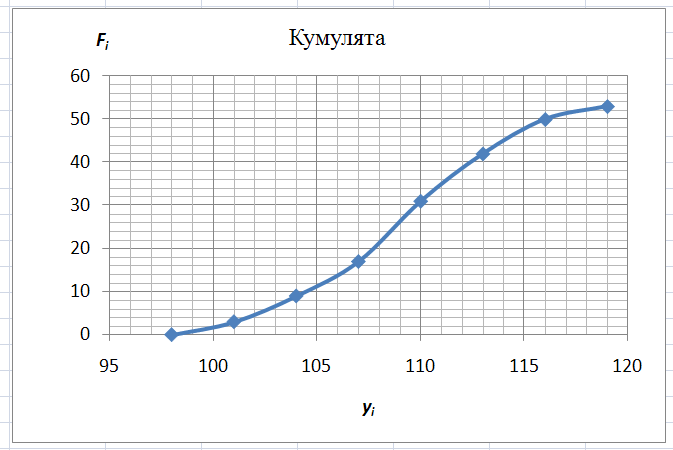
Рис 13. График кумуляты с определенным графическим способом значением .

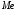Приблизительное равенство оценок = 108,9134, = 109 и = 109,5 позволяет предположить, что распределения признаков генеральной совокупности имеет нормальный закон.

По виду гистограммы можно принять гипотезу о нормальном распределении признаков (случайных чисел) выборки.

Далее, для того чтобы убедиться в правильности выбранной гипотезы (по крайней мере визуально) надо, первое – построить график гипотетического нормального закона распределения, выбрав в качестве параметров (среднее и среднее квадратическое отклонение) их оценки (оценки среднего и стандартного отклонения), и совместить график гипотетического распределения с графиком гистограммы.

И, второе – используя критерий согласия Пирсона установить справедливость выбранной гипотезы.