2. Экспоненциальный (показательный) закон распределения
Непрерывная случайная величина X называется распределенной по показательному закону, если ее плотность распределения вероятности задается формулой:
где λ - некоторое положительное число.
Функция распределения имеет вид:
По показательному закону распределены – время безотказной работы элементов различных приборов, время обслуживания заявок в системе массового обслуживания, случайные отрезки времени между последовательными наступлениями редких событий.
λ - интенсивность потока событий (число событий в единицу времени).
Задание 2. Непрерывная случайная величина X распределена по показательному закону с параметром λ = 0,5. Постройте функцию и плотность распределения вероятностей случайной величины. Вычислите вероятность попадания X в интервал (2, 5).
1. Построение таблицы плотности и функции распределения показательного закона.
Таблица показана на рис. 11.
В ячейке A2 находится значение параметра λ = 0,5.
В столбце B2:B12 размещены значения переменной X.
В ячейку C2 занесена формула ЭКСПРАСП(B2; $A$2; 0).
Как обратиться к библиотеке функций Excel, занести формулу ЭКСПРАСП в ячейку и заполнить поля ввода – известно.
Функция
ЭКСПРАСП вычисляет значения функции
распределения
или функция плотности f(x)
экспоненциального
(показательного) распределения,
соответствующие заданному значению
аргумента
x.
Функция ЭКСПРАСП имеет следующий синтаксис:
ЭКСПРАСП(x; лямбда; интегральная)
x
–
заданное значение аргумента, для которой
вычисляется функция распределения
или функция плотности f(x);
лямбда – параметр показательного распределения λ;
интегральная – логическая переменная, принимающая значения 0 или 1:
- если логической переменной интегральная задать значение 0 , то функция ЭКСПРАСП вычислят плотность показательного распределения f(x);
- если логической переменной задать значение 1, то вычисляется функция распределения F(x).
Формула ЭКСПРАСП(B2; $A$2; 0), занесенная в ячейку C2, размножена на ячейки всего столбца C2:C12.
В ячейку D2, для получения значения функции распределения F(x), занесена формула ЭКСПРАСП(B2; $A$2; 1)
Далее формула ЭКСПРАСП(B2; $A$2; 1), находящаяся в ячейке D2, размножена на весь столбец D2:D12.
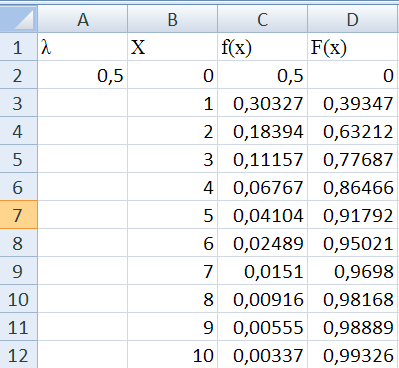
Рис. 11. Таблица значений плотности показательного распределения f(x) и функции распределения F(x) для заданного значения параметра λ = 0,5
2. Построение графика плотности распределения и графика функции распределения вероятностей не должно вызвать затруднений.
Рис. 12. Графики функции плотности показательного распределения f(x) и функции распределения F(x)
3. Вычисление вероятности попадания случайной величины в интервал (2, 5).
Составьте программу вычислений как показано на рис. 13.
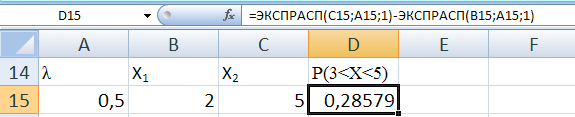
Рис. 13. Вычислите вероятность попадания случайная величина в интервал (2, 5),
λ = 0,5 – параметр показательного распределения
x1 = 2, x2 = 5.
ЭКСПРАСП(C15;
A15;
1)- ЭКСПРАСП(B15;
A15;
1) = 0,28579
Проверьте вычисления в Excel? Используя аналитические вычисления:
Отчет в Excel должен содержать таблицы, показанные в приложении 1.
Приложение 1
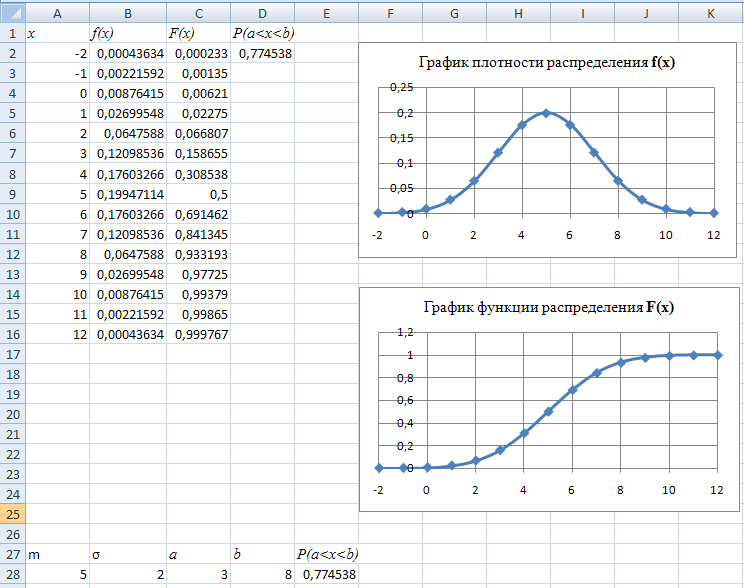
Приложение 2.
Отчет
Лабораторная работа №4. Законы распределения непрерывных случайных величин.
Группа 190-2. Мельников Иван Л. Вариант №5.
Отчет должен содержать тексты заданий, исходные данные и распечатки вычислений в Excel как показано в приложении 1.
Дата сдачи работы:
Проверил:
Приложение 3
Варианты лабораторной работы №4
Задание 1. Непрерывная случайная величина X распределена по нормальному закону с параметрами m, σ. Построить функцию распределения и плотность распределения вероятностей. Вычислить вероятность попадания случайная величина в интервал (a, b).
|
Задание 1 |
|||
|
Вариант |
m |
σ |
(a, b) |
|
1, 12, 23 |
6 |
2 |
(3,5; 8,3) |
|
2, 13, 24 |
4 |
1,5 |
(2,7; 6) |
|
3, 14, 25 |
7 |
1,9 |
(3,4; 7,5) |
|
4, 15, 26 |
3 |
0,8 |
(3,4; 7,5) |
|
5, 16, 27 |
5 |
1,2 |
(3,5; 7) |
|
6, 17, 28 |
8 |
2,1 |
(5,1; 10,5) |
|
7, 18, 29 |
10 |
2,9 |
(1,4; 8,5) |
|
8, 19, 30 |
9 |
2,5 |
(3,1; 7,5) |
|
9, 20, 31 |
11 |
2,4 |
(7,4; 15,5) |
|
10, 21, 32 |
5 |
2,1 |
(5,5; 8,5) |
|
11, 22, 33 |
7,5 |
2,9 |
(4,4; 8,5) |
Задание 2. Непрерывная случайная величина X распределена по показательному закону с параметрами λ. Построить функцию распределения и плотность распределения вероятностей случайная величина. Вычислить вероятность попадания случайная величина X в интервал (a, b).
|
Задание 2 |
||
|
Вариант |
λ |
(a, b) |
|
1, 12, 23 |
0,5 |
(3, 15) |
|
2, 13, 24 |
0,6 |
(1,5; 5) |
|
3, 14, 25 |
0,4 |
(2,5, 14) |
|
4, 15, 26 |
0,35 |
(1,7; 8) |
|
5, 16, 27 |
0,85 |
(3,1; 12) |
|
6, 17, 28 |
0,7 |
(0,8; 10) |
|
7, 18, 29 |
0,65 |
(0,5; 9) |
|
8, 19, 30 |
0,57 |
(1,5; 8) |
|
9, 20, 31 |
0,48 |
(3; 9,5) |
|
10, 21, 32 |
0,74 |
(1,2; 10) |
|
11, 22, 33 |
0,57 |
(2,8; 15) |