
ЛР-5 РЕГРЕССИЯ
.docx
Лабораторная работа №5. Регрессионный анализ.
Лабораторная работа выполняется в Excel 2007.
Цель работы – построение корреляционного поля, отыскание коэффициентов линейной регрессии и построение линии среднеквадратической регрессии средствами Excel.
Задана таблица значений контролируемой величины X и случайной величины Y. Построить корреляционное поле. Найти параметры линейной среднеквадратичной регрессии. Построить линию линейной регрессии.
|
xi |
1 |
2 |
3 |
4 |
5 |
|
yi |
18 |
13 |
11 |
14 |
10 |
1. Составьте таблицу значений контролируемой величины X и случайной величины Y, как показано на рис. 1 и в прилагаемом отчете.

Рис. 1. Таблица исходных данных и параметров уравнения регрессии.
К методическому руководству прилагается отчет по лабораторной работе в Excel/
2. Используя исходные данные, постройте корреляционное поле (так это называется).
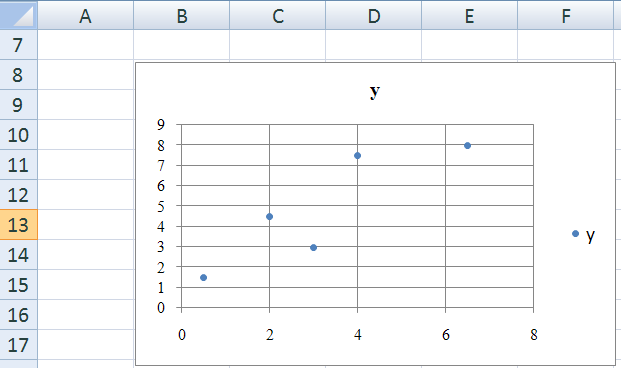
Рис. 2. График корреляционного поля.
3. Уравнение линейной регрессии имеет вид:
 -
уравнение линейной регрессии;
-
уравнение линейной регрессии;
 -
уравнение линейной регрессии, приведенное
к виду уравнения с угловым коэффициентом;
-
уравнение линейной регрессии, приведенное
к виду уравнения с угловым коэффициентом;
 -
выборочный коэффициент регрессии;
-
выборочный коэффициент регрессии;
 -
выборочная постоянная регрессии;
-
выборочная постоянная регрессии;
 -
среднее квадратическое отклонение X;
-
среднее квадратическое отклонение X;
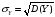 -
среднее квадратическое отклонение Y.
-
среднее квадратическое отклонение Y.
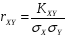 -
коэффициент корреляции;
-
коэффициент корреляции;

 -
корреляционный момент;
-
корреляционный момент;
 ;
;
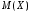 -
математическое ожидание случайной
величины X;
-
математическое ожидание случайной
величины X;
 -
математическое ожидание случайной
величины Y.
-
математическое ожидание случайной
величины Y.
4.
Составьте таблицу параметров уравнения
регрессии
 ,
,
 ,
,
 ,
,
 ,
,
 (как показано на рис.1):
(как показано на рис.1):
-
для вычисления математического ожидания
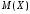 и
и
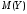 используйте функцию СРЗНАЧ
из категории Статистические
(и не спрашивайте, как это сделать);
используйте функцию СРЗНАЧ
из категории Статистические
(и не спрашивайте, как это сделать);
-
для вычисления среднего квадратического
отклонения
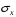 и
и
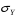 используйте функцию СТАНДОТКЛОН
из категории Статистические
(как это сделать, можете спросить у
преподавателя, если не боитесь);
используйте функцию СТАНДОТКЛОН
из категории Статистические
(как это сделать, можете спросить у
преподавателя, если не боитесь);
-
для вычисления коэффициента корреляции
 используйте функцию КОРРЕЛ из
категории Статистические.
используйте функцию КОРРЕЛ из
категории Статистические.
4.
В ячейку C2
внесите формулу
 ,
используя результаты вычислений
параметров
,
используя результаты вычислений
параметров
 ,
,
 ,
,
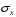 ,
,
 и
и
 ,
как показано в строке ввода формул на
рис. 1.
,
как показано в строке ввода формул на
рис. 1.
Размножьте
эту формулу в столбце ячеек C2:C6
с меткой
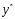 .
.
5. На графике корреляционного поля добавьте линию регрессии.
Excel располагает еще одним способом отыскания сглаживающей линейной зависимости и построении линии регрессии.
6.
Скопируйте исходные данные в ячейку
A20.
Найдите параметры уравнения линейной
регрессии
 следующим образом:
следующим образом:
-
 - выборочный коэффициент регрессии
отыскивается помощью функцию НАКЛОН
из категории Статистические;
- выборочный коэффициент регрессии
отыскивается помощью функцию НАКЛОН
из категории Статистические;
-
 - выборочная постоянная регрессии
отыскивается помощью функцию ОТРЕЗОК
из категории Статистические;
- выборочная постоянная регрессии
отыскивается помощью функцию ОТРЕЗОК
из категории Статистические;
Результаты вычислений показаны на следующем рисунке:
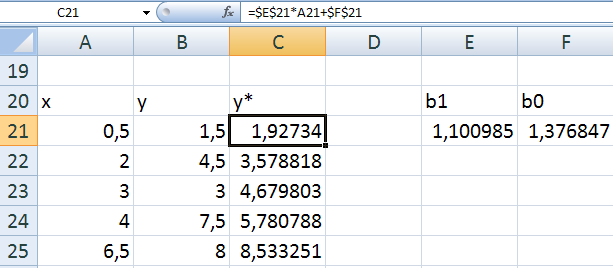
Рис.
3. Таблица вычисления параметров
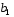 ,
,
 и данных y*
для
построения линии регрессии
и данных y*
для
построения линии регрессии
7. Постройте совмещенный график корреляционного поля и линии регрессии.
Еще одна функция Excel для отыскания линейной регрессии и построении линия линии тренда.
8. Выберите в Главном меню последовательно следующие закладки Данные →Анализ данных →Регрессия.
Заполните свободные поля в диалоговом окне Регрессия соответствующими данными как показано на рис 4:
Входной интервал y: исходные данные y;
Входной интервал x: исходные данные x;
Выходной интервал: A47
Поставьте галочку в окне график подбора. ОК!!!
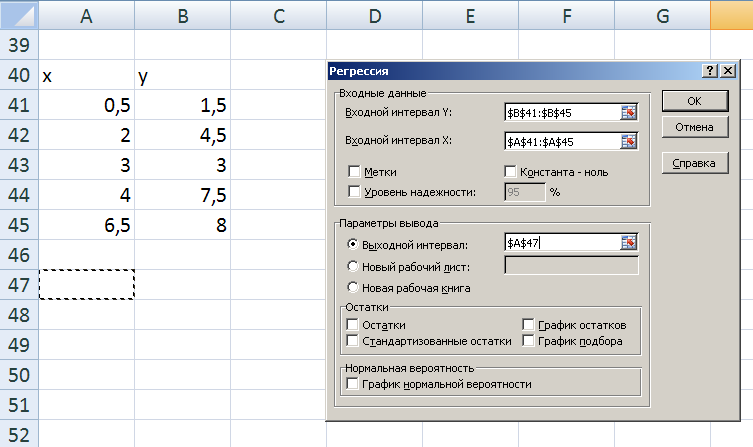
Рис. 4. Диалоговое окно Регрессия
Процедура Регрессия выводит график исходных данных и сглаживающую линию регрессии (график надо отформатировать).
В
третьей
таблице ВЫВОД
ИТОГОВ
находятся интересующие нас параметры
регрессии
 и
и
 - коэффициенты Y-пересечение
и переменная X
. Кроме того процедура Регрессия
выводит на экран большое количество
других результатов в виде таблиц, которые
нам потребуются в дальнейшем, при решении
задач эконометрики.
- коэффициенты Y-пересечение
и переменная X
. Кроме того процедура Регрессия
выводит на экран большое количество
других результатов в виде таблиц, которые
нам потребуются в дальнейшем, при решении
задач эконометрики.
Есть в Excel еще два способа построения линии тренда.
Скопируйте исходные данные X и Y в блок, начиная с ячейки A28, и постройте еще раз график корреляционного поля (Вставка→График→Точечный)
Щелкнув правой кнопкой мыши на маркере одной из точек графика корреляционного поля, активизируйте, таким образом, диалоговое окно форматирования данных ряда. Выберите опцию Добавить линию тренда … (как показано на рис. 5)
В открывшемся окне Формат линии тренда установите Параметры линии тренда:
- Линейная
- показать уравнение на диаграмме
- поместить на диаграмму величину достоверности аппроксимации.
При
установке флажка в поле
- поместить на диаграмму величину
достоверности аппроксимации,
на диаграмму выводится значение
коэффициента детерминации
 .
.
Чем
лучше выбрана функция регрессии и чем
меньше различие между наблюденными
значениями
 и
расчетными
и
расчетными
 ,
тем
ближе
,
тем
ближе
 к единице.
к единице.

Рис. 5. Диалоговое окно Регрессия
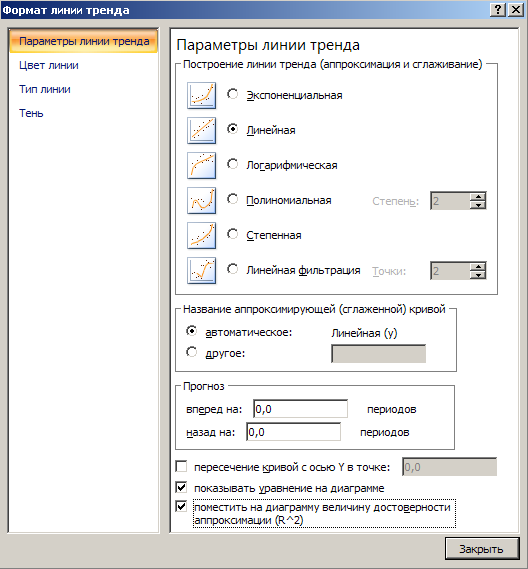
Рис. 6. Диалоговое окно Регрессия
После выполнении процедуры Добавить линию тренда… график корреляционного поля приобретет вид:
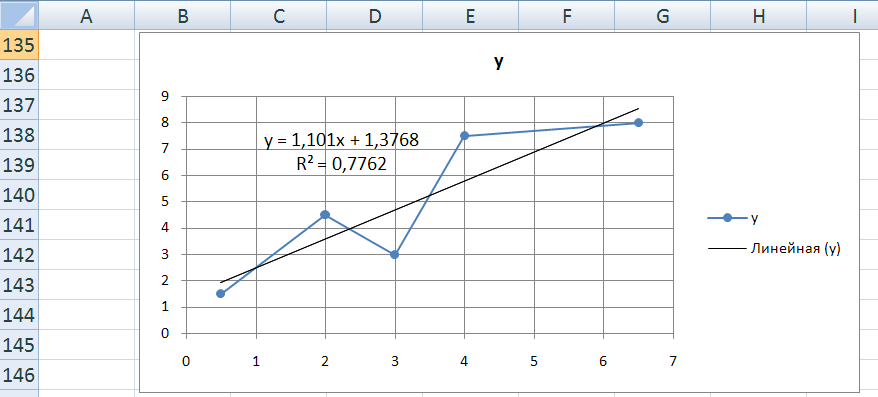
Рис. 7. Графики корреляционного поля и линии тренда с уравнением регрессии и коэффициентом детерминации.
Отформатировать график и сделать выводы по лабораторной работе.
Результаты работы предъявить преподавателю для выставления оценки.
Варианты задания.
Получена таблица значений контролируемой величины X и случайной величины Y. Найти уравнение линейной регрессии. Нанести на график исходные данные случайной величины Y и построить график линии регрессии.
Вариант 1.
|
xi |
0 |
0,1 |
0,2 |
0,3 |
0,4 |
|
yi |
16 |
17 |
13 |
11 |
14 |
Вариант 2.
|
xi |
0 |
0,1 |
0,2 |
0,3 |
0,4 |
|
yi |
16 |
18 |
11 |
13 |
11 |
Вариант 3.
|
xi |
0 |
0,1 |
0,2 |
0,3 |
0,4 |
|
yi |
19 |
12 |
15 |
12 |
13 |
Вариант 4.
|
xi |
0 |
0,1 |
0,2 |
0,3 |
0,4 |
|
yi |
19 |
12 |
15 |
12 |
13 |
Вариант 5.
|
xi |
5 |
10 |
15 |
20 |
25 |
|
yi |
6 |
10 |
19 |
21 |
29 |
Вариант 6.
|
xi |
1 |
2 |
3 |
4 |
5 |
|
yi |
16 |
17 |
12 |
14 |
11 |
Вариант 7.
|
xi |
1 |
2 |
3 |
4 |
5 |
|
yi |
11 |
14 |
12 |
17 |
16 |
Вариант 8.
|
xi |
1 |
2 |
3 |
4 |
5 |
|
yi |
12 |
13 |
17 |
14 |
16 |
Вариант 9.
|
xi |
1 |
2 |
3 |
4 |
5 |
|
yi |
19 |
15 |
17 |
14 |
16 |
Вариант 10.
|
xi |
1 |
2 |
3 |
4 |
5 |
|
yi |
7 |
4 |
7 |
3 |
6 |
Вариант 11.
|
xi |
1 |
2 |
3 |
4 |
5 |
|
yi |
6,5 |
5 |
6 |
4 |
5 |
Вариант 12.
|
xi |
1 |
2 |
3 |
4 |
5 |
|
yi |
4 |
4 |
5,5 |
5 |
7 |
Вариант 13.
|
xi |
2 |
3 |
4 |
5 |
6 |
|
yi |
4 |
5 |
5,5 |
5 |
8 |
Вариант 14.
|
xi |
2 |
3 |
4 |
5 |
6 |
|
yi |
3 |
6 |
5 |
5 |
7 |
Вариант 15.
|
xi |
1 |
2 |
3 |
4 |
5 |
|
yi |
18 |
13 |
11 |
14 |
10 |
Вариант 16.
|
xi |
0 |
0,1 |
0,2 |
0,3 |
0,4 |
|
yi |
16 |
17 |
13 |
11 |
14 |
Вариант 17.
|
xi |
0 |
0,1 |
0,2 |
0,3 |
0,4 |
|
yi |
16 |
18 |
11 |
13 |
11 |
Вариант 18.
|
xi |
5 |
6 |
8 |
9 |
10 |
|
yi |
16 |
17 |
12 |
14 |
11 |
Вариант 19.
|
xi |
1 |
2 |
3 |
4 |
5 |
|
yi |
11 |
14 |
12 |
17 |
16 |
