1. Выборочные оценки.

1. Выборочная оценка математического ожидания – выборочное среднее в Excel вычисляется с помощью функция СРЗНАЧ, при этом реализуется формула .

2. Оценка дисперсии – несмещенная (исправленная) выборочная дисперсияможет быть получена с помощью функцииДИСП. В Excel реализована формула .

3. Несмещенное выборочное средние квадратические отклонения (стандартное отклонение) вычисляется с помощью функции СТАНДОТКЛОН. Вычисления в Excel выполнены по формуле

.

4. Выборочная (смещенная) оценка дисперсии вычисляется с помощью функция ДИСПР.

Результат вычисления выборочных оценок , , и показан на рис.1.

… … … … … … …

Рис. 1. Фрагмент листа Excel с исходными данными и выборочными оценками параметров.

2. Описательная статистика.

Выполните процедуру Описательная статистика.

В главном меню Excel выбрать: Данные → Анализ данных → Описательная статистика → ОК.

В появившемся окне Описательная статистика ввести:

Входной интервал – 100 случайных чисел в ячейках $A$3: $A$102;

Группирование - по столбцам;

Выходной интервал – адрес ячейки, с которой начинается таблица Описательная статистика – например, $D$8;

Итоговая статистика – поставить галочку. ОК.

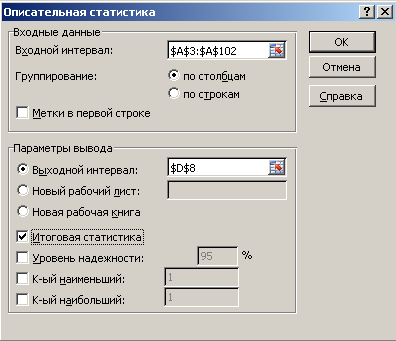
Рис. 2. Диалоговое окно Описательная статистика с заполненными полями ввода.

На листе Excel появится таблица – Столбец 1. В таблице даются все необходимые параметры, кроме моды Mo(X).

Рис. 3. Таблица Описательная статистика

Таблица содержит описательные статистики, в частности:

Среднее – оценка математического ожидания ;

Стандартное отклонение – оценка среднего квадратического отклонения;

Дисперсия – выборочная исправленная дисперсия ;

Эксцесс и Асимметричность – оценки эксцесса и асимметрии;

Медиана – оценка медианы;

Мода – оценка моды, #Н/Д – нет данных (наиболее часто встречающееся значение случайной величины в выборке).

Приблизительное равенство нулю оценок эксцесса и асимметрии, и приблизительное равенство оценки среднего оценке медианы дает предварительное основание выбрать в качестве основной гипотезы H₀ распределения элементов генеральной совокупности - нормальный закон.

Интервал – размах выборки;

Минимум – минимальное значение случайной величины в выборке ;

Максимум – максимальное значение случайной величины в выборке .

Результаты процедуры Описательная статистика потребуются в дальнейшем при построении теоретического закона распределения.

3. Построение гистограммы

В главном меню Excel выбрать Данные → Анализ данных → Гистограмма → ОК.

Далее необходимо заполнить поля ввода в диалоговом окне Гистограмма.

Входной интервал: 100 случайных чисел в ячейках $A$3: $A$102;

Интервал карманов: не заполнять;

Выходной интервал: адрес ячейки, с которой начинается вывод результатов процедуры Гистограмма;

Вывод графика – поставьте галочку.

Если поле ввода Интервал карманов не заполняется, то процедура вычисляет число интервалов группировки k и границы интервалов автоматически по формуле.

,

где, скобки означают – округление до целой части числа в меньшую сторону.

В рассматриваемом варианте n = 100, следовательно, k = 11. Действительно:

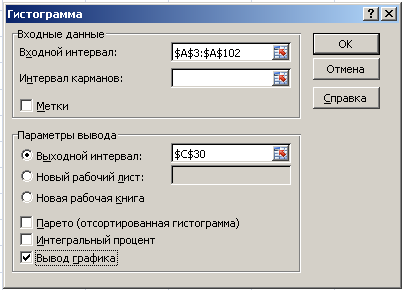
Рис. 4. Диалоговое окно Гистограмма.

В результате выполнения процедуры Гистограмма появляется таблица, содержащая границы x_i интервалов группировки (столбец – Карман) и частоту попадания случайных величин выборки m_i в i–ый интервал (столбец – Частота).

Справа от таблицы – график гистограммы.

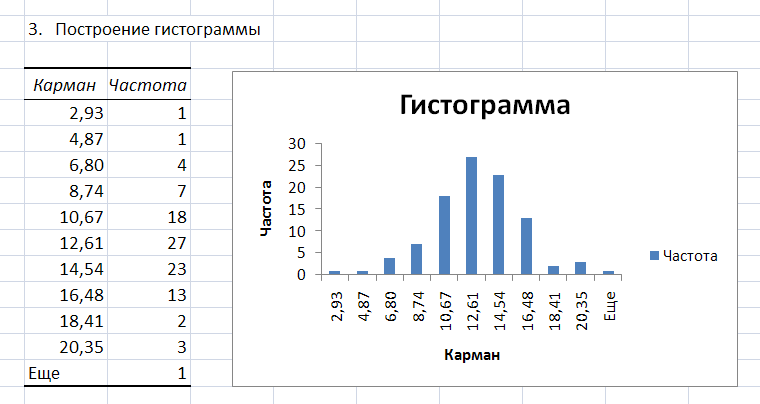
Рис. 5. Фрагмент листа Excel с результатами процедуры Гистограмма.

По виду гистограммы можно предположить (принять гипотезу) о том, что выборка случайных чисел подчиняется нормальному закону распределения.

Далее, для того чтобы убедиться в правильности выбранной гипотезы (по крайней мере визуально) надо, первое – построить график гипотетического нормального закона распределения, выбрав в качестве параметров (математического ожидания и среднего квадратического отклонении) их оценки (среднее и стандартное отклонение), и совместить график гипотетического распределения с графиком гистограммы.

И, второе – используя критерий согласия Пирсона установить справедливость выбранной гипотезы.