§ 68. Механические проявленияэлектрического поля.

Механические взаимодействия, наблюдаемые в электрическом поле между наэлектризованными телами и формально описываемые при помощи закона Кулона, могут быть объяснены, с точки зрения

216

Фарадея, как результат участия промежуточной среды во всех явлениях, происходящих в электрическом поле. По Фарадею, в диэлектрике, в котором вызвана электрическая деформация, суще­ствует тенденция к сокращению вдоль „линий индукции" (мы их называем линиями смещения), „сопровождаемая отталкивательными или рассеивающими силами в поперечном направлении". Поль­зуясь тем методом описания явлений, который мы применяли в предыдущих параграфах, мы можем сказать, следовательно, что фарадеевские трубки стремятся сократиться и при этом взаимно расталкиваются. Наличием в диэлектрике такого рода сил в полной мере объясняются все те притяжения и отталкивания, которые имеют место в системе наэлектризованных тел. В каждом частном случае, рассматривая схему расположения линий смещения или трубок смещения, не трудно сразу же определить общий характер тех движений, которые могут произойти в системе под действием электрической деформации среды.

Для того, чтобы рассчитать величину тяжения фарадеевских трубок, остановимся на случае, внешне аналогичном тому, что было принято в § 22 при рассмотре­нии тяжения магнитных линий. Представим себе две дисковые пластины, А иВ (рис. 125), расположенные параллельно одна другой. Допустим, что эти пла­стины заряжены равными по абсолютной величине и про­тивоположными по знаку зарядами.

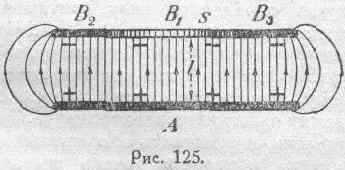
В центральной части промежутка между пластинами элек­трическое поле будет однородно, другими словами, фарадеевские трубки будут параллельны друг другу, и густота их будет постоянна. С целью получить возможность принимать во внимание только однородное поле, что упрощает все рассуждения, вырежем центральную часть верхнего диска, разделив его таким образом на две части: центральный диск В₁ с площадьюsи окружающее его охранное кольцоB₂B₃. Кольцо это называется охранным ввиду того, что оно принимает на себя все неравномерности электричес­кого поля по краям, где вследствие внутреннего распора в системе фарадеевских трубок они будут искривлены наружу. При этом предполагается, что потенциал частейВ₁ иВ₂В₃ один и тот же, так как они соединены, например, некоторым проводящим гибким про­водником. Теперь предположим, что дискА и охранное кольце?В₂В₃ закреплены неподвижно при помощи каких-либо изолирующих ча­стей, а дискВ₁ может перемешаться параллельно самому себе. В таком случае продольное тяжение фарадеевских трубок, заканчи­вающихся на дискеВ₁, будет стремиться сблизить дискиВ₁ иА, т. е. уменьшить расстояниеlмежду ними. Допуская, далее, что, благодаря этому, дискВ₁, опустился вниз наdl, и рассуждая затем совершенно подобно тому, как это мы сделали в § 22 примени­тельно к рис. 55, мы получим следующее выражение для силы тя-

217

жения f₁, рассчитанной на единицу поверхности поперечного сечения фарадеевских трубок:

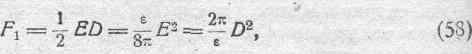
что в точности совпадает с величиной запаса электрической энергии, отнесенной к единице объема диэлектрика (см. соотношение 36 в § 67).

Расположение отдельных частей системы, изображенное на ри­сунке 125, вполне соответствует тому, что впервые применено было Кельвином (В. Томсоном) в его абсолютном электрометре, позволяющем измерять разность потенциалов без предварительной градуировки этого прибора путем сравнения его с каким-либо эта­лонным вольтметром. Именно Кельвин ввел охранное кольцо В₂В₃ для того, чтобы можно было просто рассчитать разность потен­циалов междуА иВ по силе притяженияb₁ кA. В оригинальных приборах Кельвина дискB₁подвешен к одному плечу коромысла весов. Нагружая соответственным образом другое плечо, можно без труда определить силу притяженияВ₁ кА при данной разности потенциалов между ними. А. А. Чернышев заключил такого рода систему в специальную камеру, в которую нагнетается воздух или какой-либо иной газ под давлением до 10 —15 атмосфер, благодаря чему значительно затрудняется образование разрядов через газ между пластинами электрометра. Таким образом, А. А. Чернышеву удалось осуществить абсолютный электрометр, позволяющий произ­водить измерения очень высоких напряжений, порядка сотен тысяч вольт. В виде примера приложения данных выше соотноше­ний (58) рассмотрим количественные зависимости, которыми можно пользоваться во время измерений при помощи абсолютного электрометра. Обозначая черезF полную силу тяження вниз дискаb₁ со стороны заканчивающихся на нем фарадеевских трубок, можем написать:

Ввиду однородности поля между А иВ₁ имеем:

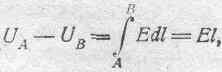
откуда:

Подставляя это в выражение для F, получаем:

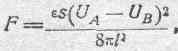
218

на основании чего приходим к следующему окончательному выводу:

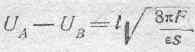
Если примем для воздуха =1, что в обычной практике вполне допустимо, то получим упрощенное численное соотношение:

Выражая F в динах,l— в сантиметрах иs— в квадратных сан­тиметрах, получим измеряемую разность потенциалов в абсолютных электростатических единицах, которые легко переводятся в вольты, так как каждая такая единица равна 300 вольтам (см. § 58).

Подобное использование представления о продольном тяжении фарадеевских трубок дает возможность и во многих других случаях рассчитать силы механического взаимодействия наэлектризованных частей системы. Это производится особенно просто, когда мы имеем дело с однородным полем, как это было в разобранном слу­чае (рис. 125).

Что касается величины поперечного распора, который имеет место в системе фарадеевских трубок, то Максвелл показал, что для равновесия элементарного объема диэлектрика необходимо, чтобы, кроме тяжений, существующих вдоль линий смещения, имело место еще и давление поперек линий смещения, выражающееся в случае пустоты, а также в случае жидких диэлектриков, совершенно по­добно тому, как и продольное тяжение. Таким образом, обозначай через f'₁ силу поперечного распора (давления) в системе фарадеевских трубок, рассчитанную на единицу поверхности, мы можем принять для пустоты и жидких диэлектриков: