
- •1. Основные понятия и определения электротехники. Топологические параметры.
- •2. Электронные осциллографы Электронные осциллографы
- •3. Эквивалентные схемы для источников энергии. Источники эдс и источники тока.
- •4. Цифровые измерительные приборы
- •5. Закон Ома для участка цепи с эдс
- •6. Аналоговые электронные вольтметры.
- •7. Расчет разветвленных магнитных цепей на основе закона Кирхгофа.
- •8. Приборы электродинамической и ферродинамической систем. Однофазный индукционный счетчик электрической цепи.
- •9. Расчет цепей постоянного тока при последовательном и параллельном соединении пассивных приемников.
- •10. Приборы магнитоэлектрической и электромагнитной схем. Магнитоэлектрическая система
- •Прибор магнитоэлектрической системы
- •Достоинства магнитоэлектрической системы
- •Недостатки магнитоэлектрической системы
- •Электромагнитная система
- •Прибор электромагнитной системы
- •Достоинства электромагнитной системы
- •Недостатки электромагнитной системы
- •11. Электрические цепи переменного тока, принципы получения переменной эдс.
- •12. Электрические измерения и приборы. Основные определения и термины. Методы измерений. Классификация средств измерений.
- •13. Действующие и среднее значения токов и напряжений в цепях переменного тока.
- •14. Цифро-аналоговые и аналогово-цифровые преобразователи.
- •15. Законы Ома и Кирхгофа для мгновенных значений токов и напряжений в цепях переменного тока.
- •16. Регистры, кольцевые счетчики. Счетчики с двоичным и недвоичным коэффициентами пересчета.
- •17. Расчет цепей переменного тока методом векторных диаграмм.
- •18. Последовательные цифровые устройства. Триггеры и их разновидности.
- •19. Расчет последовательных цепей переменного тока методом векторных диаграмм.
- •20. Комбинационные цифровые устройства. Мультиплексоры, демультиплексоры, дешифраторы, сумматоры.
- •21. Расчет параллельных цепей переменного тока методом векторных диаграмм.
- •22. Основные типы цифровых интегральных схем. Параметры цифровых ис.
- •23. Комплексный метод расчета параметров электрических цепей переменного тока.
- •24. Представление информации в цифровой форме. Составление логических функций и функциональных схем.
- •25. Явление резонанса в цепях переменного тока.
- •26. Транзисторные ключи на биполярных и полевых транзисторах. Аналоговые коммутаторы.
- •27. Трехфазные цепи переменного тока. Соединение приемников звездой и треугольником. Основные определения
- •2. Соединение в звезду. Схема, определения
- •3. Соединение в треугольник. Схема, определения
- •28. Импульсный режим работы электронных устройств. Генераторы импульса.
- •29. Нелинейные элементы электрических цепей и их характеристики. Графический метод расчета нелинейных цепей постоянного тока.
- •30. Генераторы гармонических колебаний.
- •2. Генератор lc-типа
- •31. Политический метод расчета нелинейных цепей.
- •32. Линейные преобразователи электрических сигналов на основе операционных усилителей
- •33. Магнитные цепи. Основные понятия и определения. Магнитный поток, индукция, напряженность. Магнитная проницаемость. Явление магнитного гистерезиса в веществе.
- •34. Методы расчета транзисторных усилителей.
- •35. Прямая и обратная задачи в расчетах магнитных цепей.
- •36. Усилители на транзисторах. Стабилизация начальной рабочей точки.
- •37. Уравнения Кирхгофа для магнитной цепи.
- •38. Классификация, основные параметры и характеристики усилителей. Обратная связь в усилителях.
- •39. Электромагнитные устройства. Принцип работы и основные аналитические соотношения для электромагнитов и электромагнитных реле.
- •40. Сглаживающие фильтры, стабилизаторы и инверторы в источниках вторичного электропитания.
- •41. Устройство и принцип работы трансформатора, его векторная диаграмма
- •Устройство и принцип работы
- •42. Выпрямительные схемы источников электропитания. Однополупериодные и двухполуперионые выпрямители.
- •43. Режим холостого хода трансформатора и его работа под нагрузкой.
- •44. Назначение и структура источников вторичного электропитания, их основные характеристики.
- •45. Устройство и принцип действия генератора постоянного тока эдс и электромагнитный момент. Способы возбуждения генераторов постоянного тока.
- •46. Операционные усилители, эквивалентная схема, основные характеристики и уравнения, интегральные микросхемы.
- •47. Двигатели постоянного тока. Регулирование скорости двигателей постоянного тока.
- •48. Основные свойтва, характеристики и типы тиринисторов. Динисторы и тринисторы.
- •49. Устройство и принцип работы асинхронного двигателя. Его характеристики.
- •50. Основные свойства, характеристики и типы полевых транзисторов.
- •51. Пуск и реверсирование асинхронных двигателей. Регулирование частоты вращения.
- •52. Устройство и принцип работы синхронного генератора. Его характеристики.
- •54. Основные свойства, характеристики и типы полупроводниковых диодов. Расчет электронных схем с диодами.
- •4.1.1. Выпрямление в диоде
- •4.1.2. Характеристическое сопротивление
- •4.1.4. Эквивалентная схема диода
- •55. Работа синхронной машины в режиме двигателя. Рабочие характеристики синхронного двигателя.
- •56.Краткие сведения о структуре полупроводников, электрические переходы в полупроводниках.
- •Свойства полупроводников.
- •Строение атомов полупроводников.
- •Электропроводность полупроводника.
- •Электронно-дырочная проводимость.
- •Электронная проводимость.
- •Дырочная проводимость.
15. Законы Ома и Кирхгофа для мгновенных значений токов и напряжений в цепях переменного тока.
Для мгновенных значений ЭДС, токов и напряжений остаются справедливыми сформулированные ранее законы Кирхгофа.
П е р в ы й: в любой момент времени алгебраическая сумма токов в узле электрической цепи равна нулю:
 ,
(2.8)
,
(2.8)
где n – число ветвей, сходящихся в узле.
В т о р о й: в любой момент времени в замкнутом контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме напряжений на всех остальных элементах контура:
 ,
(2.9)
,
(2.9)
где m – число ветвей, образующих контур.
Токи, напряжения и ЭДС, входящие в уравнения (2.8) и (2.9), есть синусоидальные функции времени, которые мы рассматриваем как проекции некоторых векторов на оси координат. Так как сложению проекций соответствует сложение векторов и соответствующих им комплексных чисел, то справедливыми будут следующие уравнения, которые можно записывать как для действующих, так и для амплитудных значений.
|
Законы Кирхгофа в векторной форме: |
Законы Кирхгофа в символической форме: |
|
|
|
Из сказанного вытекают три возможных подхода к расчету цепей синусоидального тока: выполнение операций непосредственно над синусоидальными функциями времени по уравнениям (2.8) и (2.9); применение метода векторных диаграмм, основанного на уравнениях (2.10), использование в расчетах комплексных чисел и уравнений (2.11), являющихся основой символического метода.
Пример 2.4. В узле электрической цепи сходятся три ветви (рис. 2.14).
|
Токи первых двух ветвей известны: i1 = 8sin(w t+30° ) А, i2 = 6sin(w t+120° ) А. Требуется записать выражение тока i3 и определить показания амперметров электромагнитной системы. |
Рис. 2.14. Узел электрической цепи |
16. Регистры, кольцевые счетчики. Счетчики с двоичным и недвоичным коэффициентами пересчета.



Счетчиком называется автомат, выполняющий функции подсчета количества импульсов единичных сигналов, поступивших на его вход, а также функции формирования и запоминания некоторого двоичного кода, соответствующего этому количеству. Другими словами - счетчик является преобразователем число-импульсного кода в некоторый двоичный код.
Помимо указанных функций счетчики иногда также могут выполнять функции приема и выдачи кода.
Входными сигналами счетчика являются или сигнал суммирующего или вычитающего счета, при этом одновременная подача этих сигналов запрещена.
В качестве выходной функции счетчика может быть задан сигнал переполнения, возникающий при суммировании, или сигнал заема возникающий при вычитании во время перехода счетчика через нуль.
Основным результатом работы счетчика является накопленный в нем код, определяемый состояниями элементарных автоматов.
Число элементарных автоматов (триггеров), необходимых для построения счетчика с заданным коэффициентом пересчета, равно числу его разрядов и определяется по формуле
m = log2N, (1)
где N - коэффициент пересчета (модуль, период счетчика) - максимальное число внутренних состояний, которое должен иметь счетчик. Очевидно, что это число равно максимальному числу входных сигналов, которое может сосчитать счетчик.
К другим важнейшим характеристикам счетчика относятся:
1) время регистрации - это интервал времени между поступлением входного сигнала и окончания самого длинного переходного процесса в схеме;
2) разрешающая способность - минимально допустимый период следования входных сигналов, при котором счетчик работает без сбоев.
2.2 Классификация счетчиков
Схемы счетчиков можно классифицировать по следующим признакам:
1) По основанию системы счисления счетчики делятся на:
а) двоичные ;
б) десятичные (двоично- десятичные);
Двоичные счетчики в свою очередь подразделяются на счетчики, модуль пересчета которых не равен 2m (где m - разрядность счетчика). Последние называются счетчиками по модулю М ( где М - число не кратное степени двойки ) .
2) По направлению переходов счетчики принято подразделять на:
а) суммирующие ;
б) вычитающие ;
в) реверсивные.
К последним относятся счетчики, способные выполнять операции суммирования и вычитания.
3) По способу построения цепей сигналов переноса различают счетчики:
а) с последовательным переносом ;
б) со сквозным переносом ;
в) с параллельным (сквозным) переносом ;
г) с частично групповым переносом .
4) По способу организации счета счетчики подразделяют на:
а) синхронные ;
б) асинхронные.
Время установки кода tуст является основным фактором, определяющим выбор способа переключения триггеров. При асинхронном способе tуст растет с увеличением числа триггеров (m) в счетчике, а при синхронном способе tуст не зависит от величины m.
Следует также учитывать, что с триггеров счетчика снимаемый параллельный код иногда подается на комбинационную схему (например, на дешифратор). В этом случае при асинхронном способе из-за неодновременного срабатывания триггеров счетчика возможно появление ложных логических сигналов на выходах комбинационной схемы.
Поэтому более предпочтительным, как правило, является синхронный способ организации счета, хотя при его использовании в счетчиках с большим числом триггеров (m>5..10) предъявляются повышенные требования к нагрузочной способности источников синхро-сигналов.
Асинхронный способ целесообразно применять в счетчиках, используемых в качестве делителей частоты.
Некоторые счетчики имеют цепи внешней установки начального состояния. Это состояние может также устанавливаться с помощью цепей обратной связи, имеющихся в самом счетчике. Кроме этого, счетчик может устанавливаться в начальное состояние после завершения одного цикла работы - подсчета числа входных сигналов, равного модулю счетчика.
2.3 Принцип работы счетчиков
Анализ схем счетчиков удобно начать с рассмотрения асинхронного двоичного счетчика с последовательным переносом (рисунок 1,а). Состояния триггеров счетчика после воздействия серии входных импульсов приведены в таблице 1. Временная диаграмма счетчика показана на рисунке 1,б.
Коэффициент пересчета этого счетчика
4 = log2Kсч; Ксч = 24 = 16.
В качестве элементарного автомата используем Т-триггер. Эти счетчики характеризуются тем, что управляющими сигналами для старших разрядов являются сигналы, снимаемые с информационных выходов младших разрядов.
В исходном состоянии все триггеры устанавливаются в ноль (чтобы не загромождать чертеж, цепи сброса не показаны). В этом случае на нижних выводах всех триггеров устанавливается логическая еденица, а на верхних - логический ноль.
При поступлении импульса счета (рисунок 1,б) первый разряд подготовится к переключению и после окончания импульса перейдет в состояние Q = 1. Сигнал единица подается на вход второго триггера. После окончания действия второго счетного импульса на вход второго триггера поступит отрицательный перепад напряжения, так как первый триггер из состояния Q1=1 перейдет в состояние ноль.
Этот перепад напряжения вызовет изменение состояния второго триггера из нуля в единицу и на его выходе, а следовательно, на входе третьего триггера будет высокий потенциал. Сигнал Q2=1 подготавливает срабатывание третьего триггера. При поступлении семи импульсов установится состояние Q1=Q2=Q3=1, а восьмой импульс последовательно переключит все эти триггеры в состояние ноль и схема перейдет в первоначальное состояние.
Подобные счетчики являются простейшими по схемной реализации, но имеют невысокое быстродействие. Быстродействие счетчиков обычно характеризуется временем установки и максимальной частотой поступления счетных импульсов.

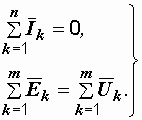 (2.10)
(2.10) (2.11)
(2.11)