Стукалов-Русских / Лабораторная раб. 2

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Омский государственный педагогический университет»

Факультет математики, информатики, физики и технологии

Кафедра прикладной математики

Лабораторная работа №2

по дисциплине «Численные методы»

Выполнил: студент

33 группы

Русских Юрий Вячеславович

_______________________

(подпись)

Проверил:

Стукалов Виктор Анатольевич

к.п.н., доцент

Оценка ________________

«___» _______________ 20___г.

_______________________

(подпись)

Омск, 2013

Задание 1: Найти корни заданного уравнения графическим способом. Написать программу для метода табулирования.

Решение:

x	y
-4,2	-0,10244
-4,1	0,023456
-1,7	0,08954
-1,6	-0,00357
1,5	-0,04374
1,6	0,061968

Найдем корни с помощью метода табулирования.

program Separat_root;

uses crt;

var a,b,x1,x2,y1,y2,h:real; n,k:integer;

function f(x:real):real; {уравнение вида F(x)=0}

begin f:=(0,2*x)^3-cos(x);

end;

begin

clrscr;

writeln('Vvedite a,b,h'); read(a,b,h);

k:=0; x1:=a; x2:=x1+h; y1:=f(x1);

while x2<b do

begin y2:=f(x2);

if y1*y2<0 then

begin inc(k);

writeln (k,'koren [',x1:4:1, ';',x2:4:1, ']')

end;

x1:=x2; x2:=x1+h; y1:=y2;

end;

repeat until keypressed

end.

Задание 2: По методу половинного деления вычислить один корень заданного уравнения с точностью 0,5*10^-4, с помощью программы.

Метод половинного деления.

program divide_half;

uses crt,okrugl;

type T=real;

var a,b,c,eps,x:T; n,m:integer;

function f(x:T):T;

begin f:= (0,2*x)^3-cos(x);

end;

begin

clrscr;

writeln('Vvedite a,b,eps');

read(a,b,eps);

repeat

c:=(a+b)/2;

if f(a)*f(c)<0 then b:=c else a:=c;

until b-a<=eps;

x:=(a+b)/2; okr(x,eps,x,n);

if x<0 then begin if n<0 then m:=0 else m:=n;

writeln('x=',x-1E-10:7:m,' n=',n)

end

else begin if n<0 then m:=0 else m:=n;

writeln('x=',x+1E-10:7:m,' n= ',n)

end;

repeat until keypressed

end.

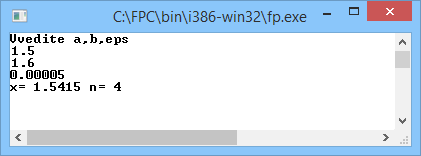
Проверка:

Х=(0,2*1,5415)^3-cos(1,5415)= 1,14365*10^-5

Задание 3: Вычислить корень заданного уравнения, используя датчик случайных чисел и золотое сечение.

Метод датчика случайных чисел.

program VK;

uses crt, okr;

type T=real;

var a,b,c,eps,x:T; n,m:integer;

function f(x:T):T;

begin f:=(0,2*x)^3-cos(x);

end;

begin

clrscr;

writeln('Введите a,b,eps');

read(a,b,eps);

repeat

randomize;

c:=a+(b-a)* Random;

if f(a)*f(c)<0 then b:=c else a:=c;

until b-a<=eps;

x:=(a+b)/2; okr(x,eps,x,n);

if x<0 then begin if n<0 then m:=0 else m:=n;

writeln('x=',x-1E-10:7:m,' n=',n)

end

else begin if n<0 then m:=0 else m:=n;

writeln('x=',x+1E-10:7:m,' n= ',n)

end;

repeat until keypressed

end.

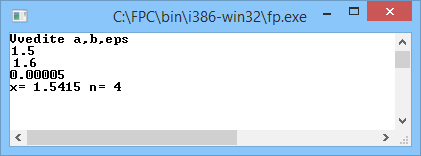
Проверка:

Х=(0,2*1,5415)^3-cos(1,5415)= 1,14365*10^-5

Метод золотого сечения.

program zoloto;

uses crt, okr;

type T=real;

var a,b,c,eps,x:T; n,m:integer;

function f(x:T):T;

begin f:=(0,2*x)^3-cos(x);

end;

begin

clrscr;

writeln('Введите a,b,eps');

read(a,b,eps);

repeat

c:=((b-a)-(((sqrt(5)-1)*(b-a))/2))+a;

if f(a)*f(c)<0 then b:=c else a:=c;

until b-a<=eps;

x:=(a+b)/2; okr(x,eps,x,n);

if x<0 then begin if n<0 then m:=0 else m:=n;

writeln('x=',x-1E-10:7:m,' n=',n)

end

else begin if n<0 then m:=0 else m:=n;

writeln('x=',x+1E-10:7:m,' n= ',n)

end;

repeat until keypressed

end.

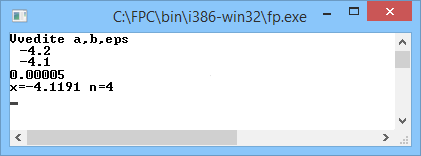
Проверка:

Х=(0,2*-4,1191)^3-cos(-4,1191)= -1,87007*10^-5

Задание 4: Вычислить корень заданного уравнения методом простой итерации.

Приведем уравнение (0,2*x)^3-cos(x) к виду x=f(x).

х:=х – μ * F(x)

х:=х – μ * ((0,2*x)^3-cos(x))

Найдем производные функции F(x)= (0,2*x)^3-cos(x)

F`(x) = 0.024*x^2+sin(x)

F`(1,5)= 1,0514>0

F`(1.6)= 1,0610>0

M=max| F`(x)|

M=1,0610

=1/M=1/1,0610=0,943

Получаем итерационную формулу:

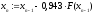
Для использования критерия выхода из итерационного процесса найдем q.

q=1-m/M, где m=min| F`(x)|= 1,0514

q=1-1,0514/1,0610=0,009048

Малое значение q обеспечивает быструю сходимость итерационной последовательности.

Выберем x₀=-1,7 и сделаем несколько итераций.

n	Xn	Xn+1=Xn-0,943*((0,2*Xn)^3-cos(Xn))	q/(1-q)*(Xn+1-Xn)
1	1.5	1,541244	0,009131
2	1,541244	1,541488	0,009131
3	1,541488	1,541489	0,009131

F(1,541244)= (0,2*1,541244)^3-cos(1,541244) = -2,6*10^-4

F(1,541488)= (0,2*1,541488)^3-cos(1,541488) = -1,2*10^-6

Ответ: х=1,541488, т.к. F(1,541488)= (0,2*1,541488)^3-cos(1,541488) = -1,2*10^-6 меньше, чем заданная точность.