
- •Глава I. Элементы теории множеств
- •Вопросы для самопроверки
- •Разберите решения следующих примеров
- •Задачи для самостоятельного решения
- •Глава II. Алгебра высказываний
- •Вопросы для самопроверки
- •Разберите решение следующих примеров
- •Приложения алгебры высказываний
- •Задачи для самостоятельного решения
- •Глава III. Алгебра предикатов
- •Вопросы для самопроверки
- •Разберите решения следующих примеров
- •Задачи для самостоятельного решения
- •Глава IV. Бинарные отношения
- •Вопросы для самопроверки
- •Разберите решения следующих примеров
- •Задачи для самостоятельного решения
- •Глава V. Элементы комбинаторики
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
Глава III. Алгебра предикатов
Л.М.Мартынов. Вводный курс математики, стр.43-69
Вопросы для самопроверки
1. Какое множество связано с каждой предметной переменной?
2. Укажите переменные и их области допустимых значений в предложениях:
a) «Число больше своей целой части».
б) «Река впадает в море».
в) «Точка лежит на стороне квадрата».
г) «Два треугольника подобны».
д) «Человек идёт по свету».
3. Как записывается предложение с переменными x, y, z и со свойством Р ?
4.
Какие истинностные значения принимает
предикат
![]() на наборах (1;3) и (4;2) значений предметных
переменных?
на наборах (1;3) и (4;2) значений предметных
переменных?
5.
Найдите область истинности предиката
![]() наR?
наR?
6.
Если
![]() ,
то каковы значения высказываний
,
то каковы значения высказываний![]()
7.
Каким свойством обладает таблица
истинности предиката
![]() с
натуральными переменными, если
с
натуральными переменными, если![]() принимает истинное значение при каждом
натуральномy?
принимает истинное значение при каждом
натуральномy?
8.
Каковы истинностные значения высказываний,
еcли
вcе
участвующие в их записи переменные
являются натуральными
![]() ?
?
9.
Можно ли в формуле
![]() записать
кванторы в обратном порядке:
записать
кванторы в обратном порядке:![]() ?
?
10.
Верно ли что при действительном х
имеет место
![]()
11.Справедливо
ли при действительном х
:
![]()
12.
Верна ли при натуральном х
равносильность
![]()
13. Будут ли формулами алгебры предикатов записи:
![]() 14.
Как выглядит отрицание
14.
Как выглядит отрицание
![]() – согласно законам отрицания кванторов?
– согласно законам отрицания кванторов?
15. Верно ли:
![]()
16.
Почему справедливо
![]()
17.
Как записать утверждение, обратное
![]()
18.
Запишите без ограниченных кванторов:
![]()
19.
Запишите с ограниченными кванторами:
![]() .
.
20.
Почему формула
![]() является
тождественно истинной?
является
тождественно истинной?
Разберите решения следующих примеров
П р и м е р 1. Предложение: «Человек х — поэт» является предикатом. Сказуемое здесь: «быть поэтом».
Если предложение содержит одну переменную, оно называется одноместным предикатом.
Для обозначения одноместных предикатов используют символы: А(х), В(х), Р(х), Q2(х) и так далее.
Слово «предикат» происходит от латинского «ргеdicate» (сказуемое).
П р и м е р 2. Рассмотрим предложение: «2х–4 > 0». Истинно оно или ложно? Мы не можем ответить на этот вопрос. Это не есть высказывание. Но если вместо х поставить некоторое число, например 3, то мы получим истинное высказывание: «2 ∙ 3 – 4 > 0». Если вместо х поставить 1, то мы получим ложное высказывание: «2 ∙ 1 – 4 > 0». Исходное предложение содержит букву х и при подстановке вместо х некоторого числа, получаем высказывание. Данное предложение является одноместным предикатом.
Множество значений X которое принимает переменная х, называется областью определения предиката А(х).
Совокупность Т
значений переменной х,
при которых предикат А(х),
![]() принимает истинные значения, называетсямножеством
истинности предиката
А(х).
принимает истинные значения, называетсямножеством
истинности предиката
А(х).
В примере 2 область
определения X = R,
а область истинности
![]()
П р и м е р 3.
а)
![]()
б)
![]()
в)
![]() множество
простых чисел;
множество
простых чисел;
г)
![]() .
В школе обычно говорят о множестве
корней уравнения. Это то же самое, что
и множество истинности соответствующего
предиката.
.
В школе обычно говорят о множестве
корней уравнения. Это то же самое, что
и множество истинности соответствующего
предиката.
Замечание. Область определения Х любого одноместного предиката А(х) можно разбить на два подмножества. Одно из них – область истинности Т предиката А(х), другое подмножество является дополнением множества Т до всего множества Х (Рис. 14).
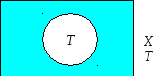
Рис.14
Если множество истинности предиката совпадает с его областью определения, то такой предикат называется тождественно истинным. Если множество истинности предиката пусто, то такой предикат называется тождественно ложным.
П р и м е р 4. а) На
множестве действительных чисел предикат
![]() является тождественно истинным (его
область определения и множество
истинности одинаковы:X
= Т = R);
является тождественно истинным (его
область определения и множество
истинности одинаковы:X
= Т = R);
б) На множестве
действительных чисел предикат «
| х | < 0»
является тождественно ложным, так как
его множество истинности
![]() .
.
Два предиката А(х) и В(х), заданные на одном и том же множестве X, имеющие одинаковые множества истинности называются эквивалентными (логически равносильными или логически равными).
Пишут:
![]() (предикатыА(х)
и В(х)
эквивалентны).
(предикатыА(х)
и В(х)
эквивалентны).
П р и м е р 5. а)
![]() «Натуральное число х делится на 3»,
«Натуральное число х делится на 3»,![]() «Сумма цифр десятичной записи натурального
числа х делится на 3»,
«Сумма цифр десятичной записи натурального
числа х делится на 3»,![]() ,
так как множеством истинности каждого
из этих предикатов является:
,
так как множеством истинности каждого
из этих предикатов является:![]()
б)![]()
![]() так как множество истинности этих
предикатов является
так как множество истинности этих
предикатов является![]()
в)
![]() ,
так как множеством истинности каждого
из этих предикатов является:
,
так как множеством истинности каждого
из этих предикатов является:![]()
Каждый одноместный
предикат А(х)
можно превратить в высказывание с
помощью логической операции квантификации
– навешивание
квантора общности
![]() и квантора существования
и квантора существования![]() :
:
![]() читается
«для любого икс а от икс»,
читается
«для любого икс а от икс»,
![]() читается «существует
икс а от икс»
читается «существует
икс а от икс»
Замечание 1 . Записи
![]() и
и
![]() можно
читать по-разному, хотя их логический
смысл всегда один и тот же. Наиболее
употребительные из них следующие (слова
в квадратных скобках иногда опускаются):
можно
читать по-разному, хотя их логический
смысл всегда один и тот же. Наиболее
употребительные из них следующие (слова
в квадратных скобках иногда опускаются):
1.
![]() читается
так:
читается
так:
а) для любого (всякого, каждого [значения]) х из Х А(х) [истинно];
б) всякий (любой, каждый) элемент х из множества X обладает свойством А(х);
в) Каково бы ни было х из X, А(х).
2.
![]() читается так:
читается так:
а) существует [значение] х из Х такое, что А(х) [истинно];
б) для некоторых [значений] х из X А(х) [истинно];
в) по меньшей мере (хотя бы) одно [значение] х из Х таково, что А(х) [истинно];
г) найдётся такое x: из X, чтo А(х) [истинно].
Слово «квантор»
происходит от латинского слова «quantum»,
что означает «сколько». Обозначения
![]() и
и
![]() произошли от первых букв английских
слов «All»
– все и «Exist»
– существует.
произошли от первых букв английских
слов «All»
– все и «Exist»
– существует.
Высказывание
![]() считается истинным, если свойством А
обладают все элементы (обладает хотя
бы один элемент) из области определения
предиката А(х),
другими словами, если множество истинности
Т
предиката А(х)
совпадает с его областью определения
считается истинным, если свойством А
обладают все элементы (обладает хотя
бы один элемент) из области определения
предиката А(х),
другими словами, если множество истинности
Т
предиката А(х)
совпадает с его областью определения
![]()
П р и м е р 6. а)
Предикат
![]() превращается
в истинное высказывание, если
воспользоваться квантором общности:
превращается
в истинное высказывание, если
воспользоваться квантором общности:
![]() (читается так: для всех действительных
значений х
выполняется неравенство
(читается так: для всех действительных
значений х
выполняется неравенство
![]() ).
Здесь
).
Здесь
![]()
б) Предикат
![]() превращается
в истинное высказывание с помощью
квантора существования:
превращается
в истинное высказывание с помощью
квантора существования:
![]() (читается
так: существует действительное значение
х
такое, что
(читается
так: существует действительное значение
х
такое, что
![]() .
В этом случае
.
В этом случае
![]()
П р и м е р 7. Прочитайте следующие высказывания. Какие из них истинны и почему?
а)
![]()
б)
![]()
в)
![]()
Решение.
а)![]() (читается
так: при любом действительном х
имеем х + 3 =
8). Это
высказывание ложно, так как, например,
при х = 4
имеем:
(читается
так: при любом действительном х
имеем х + 3 =
8). Это
высказывание ложно, так как, например,
при х = 4
имеем:
![]()
б)![]() (читается так: существует действительное
значение х
такое, что х
+ 3 = 8). Это
высказывание истинно, так как
(читается так: существует действительное
значение х
такое, что х
+ 3 = 8). Это
высказывание истинно, так как
![]()
в)![]() (читается так: существует действительное
число х,
квадрат которого отрицателен). Это
высказывание ложно, так как
(читается так: существует действительное
число х,
квадрат которого отрицателен). Это
высказывание ложно, так как
![]() .
.
П р и м е р 8. Запишите следующие высказывания, используя кванторы:
а) «Квадрат любого числа есть число неотрицательное»;
б) «Найдётся такое действительное х, квадрат которого равен 0 ».
Ответ: а)![]() ;
б)
;
б)![]() .
.
Замечание 2.
Навешивание кванторов можно применить
к любому предикату, при этом получится
истинное или ложное высказывание. Если
область определения предиката А(х)
конечна и равна
![]() ,
то имеют место логические равенства:
,
то имеют место логические равенства:
![]()
![]()
П р и м е р 9. а) На
множестве
![]() задан предикат
задан предикат![]() .
Высказывание
.
Высказывание
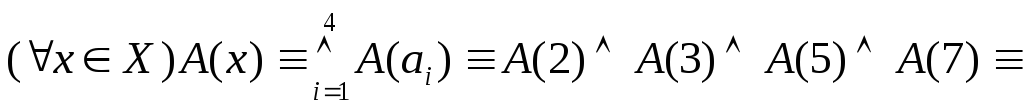
![]() (истинное
высказывание);
(истинное
высказывание);
б)
На множестве![]() задан предикат
задан предикат![]() .
.
Высказывание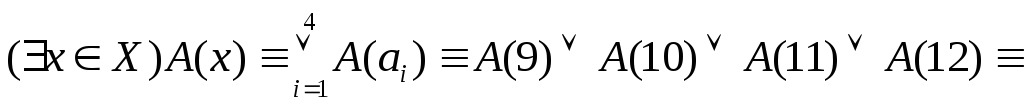
![]() (истинное
высказывание).
(истинное
высказывание).
Предикат может
содержать более одного переменного.
Тогда он называется двуместным,
трёхместным
и т.д. по числу переменных. И кванторов
может быть несколько. Для обозначения
двуместных предикатов используют
символы А(х,
у), В(х, у) и
так далее. к-местные
предикаты обозначаются так:
![]()
![]() и так далее.
и так далее.
П р и м е р 10. а)![]() – двуместный предикат;
– двуместный предикат;
![]() –истинное
высказывание.
–истинное
высказывание.
б)
![]() – истинное высказывание, сокращённо
пишут так:
– истинное высказывание, сокращённо
пишут так:![]()
П р и м е р 11.
![]() – истина.
– истина.
![]() –ложь.
–ложь.
То есть разноименные кванторы нельзя переставлять. Следует отметить, что одноименные кванторы можно переставлять.
П р и м е р 12.(![]() где
где![]() – точки плоскости)
– точки плоскости)![]() истинное высказывание.
истинное высказывание.
Предикаты, так же как и высказывания бывают простыми (элементарными) и составными (сложными). Составные предикаты образуются из простых при помощи логических связок: «и», «или», «неверно, что», «если..., то...», «тогда и только тогда», смысл которых тот же, что и в логике высказываний. Дадим определение логических операций над предикатами.
Отрицанием
предиката
![]() называют предикат
называют предикат![]() ,
истинный при тех и только тех значениях
из множества X,
при которых предикат А(х)
– ложен, и
наоборот.
,
истинный при тех и только тех значениях
из множества X,
при которых предикат А(х)
– ложен, и
наоборот.
П р и м е р 13.
![]() «Число x
оканчивается цифрой 5».
«Число x
оканчивается цифрой 5».
![]() «Неверно, что числох
оканчивается цифрой 5» (или «Число х
не оканчивается цифрой 5»), Т
= {15, 25} —
множество истинности А(х).
«Неверно, что числох
оканчивается цифрой 5» (или «Число х
не оканчивается цифрой 5»), Т
= {15, 25} —
множество истинности А(х).
![]() {10, 20, 30} –
множество истинности
{10, 20, 30} –
множество истинности
![]() .
На рисунке 15 множество
.
На рисунке 15 множество![]() (дополнение множестваТ
до X)
заштриховано.
(дополнение множестваТ
до X)
заштриховано.
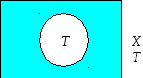
Рис.15
Отрицание
кванторов.
Сравним два высказывания:
![]() и
и![]() .
Первое означает: «Не для всех значенийх
истинно А(х).»
Второе означает: «Существует такое
значение х,
для которого неверно А(х).»
Оба высказывания имеют одинаковый
смысл, поэтому имеем:
.
Первое означает: «Не для всех значенийх
истинно А(х).»
Второе означает: «Существует такое
значение х,
для которого неверно А(х).»
Оба высказывания имеют одинаковый
смысл, поэтому имеем:
![]() (1).
(1).
Аналогично,
получаем:
![]() (2).
(2).
В самом деле, левая часть (2) означает: не существует такого значения х, для которого истинно высказывание А(х). Справа: А(х) ложно для всех значений х. Равносильность (1) и (2) называются законами де-Моргана для кванторов.
Итак, чтобы отрицать некоторый квантор, достаточно заменить его на квантор другого смысла, а отрицание перенести на предикат, стоящий за квантором.
П р и м е р 14.
![]() .
.
П р и м е р 15.
![]()
Замечание. Повторяя последовательно эти законы, можно «раскрыть» отрицание нескольких кванторов. Например:
![]() .
.
П р и м е р 16. Функция
f(х)
называется ограниченной на множестве
X,
если
![]() .
Составим отрицание этого определения,
получим определение неограниченной
функции:
.
Составим отрицание этого определения,
получим определение неограниченной
функции:![]() .
.
Конъюнкцией
предикатов
А(х)
и В(х),
заданных на множестве X
называется предикат
![]() истинный
при тех и только техх
из X,
при которых истинны оба предиката А(х)
и В(х).
истинный
при тех и только техх
из X,
при которых истинны оба предиката А(х)
и В(х).
П р и м е р 17.
![]() «Числоx
кратно 3», его множество истинности
«Числоx
кратно 3», его множество истинности
![]() «Числох
кратно 5», его область истинности
«Числох
кратно 5», его область истинности
![]()
![]() «Число х кратно 3 и 5», его множество
истинности
«Число х кратно 3 и 5», его множество
истинности![]() (на рисунке 16 множество
Т заштриховано).
(на рисунке 16 множество
Т заштриховано).
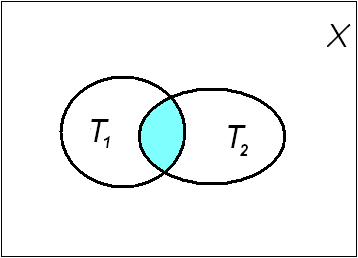
Рис. 16
Дизъюнкцией
предикатов
А(х)
и В(х),
заданных на множестве X
называется предикат
![]() ложный
при тех и только техх
из Х
при которых ложны оба предиката А(х)
и В(х).
ложный
при тех и только техх
из Х
при которых ложны оба предиката А(х)
и В(х).
П р и м е р 18.
![]() .
.![]() «Числох
кратно 3», его область истинности
«Числох
кратно 3», его область истинности
![]()
![]() «Числох
кратно 5», его множество истинности
«Числох
кратно 5», его множество истинности
![]()
![]() «Числох
кратно 3 или 5»; множеством истинности
дизъюнкции предикатов является
множество
«Числох
кратно 3 или 5»; множеством истинности
дизъюнкции предикатов является
множество
![]() (Рис. 17).
(Рис. 17).
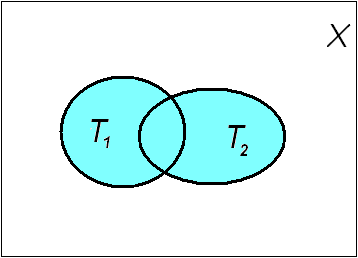
Рис. 17
Импликацией
предикатов А(х)
и
В(х), заданных
на множестве X
называется предикат
![]() ложный при тех и только техх
из X,
при которых предикат А(х)
истинен, а В(х)
ложен.
ложный при тех и только техх
из X,
при которых предикат А(х)
истинен, а В(х)
ложен.
П р и м е р 19.
![]() .
.![]() «Числох
кратно 3», его множество истинности
«Числох
кратно 3», его множество истинности
![]()
![]() «Числох
кратно 5», его множество истинности
«Числох
кратно 5», его множество истинности
![]()
![]() «Если числох
кратно 3, то оно кратно 5»; множеством
истинности импликации предикатов
является множество
«Если числох
кратно 3, то оно кратно 5»; множеством
истинности импликации предикатов
является множество
![]() (Рис.18).
(Рис.18).
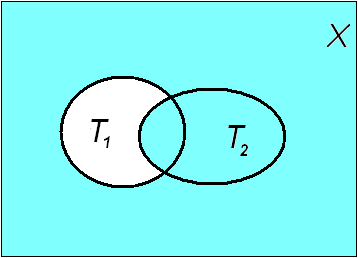
Рис. 18
Если истинно
высказывание
![]() ,
то предикатВ(х)
называется логическим
следствием А(х)
(или следствием А(х)).
,
то предикатВ(х)
называется логическим
следствием А(х)
(или следствием А(х)).
П р и м е р 20.
Рассмотрим два уравнения (два одноместных
предиката):
![]() (1) и
(1) и![]() (2). В качестве области определения
выберем множествоR.
(множество действительных чисел).
Высказывание
(2). В качестве области определения
выберем множествоR.
(множество действительных чисел).
Высказывание
![]() истинно,
поэтому уравнение (2) является логическим
следствием уравнения (1).
истинно,
поэтому уравнение (2) является логическим
следствием уравнения (1).
Замечание. Запись
![]() (с пропуском квантора встречается и в
математической литературе).
(с пропуском квантора встречается и в
математической литературе).
П р и м е р 21.
![]() .
.![]() «Числох
делится на 4», его область истинности
«Числох
делится на 4», его область истинности
![]() ;
;![]() «Числох
делится на 2», его область истинности
«Числох
делится на 2», его область истинности
![]() .
Из истинностиА(х)
следует истинность В(х),
то есть
.
Из истинностиА(х)
следует истинность В(х),
то есть
![]() .
Заметим, что
.
Заметим, что![]() (множество, на котором предикат
(множество, на котором предикат![]() принимает ложные значения пусто). Кроме
того,
принимает ложные значения пусто). Кроме
того,![]() .
.
Итак, высказывание
![]() истинно в том и только том случае, когда
истинно в том и только том случае, когда![]() (множество истинности
(множество истинности![]() предикатаА(х)
содержится в множестве истинности
предиката В(х)).
предикатаА(х)
содержится в множестве истинности
предиката В(х)).
Эквиваленцией
предикатов
А(х) и
В(х), заданных
на множестве X
называется предикат
![]() истинный
при тех и только техх
из X,
при которых оба предиката А(х)
и
В(х) становятся
истинными и ложными одновременно.
истинный
при тех и только техх
из X,
при которых оба предиката А(х)
и
В(х) становятся
истинными и ложными одновременно.
П р и м е р 22.
![]() .
.![]() «Числох
кратно 3», его множество истинности
«Числох
кратно 3», его множество истинности
![]()
![]() «Числох
кратно 5», его множество истинности
«Числох
кратно 5», его множество истинности
![]() .
.![]() «Числох
кратно 3, тогда и только тогда, когда х
кратно 5». Оба предиката одновременно
истинны или ложны при
«Числох
кратно 3, тогда и только тогда, когда х
кратно 5». Оба предиката одновременно
истинны или ложны при
![]() ,
поэтому множество истинности эквиваленции
предикатов есть множество
,
поэтому множество истинности эквиваленции
предикатов есть множество![]() .
Очевидно, что
.
Очевидно, что![]() (Рис.19)
.
(Рис.19)
.
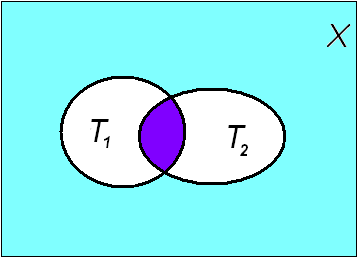
Рис. 19
Замечание. Можно
дать ещё одно определение равносильности
предикатов: предикаты
![]() и
и![]() ,
,![]() называются
эквивалентными (логически равносильными
или логически равными), если истинно
высказывание
называются
эквивалентными (логически равносильными
или логически равными), если истинно
высказывание![]() .
.
П
1 Л 2 И 3 И 4 Л --- ---
![]()
![]()
![]() ,
заданный предложением «Натуральноех
является простым числом», имеет
натуральную переменную. Для первых
натуральных значений переменой значения
,
заданный предложением «Натуральноех
является простым числом», имеет
натуральную переменную. Для первых
натуральных значений переменой значения
![]() можно вписать так, как в таблице справа.
При необходимости такую таблицу
продолжают строить и дальше. Аналогично,
для предиката
можно вписать так, как в таблице справа.
При необходимости такую таблицу
продолжают строить и дальше. Аналогично,
для предиката![]() заданного предложением «Натуральноех делится
на натуральное у»,
можно построить начало двухмерной
таблицы истинности так, как это сделано
справа. Из начала этой таблицы видно,
что, например,
заданного предложением «Натуральноех делится
на натуральное у»,
можно построить начало двухмерной
таблицы истинности так, как это сделано
справа. Из начала этой таблицы видно,
что, например,
![]() – Л, а
– Л, а![]() – И.
– И.
П
1 2 3 4 5 6 … 1 И Л Л Л Л Л … 2 И И Л Л Л Л … 3 И Л И Л Л Л … 4 И И Л И Л Л … 5 И Л Л Л И Л … 6 И И И Л Л И … - -- -- -- -- -- -- --
![]() ,
,![]() .
Рассмотрим предикаты
.
Рассмотрим предикаты![]() ,
,![]() и высказывания
и высказывания![]() ,
,![]() .
Имеем
.
Имеем![]() .
Так как при каждом конкретном натуральном
значениих = а высказывание
.
Так как при каждом конкретном натуральном
значениих = а высказывание
![]() истинно,
истинно,![]() – И, т.е.
– И, т.е.![]() – И. Далее
– И. Далее![]() .
Так как прих =
2 высказывание
.
Так как прих =
2 высказывание
![]() ложно, то
ложно, то![]() – Л, т.е.
– Л, т.е.![]() – Л.
– Л.
Рассмотрим
![]() .
Так как приу
= 1 высказывание
.
Так как приу
= 1 высказывание![]() истинно, то
истинно, то![]() – И,
– И,![]() – И.
– И.
Наконец, выясним
истинностное значение каждого из
высказываний
![]() и
и![]() .
Имеем
.
Имеем![]()
![]() .
Введем
.
Введем![]() и возьмем произвольное натуральное
значениех
= а. Тогда
и возьмем произвольное натуральное
значениех
= а. Тогда
![]() является истинным высказыванием.
Действительно, еслиy
= b
, то
является истинным высказыванием.
Действительно, еслиy
= b
, то
![]() истинно, так как в случае ложной посылки
импликация истинна, а в случае истинной
посылки натуральное делимое всегда
больше половины натурального делителя.
Итак, предикат
истинно, так как в случае ложной посылки
импликация истинна, а в случае истинной
посылки натуральное делимое всегда
больше половины натурального делителя.
Итак, предикат![]() при каждом конкретном значениих
принимает значение И. Значит
при каждом конкретном значениих
принимает значение И. Значит
![]() – И. Далее из того, что
– И. Далее из того, что![]() – И, следует
– И, следует![]() – И.
– И.
Значит
![]() истинное высказывание.
истинное высказывание.
П р и м е р 25.
Перевести предложение на математический
зык, построить его отрицание и это
отрицание перевести на русский язык:
«Всякое натуральное число, обладающее
тем свойством, что оно представимо в
виде суммы двух натуральных чисел,
делящихся на 5, само делиться на 5». Имеем:
![]() ;
;
![]()
![]()
![]()
![]() .
.
В переводе последняя формула означает, что существует натуральное число х, представимое в виде суммы двух натуральных чисел, делящихся на 5, но само число х на 5 не делится.
П р и м е р 26. Дать определение ограниченной действительной функции, построить его отрицание, и это отрицание сформулировать по-русски.
Решение. Имеем:
действительная функция f
называется ограниченной, если найдется
действительное с
со свойством: при любом действительном
х
из того, что
![]() определено, следует
определено, следует![]() .
Значит,f
– ограниченна
.
Значит,f
– ограниченна![]() .
.
Поcтроенное отрицание ограниченности f записывается так:
f
– не ограничена![]() .
Итак, функцияf
не ограничена,
если при всяком действительном с
найдется действительное число х
из области определения f
такое, что
.
Итак, функцияf
не ограничена,
если при всяком действительном с
найдется действительное число х
из области определения f
такое, что
![]() .
.
П р и м е р 27. Докажем,
что
![]() .
.
Решение.
При n=1
утверждение справедливо, так как
![]() .
Предположим, что оно верно приn=k,
т.е.
.
Предположим, что оно верно приn=k,
т.е.
![]() .
Докажем, что тогда оно верно и приn=k+1,
т.е.
.
Докажем, что тогда оно верно и приn=k+1,
т.е.
![]()
В самом деле
![]()
![]() Тем
самым доказана справедливость утверждения
для любого натурального числа n.
Тем
самым доказана справедливость утверждения
для любого натурального числа n.
П р и м е р
28. Докажем,
что
![]() при любом натуральномn.
при любом натуральномn.
Решение.
Если n=1,
то
![]() ,
но
,
но![]() .
Значит, приn=1
утверждение
.
Значит, приn=1
утверждение
![]() верно. Предположим, что оно верно приn=k,
т.е.
верно. Предположим, что оно верно приn=k,
т.е.
![]() .
Докажем, что тогда оно верно и приn=k+1.
В самом деле, имеем
.
Докажем, что тогда оно верно и приn=k+1.
В самом деле, имеем
![]()
![]() .
Каждое слагаемое делится на 64,
следовательно, и вся сумма делится на
64. Итак, утверждение
.
Каждое слагаемое делится на 64,
следовательно, и вся сумма делится на
64. Итак, утверждение
![]() верно при всех
верно при всех![]() .
.
П р и м е р 29. Докажем,
что если
![]() ,
то
,
то![]() .
.
Решение.
Выражение, содержащееся в левой части
неравенства, представляет собой сумму
дробей, знаменатели которых – натуральные
числа от 1 до 2n
– 1. При n=1
оно обращается в верное числовое
неравенство
![]() .
Предположим, что неравенство
.
Предположим, что неравенство![]() выполняется приn
= k,
т.е.
выполняется приn
= k,
т.е.
![]() .
.
Докажем, что тогда
неравенство
![]() справедливо и приn=k+1,
т.е.
справедливо и приn=k+1,
т.е.
![]() .
.
В самом деле
![]() ,
где
,
где![]() .
ВыражениеPk
представляет собой сумму 2k
дробей, каждая из которых больше, чем
.
ВыражениеPk
представляет собой сумму 2k
дробей, каждая из которых больше, чем
![]() .
Значит,
.
Значит,![]() .
.
Итак,
![]() .
Но тогда
.
Но тогда![]() ,
т.е.
,
т.е.![]() .
.
На основании
принципа математической индукции
заключаем, что неравенство
![]() справедливо для любого
справедливо для любого![]() .
.
