
- •Глава I. Элементы теории множеств
- •Вопросы для самопроверки
- •Разберите решения следующих примеров
- •Задачи для самостоятельного решения
- •Глава II. Алгебра высказываний
- •Вопросы для самопроверки
- •Разберите решение следующих примеров
- •Приложения алгебры высказываний
- •Задачи для самостоятельного решения
- •Глава III. Алгебра предикатов
- •Вопросы для самопроверки
- •Разберите решения следующих примеров
- •Задачи для самостоятельного решения
- •Глава IV. Бинарные отношения
- •Вопросы для самопроверки
- •Разберите решения следующих примеров
- •Задачи для самостоятельного решения
- •Глава V. Элементы комбинаторики
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
Приложения алгебры высказываний
Алгебра высказываний нашла применение в логико-математической практике. Во-первых, при анализе и синтезе контактных схем.
П р и м е р 15.Упростить релейно-контактную схему и определить условия ее работы.
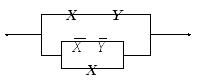
Решение. Запишем функцию проводимости этой схемы и преобразуем ее с помощью основных равносильностей алгебры высказываний.
![]()
![]()
![]()
По новой функции проводимости строим упрощенную схему:
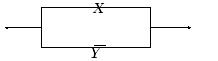
Из полученной
формулы, очевидно, что
![]() .
Это и есть условия работы данной схемы.
.
Это и есть условия работы данной схемы.
П р и м е р 16. Для комитета, состоящего из 4 человек сконструировать электрическую цепь так, чтобы лампочка зажигалась, если за данное предложение проголосовало меньшинство.
Решение.![]() Для
данных условий работы составим функцию
проводимости:
Для
данных условий работы составим функцию
проводимости:
![]()
![]()
Схема будет такой:
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()




![]()
![]()
![]()
![]()


![]()
![]()
![]()
![]()


![]()
![]()
![]()
![]()
![]()
Во-вторых, в
математике часто приходится формулировать
утверждения, которые являются отрицаниями
других утверждений, Обычно трудности
вызывают формулировки отрицаний сложных
предложений, в которых присутствует
импликация. Процесс нахождения удобной
формулировки отрицания некоторого
предложения в алгебре высказываний
получил название построения отрицания.
Чаще всего для формулы
![]() ,
имеющей в записи импликации, построить
отрицание означает следующее: для
формулы
,
имеющей в записи импликации, построить
отрицание означает следующее: для
формулы![]() найти равносильную и по возможности
простую формулу
найти равносильную и по возможности
простую формулу![]() ,
в которой нет импликаций, а знаки
отрицания (если они есть) относятся
только к атомам. При построении отрицаний
большую роль играют законы де Моргана,
закон исключения импликации, закон
двойного отрицания.
,
в которой нет импликаций, а знаки
отрицания (если они есть) относятся
только к атомам. При построении отрицаний
большую роль играют законы де Моргана,
закон исключения импликации, закон
двойного отрицания.
П р и м е р 17. Перевести предложение «Если я устал или голоден, то не могу заниматься» на логический язык, построить его отрицание и сформулировать это отрицание по-русски.
Введем атомы:
![]() «Я устал»,
«Я устал»,![]() «Я голоден»; наконец,
«Я голоден»; наконец,![]() «Я могу заниматься». Тогда заданное
предложение запишется формулой
«Я могу заниматься». Тогда заданное
предложение запишется формулой![]() .
Далее
.
Далее![]()
Значит, отрицание предложения формулируется так: «Я либо устал, либо голоден, но могу заниматься».
В-третьих, аппарат алгебры высказываний позволяет выяснять правильность выводов из некоторого списка положений.
П р и м е р 18. Проанализировать правильность вывода в рассуждении: «Если Коля дома, то у него горит свет и отрыто окно. Свет у Коли не горит. Значит, его нет дома».
Введем атомы:
![]() «Коля дома»,
«Коля дома»,![]() «У Коли горит свет»;
«У Коли горит свет»;![]() «У Коли открыто окно». Тогда заданное
рассуждение запишется в виде
«У Коли открыто окно». Тогда заданное
рассуждение запишется в виде![]() .
Чтобы убедиться в его правильности,
достаточно показать, что формула
.
Чтобы убедиться в его правильности,
достаточно показать, что формула![]() является тождественно истинной. Имеем:
является тождественно истинной. Имеем:![]()
![]()
![]()
![]() .
.
И, наконец, с помощью алгебры высказываний можно решать различные логические задачи.
Обобщённый приём решения логических задач методом алгебры высказываний:
1.Выделяем и обозначаем все участвующие в задаче простые высказывания;
2. Строим из них содержащиеся в условии задачи сложные высказывания;
3.Рассматриваем конъюнкцию построенных посылок, она истинна по условию;
4,Преобразуем эту конъюнкцию с помощью логических равенств к более простому виду, удобному для получения требуемой в задаче информации;
5. Извлекаем эту информацию (ответы на вопросы задачи).
Воспользуемся данным приёмом при решении логической задачи.
П р и м е р 19. Согласно инструкции капитан должен находиться на судне всегда, за исключением случаев, когда с судна выгружают груз; если же груз не выгружают, то рулевой никогда не отсутствует, если не отсутствует капитан. В каких случаях рулевой обязан присутствовать на судне?
Решение.
1. Введём обозначения, соответствующие
простым высказываниям:
![]() «Капитан присутствует на судне»;
«Капитан присутствует на судне»;![]() «С судна выгружают груз»;
«С судна выгружают груз»;![]() «Рулевой
присутствует на судне».
«Рулевой
присутствует на судне».
2. В инструкции
могут быть выделены одно простое и два
сложных высказывания:
![]() .
.
3.
![]() .
.
4. Упростим данную
конъюнкцию:
![]()
![]()
![]() .
.
5. Ответ: Если с судна не выгружают груз, то рулевой обязан присутствовать вместе с капитаном.
П р и м е р 20. Три девушки: Аля, Валя и Катя ходили в театр. Одна из них была в красном платье, другая – в белом, третья – в синем. На вопрос, какое на каждой из девушек было платье, они дали ответ: Аля была в красном, Катя – не в синем, Валя – не в красном. В этом ответе из трех частей одна верна, две – не верны. В каком платье была каждая из девушек?
Решение. Введем обозначения:
![]() –Аля в красном
платье;
–Аля в красном
платье;
![]() –Катя в синем
платье;
–Катя в синем
платье;
![]() –Валя в красном
платье, и тогда ответ, который дали
девушки, можно записать в виде конъюнкции
–Валя в красном
платье, и тогда ответ, который дали
девушки, можно записать в виде конъюнкции
![]() .
Так как по условию в этом ответе из трех
частей одна верна, а две не верны, то
истинна следующая дизъюнкция:
.
Так как по условию в этом ответе из трех
частей одна верна, а две не верны, то
истинна следующая дизъюнкция:
![]() .
.
Упростив эту формулу, получаем
![]() .
.
Поскольку первая
и третья конъюнкции ложны, то истинна
![]() ,
то есть: Валя в красном платье, Катя в
белом платье, Аля в синем платье.
,
то есть: Валя в красном платье, Катя в
белом платье, Аля в синем платье.
