Глава I. Элементы теории множеств

Л.М.Мартынов. Вводный курс математики, стр.9-19

Вопросы для самопроверки

1. Какие термины для обозначения многого как единого целого имеются в русском языке? Множество – это совокупность объектов (предметов или понятий), которая мыслится как единое целое. Объекты, входящие в эту совокупность, называются элементами множества.

2. Верна ли запись: 1 да, 2 нет

3. Принадлежит ли число 9 множеству ?да

4. Верно ли включение ?нет

5. Какое из множеств (1;4) и [1;4] включается в другое? 1 включает 2

6. Можно ли записать да

7. Какая из записей верна: ?оба

8. Сколько элементов содержат множества: ?3

9. В каком случае

10. Что означает запись х не принадлежит пересечению а и в

11. Когда выполняется равенство если а=в симметрическая разность

12. Что означает запись х не принадлежит разности а и в

13. Когда возможно равенство

14. Как проще записать множество

15. Если R–универсальное множество, то каково дополнение множества

16. В каком случае возможно равенство

Разберите решения следующих примеров

П р и м е р 1. Задайте перечислением следующие множества:

a) всех целых делителей числа 16;

б)

в) .

Решение. a) Так как натуральными делителями числа 16 являются числа 1,2,4,8,16, то искомым множеством будет {–16, –8, –4, –2, –1, 1, 2, 4, 8, 16}.

б) Так как целыми делителями числа 24 являются числа , то, выбрав из них только четные, мы получим множество. Значит искомое множество.

в) Натуральных чисел, меньших 12, и при этом кратных 3 всего три: 3, 6, 9. Следовательно, искомое множество

П р и м е р 2. Принадлежит или включается множество А во множество В, если

a);

б)

Решение. a) Множествоявляется подмножеством множестватак как каждый элемент первого множества принадлежит второму множеству:. Следовательно. Но в то же время множествоявляются элементом множестваи поэтому.

б) Множество является подмножеством множестват.к.. Значит,.

П р и м е р 3. Найдите множество А^* всех подмножеств множества:

a) ;

б) ;

в) .

Решение.

a) ;

б) ;

в) .

П р и м е р 4. Справедливы ли утверждения:

a) ;

б) ;

в)

Решение. a) Множества иравны, так как объекты, входящие в состав этих множеств, то есть элементы, одинаковы и отличается только порядок записи этих элементов.

б) Множества иравны, так как каждый элемент первого множества принадлежит второму множеству и, наоборот.

в) Так как элемент второго множеств не принадлежит первому множеству, то множестваине равны.

П р и м е р 5. Выяснить, какое множество является подмножеством другого:

а) и (0;3);

б) и (2;5];

в) и.

Решение. a) Так как =, а (0;3) – множество всех действительных, удовлетворяющих неравенству, то, то есть первое множество является подмножеством второго.

б) Ни одно из этих множеств не является подмножеством другого, поскольку в каждом из них есть элементы, не содержащиеся в другом, например, 2 и 5.

в) Множество является подмножествомпотому, что приk=1 , а приk= –3 .

П р и м е р 6. Пусть ,. Выяснить какие из чисел 1, 2, 3, 4, 5 принадлежат множествам.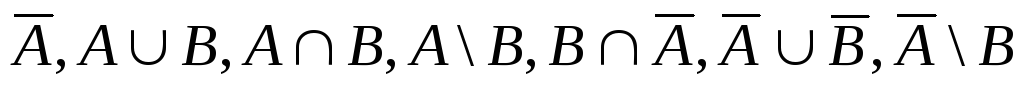

Решение. Множества иможно задать перечислением элементов:,. Поэтому легко найти их объединение, пересечение, разностьи ответить на вопрос задачи,,.

–дополнение множества , а значит,,. Множествуни одно из чисел 1,2,3,4,5 не принадлежит.

П р и м е р 7. Доказать закон де Моргана .

Решение. Доказательство разбивается на две части.

1) Докажем, что если , то.

Пусть . По определению дополнения. Следовательно,или. Но тогдаили, значит.

2) Докажем, что если , то.

Пусть . Тогда, по определению объединенияили. По определению дополненияили. Следовательно,, то есть.

П р и м е р 8. Упростить запись множества, используя основные законы алгебры множеств:

a) ;

б) .

Решение. Используя равенства 1-12 (стр.15 учебного пособия Л.М.Мартынова), получим следующие преобразования:

a)

б)

П р и м е р 9. Доказать включение и проиллюстрировать его диаграммами Эйлера-Венна.

Решение. 1-й способ (универсальным методом).

Для доказательства включения необходимо показать, что любой элемент множества принадлежит множеству. По определению разностиимееми. Но если, то тем более, то есть, что и требовалось доказать.

2-й способ (с использование основных законов алгебры множеств). Преобразуем левую часть включения: . Теперь используем диаграммы Эйлера-Венна дли иллюстрации этого включения.

Левая часть включения изображается диаграммой на рис.1.

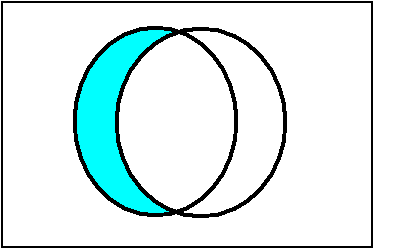
Рис. 1

Правая часть включения – диаграммой на рис. 2.

Рис. 2

П р и м е р 10. Доказать равенство и проиллюстрировать его диаграммой Эйлера-Венна.

Решение. Воспользуемся основными законами алгебры множеств:

.

Для иллюстрации доказанного равенства нарисуем последовательно несколько диаграмм, изображающих левую часть равенства (рис.3-8), а затем правую часть равенства (рис.9-11).

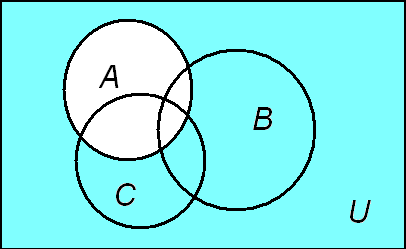
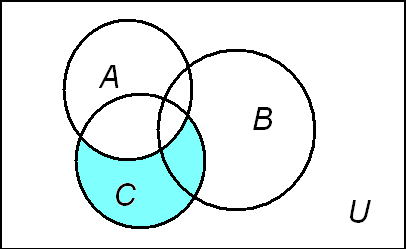
Рис. 3 Рис. 4

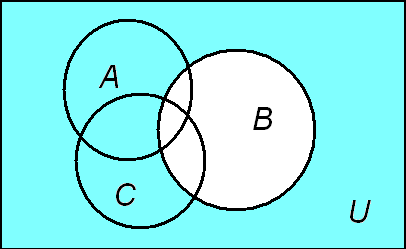
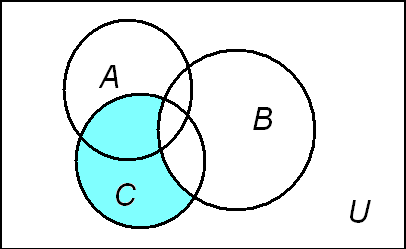
Рис. 5 Рис. 6

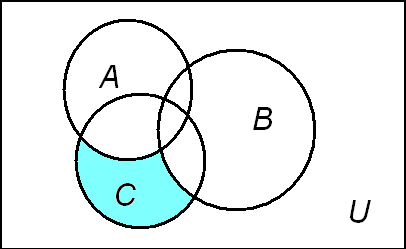
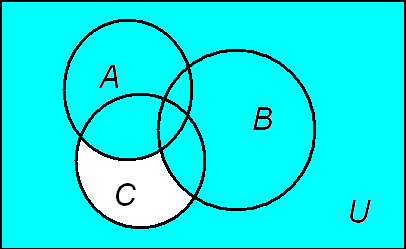
Рис. 7 Рис. 8

Несколько таких рисунков можно объединить в один, используя для штриховки цветные карандаши.

Правую часть равенства необходимо изобразить на отдельном рисунке, не меняя взаимного расположения множеств А, В, С.

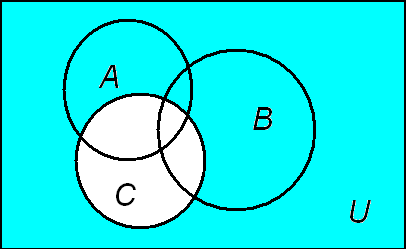
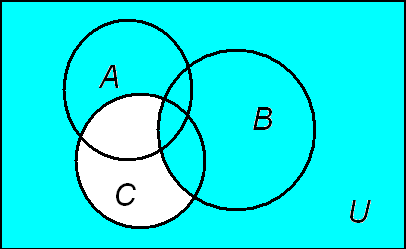
Рис. 9 Рис. 10

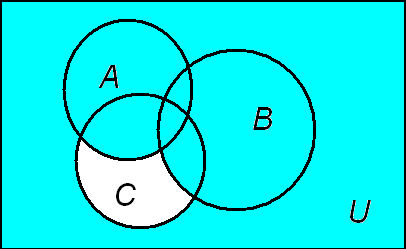
Рис. 11

Сравнивая рисунки 8 и 11, мы видим, что они одинаковы. Это и является иллюстрацией доказанного равенства (но не доказательством!).

П р и м е р 11. Пусть А – множество решений уравнения В – множество решений уравнения . Выразите черезА и В множество решений уравнений:

а) ;

б) и системы в)

Ответ: а) ; б); в).

П р и м е р 12. Решить систему неравенств:

Решение. Множество решений первого неравенства . Решив второе неравенство методом интервалов, получим множество (–1;6). Чтобы получить Решение системы неравенств, найдём пересечение двух множеств. Геометрически это можно изобразить так:

Рис. 12

Пересечением множеств является множество точек, на котором штриховки накладываются друг на друга.

П р и м е р 13. Решить систему неравенств:

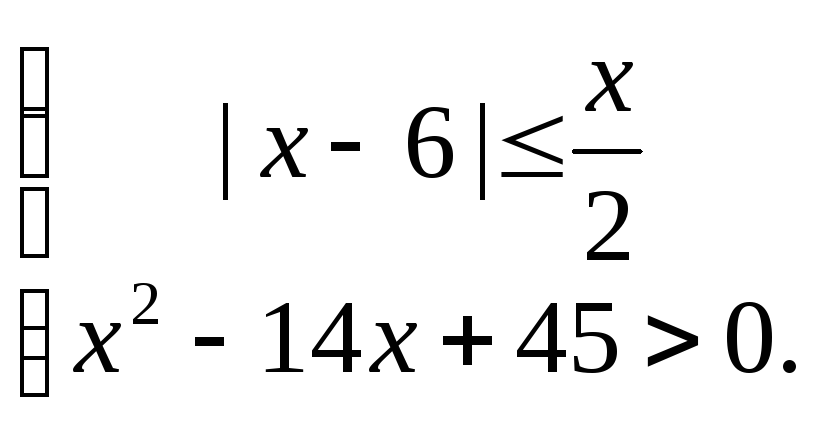
Решение. Раскрывая модуль в первом неравенстве системы, получим два случая. Учитывая второе неравенство, приходим к совокупности двух систем:

1) 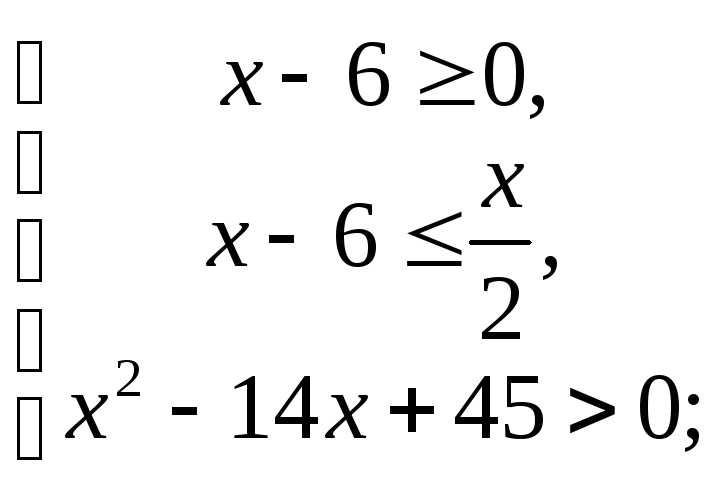или 2)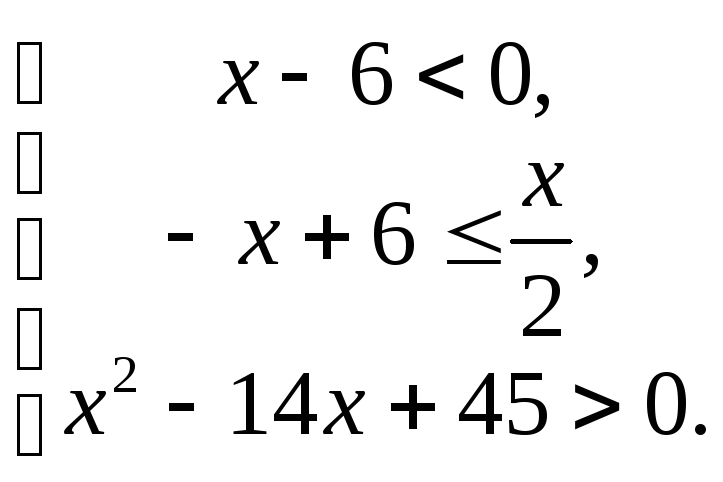

Множество решений первой системы есть пересечение трех множеств: . Найдем пересечение первого и второго множества. Используя дистрибутивный закон пересечения относительно объединения, будем иметь:.

Теперь решим вторую систему из совокупности. Проводя аналогичные рассуждения, как и в первом случае, получим три множества: и. Найдем их пересечение:.

Множество решений исходной системы является объединением множестви, то есть

П р и м е р 14. Из 20 человек двое изучали только английский язык, трое – только немецкий, шестеро – только французский. Никто не изучал трёх языков. Один изучал немецкий и английский, трое – французский и английский. Сколько человек изучало французский и немецкий языки?

Рис. 13

Решение. Обозначим через А множество учеников, изучавших английский язык, через В – немецкий язык, через С – французский язык.

По условию множество содержит один элемент, множествосодержит 3 элемента,(никто не изучал сразу три языка). Требуется определить количество элементов в пересечении(рис. 13).

Объединение множеств содержит 20 элементов. Из диаграммы видно, что множестводолжно содержать 20–1–2–3–6–3=5 элементов.

Ответ: французский и немецкий языки изучали 5 человек.