
- •Н.А. Курганова
- •Тема 1. Постановка задачи линейного программирования. Геометрический метод решения задач линейного программирования. Основные понятия, теоремы, следствия. 6
- •Тема 2. Симплекс-метод. 45
- •Введение
- •Тема 1. Постановка задачи линейного программирования. Геометрический метод решения задач линейного программирования. Основные понятия, теоремы, следствия.
- •1.1. Постановка задачи линейного программирования
- •Виды задач лп:
- •Постановка задачи линейного программирования (лп).
- •1.2. Геометрический метод решения задач лп
- •Варианты одр:
- •Теоретические вопросы
- •Лабораторная работа №1. Геометрическое решение задачи лп при помощи математического пакета MathCad
- •I. Оформление исходных данных.
- •II. Определение области допустимых решений
- •III. Построение линии уровня
- •IV. Нахождение оптимального плана и оптимального значения целевой функции
- •Лабораторная работа №2. Геометрическое решение задачи лп при помощи математического пакета Maple
- •I. Оформление заголовка.
- •II. Определение области допустимых решений.
- •III. Построение линии уровня.
- •IV. Нахождение оптимального плана и оптимального значения целевой функции
- •Задания для самостоятельной работы
- •Задачи о составлении плана производства
- •Задачи о пищевом рационе
- •Лабораторная работа №3. Решение оптимизационных задач в системах MathCad, Maple, Excel, в специализированном пакете SimplexWin.
- •I. Оформление исходных данных.
- •II. Нахождение оптимального плана и оптимального значения целевой функции.
- •Решение оптимизационных задач в специализированном пакете SimplexWin. Http://www.Simplexwin.Narod.Ru/
- •I. Оформление исходных данных.
- •II. Нахождение оптимального плана и оптимального значения целевой функции.
- •I. Оформление исходных данных.
- •II. Нахождение оптимального плана и оптимального значения целевой функции.
- •Задания для самостоятельной работы
- •Тема 2. Симплекс-метод.
- •Для реализации симплекс-метода необходимо освоить
- •3 Основных момента [7]:
- •2.1. Табличный симплекс-метод (в чистом виде)
- •2.2. Табличный симплекс метод. Метод искусственного базиса (м-метод)
- •Общий алгоритм решения задачи м-методом.
- •Теоретические вопросы
- •Лабораторная работа №4. Реализация пошагового алгоритма решения задачи линейного программирования табличным симплекс-методом средствами Excel при выполнении всех условий
- •I. Проверка выполнения условий, необходимых для решения задачи табличным симплекс-методом в чистом виде.
- •II. Оформление исходных данных.
- •III. Нахождение оптимального плана и оптимального значения целевой функции.
- •Лабораторная работа №5. Реализация пошагового алгоритма решения задачи линейного программирование методом искусственного базиса (м-методом) средствами Excel
- •I. Проверка выполнения условий, необходимых для решения задачи табличным симплекс-методом.
- •II. Оформление исходных данных.
- •III. Нахождение оптимального плана и оптимального значения целевой функции.
- •Задания для самостоятельной работы
- •Приложение 1
- •Приложение 2
- •Библиографический список
2.2. Табличный симплекс метод. Метод искусственного базиса (м-метод)
Среди задач линейного программирования встречаются такие задачи, когда не выполняется условие наличия базисной переменной в каждом из ограничений, то есть не выполняется условие 3 для решения задачи табличным симплекс-методом в чистом виде. В таком случае при решении задач линейного программирования необходимо использовать метод искусственного базиса (М-метод).
Общий алгоритм решения задачи м-методом.
Проверьте выполнение следующих условий:
-
правые части всех уравнений системы
неотрицательны (![]() );
);
-
задача каноническая, т.е. система
ограничений должна быть представлена
в виде уравнений, исходная функция
направлена на
![]() ;
;
Замечание. Возможные действия, если не выполняется условия 1 и 2 рассмотрены в пункте 2.1.
Таким образом, получите каноническую задачу, в которой все свободные члены положительны.
![]()

![]()
Найдите базисные переменные, если они есть, в исходных ограничениях.
Найдите ограничение или ограничения, в которых нет базисных переменных, и определитесь с количеством искусственных переменных.
Составьте расширенную задачу, добавив искусственные переменные к тем ограничениям, где нет базисных переменных.
Расширенная задача:
![]()
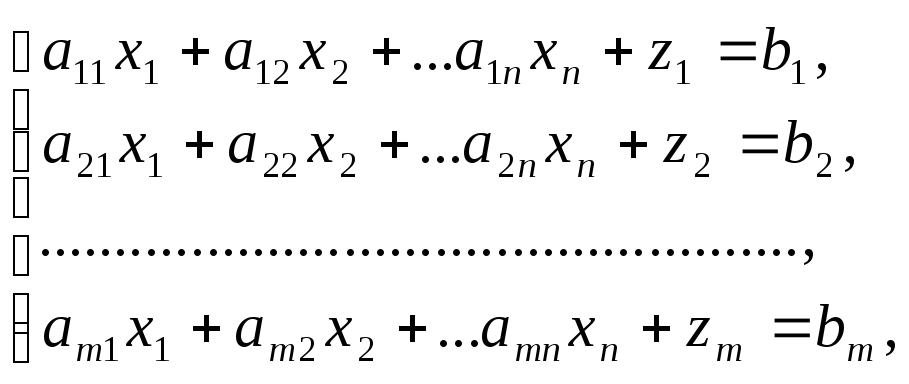
![]() ,
,![]() ,
,
где
![]() - некоторое достаточно большое число.
- некоторое достаточно большое число.
Замечание.
Базисные переменные
![]() называются искусственными.
называются искусственными.
Реализуйте выполнение условия 4, то есть выразите целевую функцию через переменные, не вошедшие в базис.
![]()
Заполните симплексную таблицу, добавив столбцы, отвечающие за искусственные переменные.
Включите в симплексную таблицу ниже индексной строки
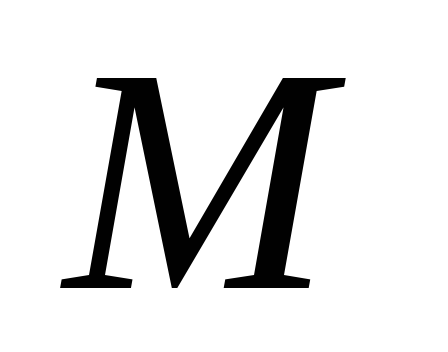 -строку.
-строку.Заполните
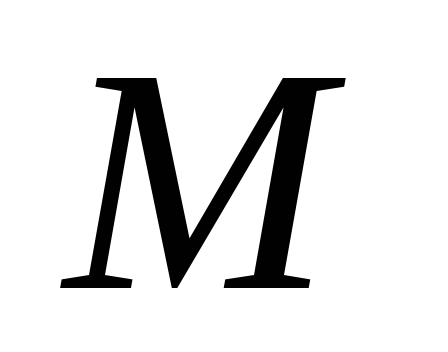 -строку
коэффициентами при переменных и
свободным членом по такому же правилу,
что и в табличном симплекс-методе в
чистом виде.
-строку
коэффициентами при переменных и
свободным членом по такому же правилу,
что и в табличном симплекс-методе в
чистом виде.Проверьте выполнение критериев остановки решения.
Если критерии остановки не выполняются, решайте задачу табличным симплекс-методом, опираясь на опорный план
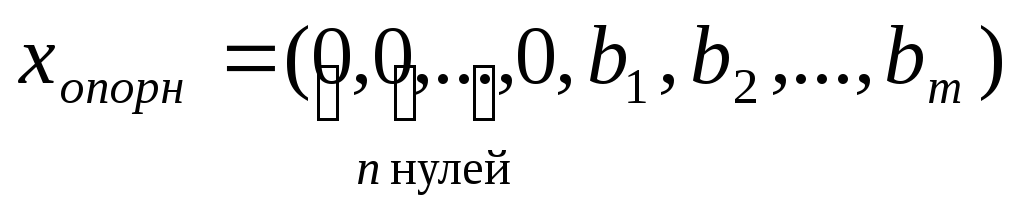 ,
одновременно ведите преобразования с
исходной функцией
,
одновременно ведите преобразования с
исходной функцией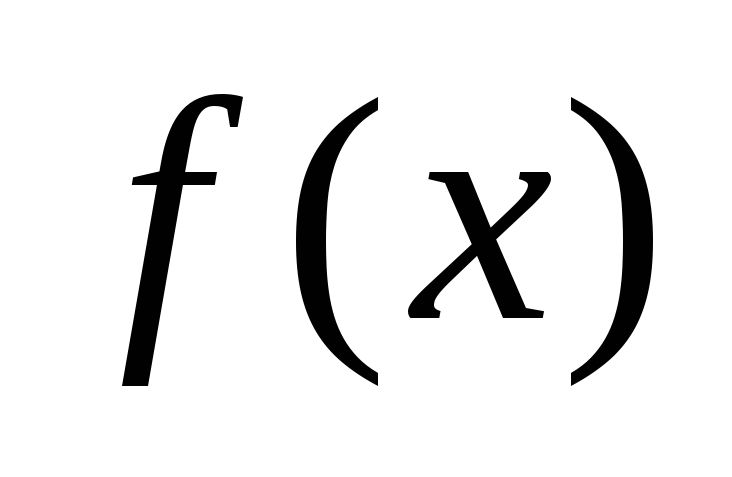 и с
и с -строкой,
до выполнения одного из критериев
остановки симплекс-метода.
-строкой,
до выполнения одного из критериев
остановки симплекс-метода.
Замечание. Для М-метода действуют все критерии остановки решения задачи линейного программирования табличным симплекс методом.
Теорема.
Если в оптимальном плане
![]() расширенной задачи значения всех
искусственных переменных
расширенной задачи значения всех
искусственных переменных![]() ,
то
,
то![]()
Перед выполнением лабораторных работ ответьте на теоретические вопросы.
Теоретические вопросы
Какие условия должны выполняться, для того чтобы можно было решать задачу ЛП табличным симплекс-методом в чистом виде?
Каким образом заполняется индексная строка симплексной таблицы?
Каков признак существования нового опорного плана, улучшающего целевую функцию?
Где записывается начальный опорный план при решении задачи линейного программирования табличным симплекс-методом?
Как выбирается ведущий столбец симплексной таблицы?
Что показывает выбранный ведущий столбец симплексной таблицы?
Как выбирается ведущая строка симплексной таблицы?
Что показывает выбранная ведущая строка симплексной таблицы?
Если
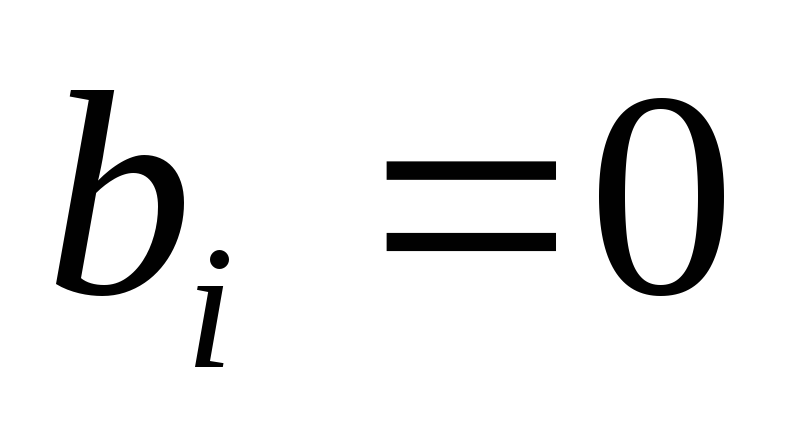 ,
,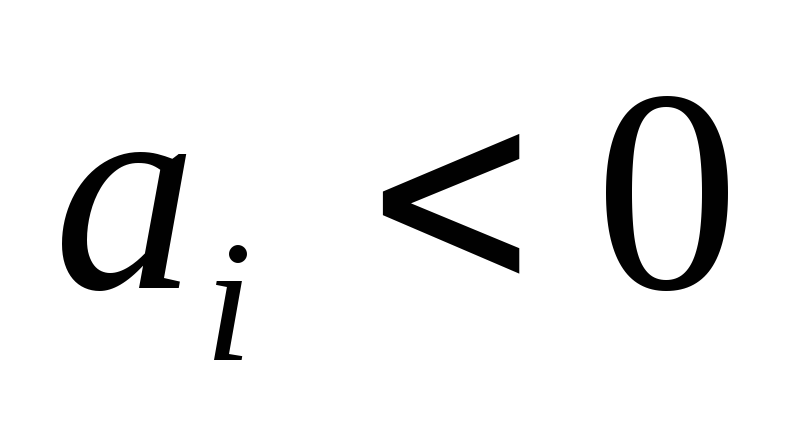 ,
то чему будет равен результат отношения
элемента столбца свободных членов к
соответствующему элементу ведущего
столбца?
,
то чему будет равен результат отношения
элемента столбца свободных членов к
соответствующему элементу ведущего
столбца?Если
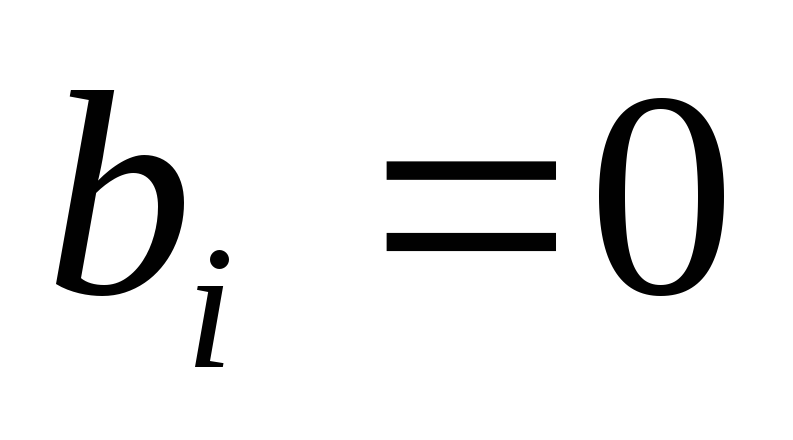 ,
, ,
то чему будет равен результат отношения
элемента столбца свободных членов к
соответствующему элементу ведущего
столбца?
,
то чему будет равен результат отношения
элемента столбца свободных членов к
соответствующему элементу ведущего
столбца?Если
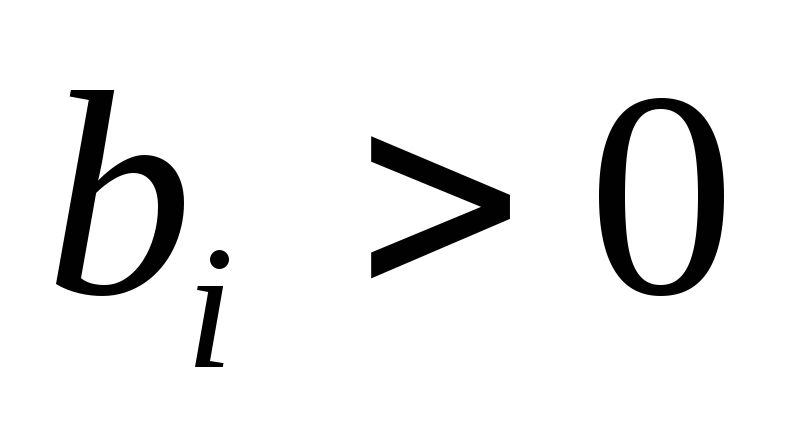 ,
,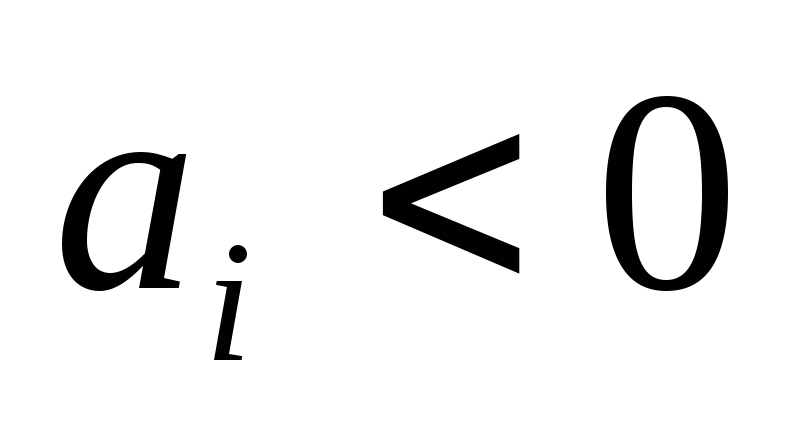 ,
то чему будет равен результат отношения
элемента столбца свободных членов к
соответствующему элементу ведущего
столбца?
,
то чему будет равен результат отношения
элемента столбца свободных членов к
соответствующему элементу ведущего
столбца?Если
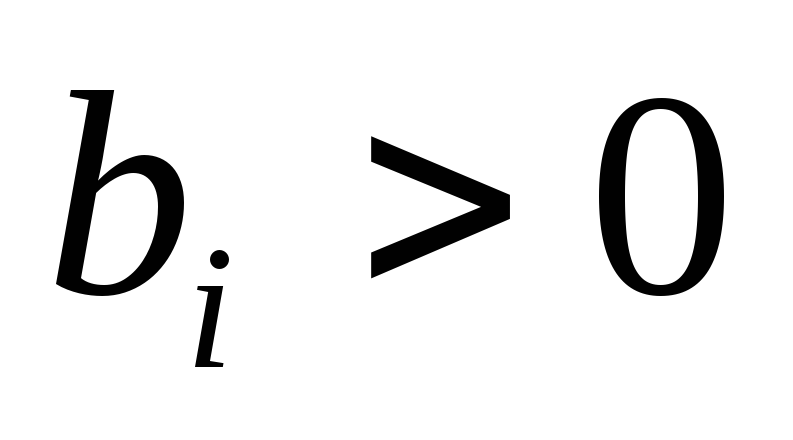 ,
,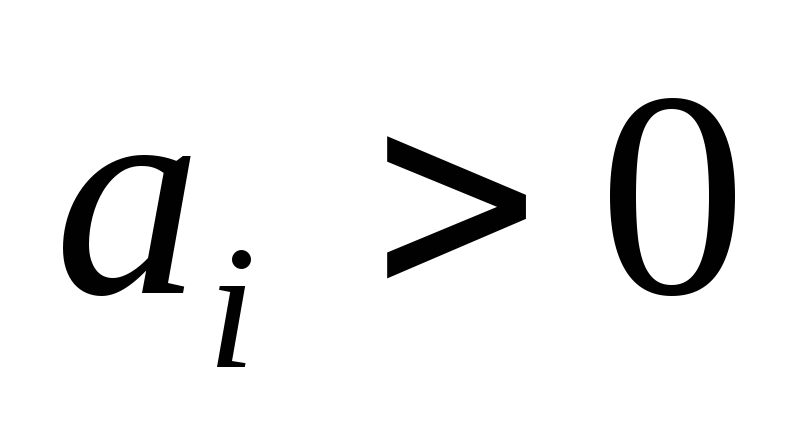 ,
то чему будет равен результат отношения
элемента столбца свободных членов к
соответствующему элементу ведущего
столбца?
,
то чему будет равен результат отношения
элемента столбца свободных членов к
соответствующему элементу ведущего
столбца?В чем смысл первого критерия остановки при решении задачи линейного программирования табличным симплекс методом в чистом виде?
В каком случае задача линейного программирования, решаемая табличным симплекс методом, не имеет оптимального решения, но имеет допустимые решения?
В каком случае задача линейного программирования, решаемая табличным симплекс методом, не имеет решений?
Как будет выглядеть вспомогательная функция для задачи линейного программирования, решаемой М-методом, если нам не хватает в исходной системе ограничений 2 базисные переменные?
Какое базисное решение называется реализуемым?
Какое базисное решение называется вырожденным?
