
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО
ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ДОНСКОЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра физики
ОПРЕДЕЛЕНИЕ ПОСТОЯННОЙ ПУАССОНА И ОЦЕНКА ЧИСЛА СТЕПЕНЕЙ СВОБОДЫ МОЛЕКУЛ ВОЗДУХА МЕТОДОМ
КЛЕМАНА-ДЕЗОРМА
Методические указания к лабораторной работе №5 по физике
(Раздел <<Молекулярная физика>>)
Ростов-на-Дону 2009
Составители: А.Б. Гордеева, В.Л. Литвищенко, В.С. Кунаков
УДК 530.1
ОПРЕДЕЛЕНИЕ ПОСТОЯННОЙ ПУАССОНА И ОЦЕНКА ЧИСЛА СТЕПЕНЕЙ СВОБОДЫ МОЛЕКУЛ ВОЗДУХА МЕТОДОМ КЛЕМАНА-ДЕЗОРМА: Метод. указания. – Ростов н/Д: Издательский центр ДГТУ, 2009.-12 с.
Указания содержат краткое описание рабочей установки и методику определения постоянной Пуассона.
Методические указания предназначены для студентов инженерных специальностей всех форм обучения, в программу учебного курса которых входит выполнение лабораторных работ по физике (раздел <<Молекулярная физика>>).
Печатается по решению методической комиссии факультета <<Нанотехнологии и композиционные материалы>>
Научный редактор проф., д. т. н. В.С. Кунаков
©Издательский центр ДГТУ, 2009
Лабораторная работа №5
ОПРЕДЕЛЕНИЕ ПОСТОЯННОЙ ПУАССОНА И ОЦЕНКА ЧИСЛА СТЕПЕНЕЙ СВОБОДЫ МОЛЕКУЛ ВОЗДУХА МЕТОДОМ
КЛЕМАНА-ДЕЗОРМА
Цель работы: Определение постоянной Пуассона и оценка числа степеней свободы молекул воздуха в результате проводимых в лабораторных условиях адиабатного и изохорного процессов.
Оборудование: экспериментальная установка, водяной манометр.
Теоретическая часть
Теплоемкость газа. Процессы, происходящие в газах.
Состояние
газа может быть охарактеризовано тремя
величинами – давлением
![]() ,
объемом
,
объемом![]() и
температурой
и
температурой![]() .
Уравнение, связывающее эти величины,
называется уравнением состояния
вещества. В случае идеального газа таким
уравнением является уравнение
Менделеева-Клапейрона, которое для
одного моля газа имеет вид:
.
Уравнение, связывающее эти величины,
называется уравнением состояния
вещества. В случае идеального газа таким
уравнением является уравнение
Менделеева-Клапейрона, которое для
одного моля газа имеет вид:
![]() (1)
(1)
где
![]() -
универсальная газовая постоянная.
-
универсальная газовая постоянная.
Молярная теплоемкость газа определяется количеством теплоты, которое необходимо сообщить 1 молю газа для нагревания его на 1 градус Кельвина.
Величина
молярной теплоемкости газов зависит
от условий нагревания. Для выяснения
такой зависимости воспользуемся
уравнением состояния (1) и первым началом
термодинамики, согласно которому
количество теплоты
![]() ,
переданное системе (газу), затрачивается
на увеличение её внутренней энергии
,
переданное системе (газу), затрачивается
на увеличение её внутренней энергии![]() и на работу
и на работу![]() ,
совершаемую системой (в данном случае
газом) против внешних сил:
,
совершаемую системой (в данном случае
газом) против внешних сил:
![]() (2)
(2)
Следовательно, по определению молярной теплоемкости:
![]() (3)
(3)
Из
выражения (3) следует, что теплоемкость
может иметь различные значения в
зависимости от способов нагревания
газа, так как одному и тому же значению
![]() могут соответствовать различные значения
могут соответствовать различные значения![]() и
и![]() .
Элементарная работа
.
Элементарная работа![]() ,
согласно [1], равна
,
согласно [1], равна![]() .
.
Из основного уравнения молекулярно-кинетической теории идеального газа известно, что среднее значение кинетической энергии поступательного движения одной молекулы [2]:
![]() ,
(4)
,
(4)
где
![]() -
постоянная Больцмана.
-
постоянная Больцмана.
Кинетическая
энергия многоатомных молекул зависит
от числа степеней свободы, которое
обозначается буквой
![]() .
Число степеней свободы – число независимых
координат полностью определяющих
положение системы (в данном случае
молекулы) в пространстве.
.
Число степеней свободы – число независимых
координат полностью определяющих
положение системы (в данном случае
молекулы) в пространстве.
Согласно теореме Больцмана на каждую степень свободы молекулы приходится одинаковое значение энергии. Средняя энергия произвольной молекулы идеального газа [2]:
![]() .
(5)
.
(5)
Так как в идеальном газе потенциальной энергией молекул пренебрегают, то внутренняя энергия одного моля идеального газа определяется только кинетической.
![]() ,
,
где
![]() - число Авогадро,
- число Авогадро,![]() -
универсальная газовая постоянная (
-
универсальная газовая постоянная (![]() ).
).
Дифференциал от внутренней энергии:
![]() (6)
(6)
Рассмотрим основные процессы, протекающие в идеальном газе при изменении температуры, когда масса газа остается неизменной и равна одному молю.
Изохорический процесс. Процесс называется изохорическим, если объем газа при изменении температуры остается неизменным, т.е.
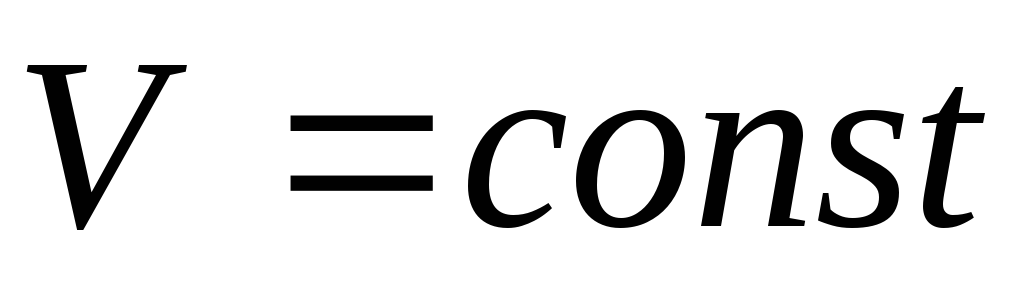 .
В этом случае
.
В этом случае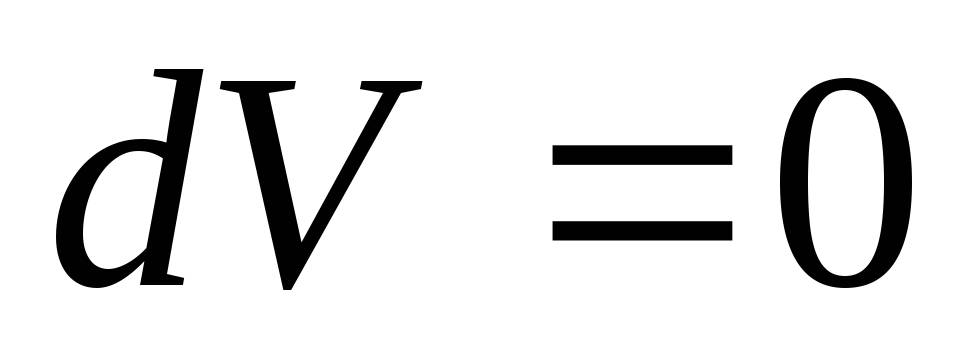 ,
работа газа также равна нулю (
,
работа газа также равна нулю (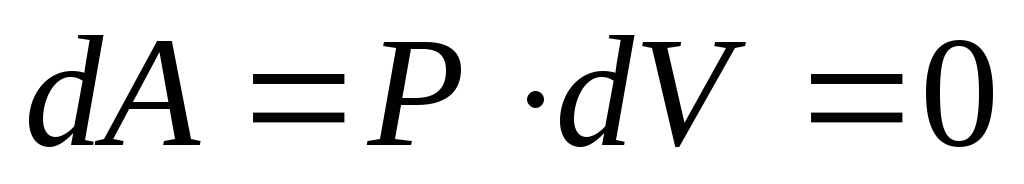 ),
а подводимая к газу теплота идет только
на увеличение его внутренней энергии.
В таком случае из уравнения (3)
),
а подводимая к газу теплота идет только
на увеличение его внутренней энергии.
В таком случае из уравнения (3)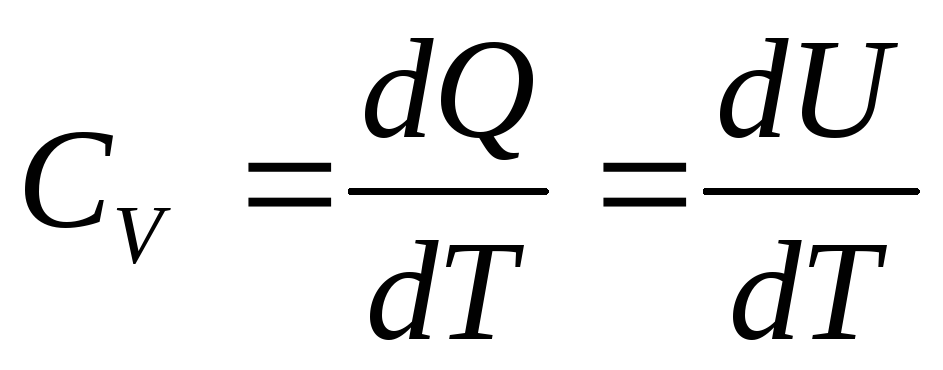 ,
а с учетом (6) молярная теплоемкость при
постоянном объеме:
,
а с учетом (6) молярная теплоемкость при
постоянном объеме:
![]() (7)
(7)
Изобарический процесс. Процесс, протекающий при постоянном давлении (
 ),
называется изобарическим. Молярную
теплоемкость при постоянном давлении
определим по формуле (3) с учетом, что
),
называется изобарическим. Молярную
теплоемкость при постоянном давлении
определим по формуле (3) с учетом, что
 :
:
![]() (8)
(8)
Возьмем дифференциал от правой и левой частей уравнения (1):
![]() ,
,
так
как
![]() ;(
;(![]() ),
получим:
),
получим:
![]() (9)
(9)
Подставив
в (8) вместо
![]() его значение из (9) и учитывая, что
его значение из (9) и учитывая, что![]() ,
получим значение молярной теплоемкости
при постоянном давлении:
,
получим значение молярной теплоемкости
при постоянном давлении:
![]() ,
или
,
или
![]() (10)
(10)
Следовательно,
![]() на величину универсальной газовой
постоянной.
на величину универсальной газовой
постоянной.
Изотермический процесс. Изотермическим называется процесс, протекающий при постоянной температуре (
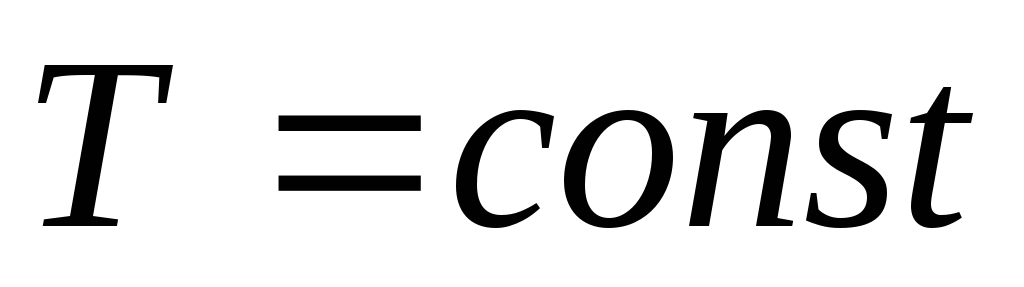 ,
,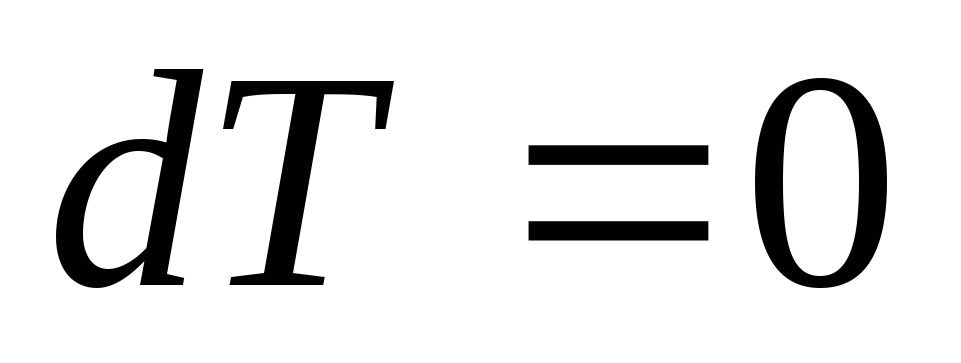 ,
а следовательно
,
а следовательно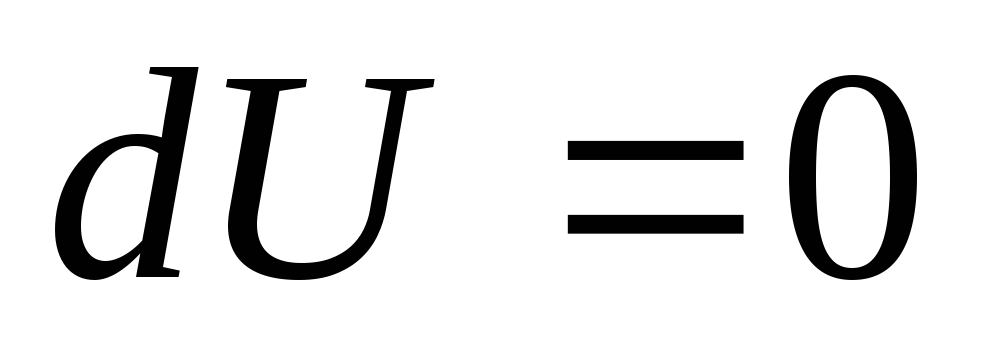 ).
В этом процессе внутренняя энергия не
меняется, а все подводимое тепло идет
на совершение работы (
).
В этом процессе внутренняя энергия не
меняется, а все подводимое тепло идет
на совершение работы ( ).
При изотермическом процессе при любых
изменениях давления или объема:
).
При изотермическом процессе при любых
изменениях давления или объема:
![]() (11)
(11)
Молярная теплоемкость при изотермическом процессе равна бесконечности.
Адиабатический процесс. Процесс, протекающий без теплообмена с окружающей средой, называется адиабатическим (
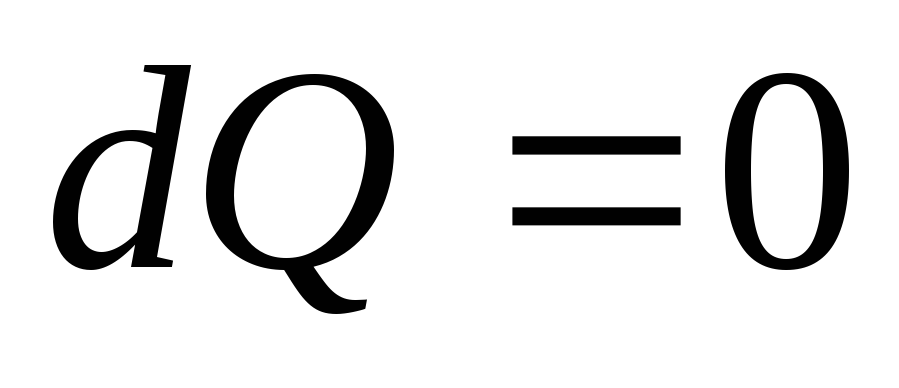 ).
).
Первое начало термодинамики (2) при таком процессе имеет вид:
![]() ,
,
Откуда
![]() ,
то есть при адиабатическом расширении
или сжатии, работа совершается газом
только за счет изменения внутренней
энергии газа.
,
то есть при адиабатическом расширении
или сжатии, работа совершается газом
только за счет изменения внутренней
энергии газа.
Адиабатический процесс описывается уравнением Пуассона, одна из форм которого имеет вид:
![]() ,
(12)
,
(12)
где
![]() - отношение, называемое постоянной
Пуассона [1].
- отношение, называемое постоянной
Пуассона [1].![]()
