
1-й сем-ДМ-слайды-ДГТУ / Графы, л.5-7 / Раскраски 1
.docРаскраски
Разнообразные задачи, возникающие при планировании производства , составлении графиков осмотра, хранении и транспортировке товаров могут быть представлены как
Задача о раскраске графа. Графы неориентированные и без петель(простые).
Граф G -
![]() -хрономический,
если его вершины могут быть раскрашены
с помощью
-хрономический,
если его вершины могут быть раскрашены
с помощью
![]() цветов
(красок) так, что не найдутся две смежных
вершин одного цвета. Наименьшее число
цветов
(красок) так, что не найдутся две смежных
вершин одного цвета. Наименьшее число
![]() такое,
что граф G -
такое,
что граф G -![]() -хрономический,
называется хрономическим число графа
-хрономический,
называется хрономическим число графа
G и обозначается
![]() (G).Задача
нахождений хрономического числа в графе
– задача о раскраски графа. Соответствующие
этому числу раскраски вершин разбивает
множество вершин графа на z
подмножества каждые из которых содержит
вершины одного цвета.
(G).Задача
нахождений хрономического числа в графе
– задача о раскраски графа. Соответствующие
этому числу раскраски вершин разбивает
множество вершин графа на z
подмножества каждые из которых содержит
вершины одного цвета.
Эти множества – независимые, т.к. в пределах 1 множества нет смежных двух вершин.
В общем случае хрономическое число графа нельзя найти , зная лишь числа вершин и рёбер графа. Недостаточно знать и степень каждой вершины, чтобы вычислить хрономическое число графа. Однако, можно получить верхнего и нижнего оценки для хрономического графа.
-
Если
 G)
равно мощности наибольшего множества
попарно несмежные вершины графа G
, то оно совпадает с мощностью наибольшего
множества вершин в G,
которые могут быть окрашены в один
цвет, и следовательно ,
G)
равно мощности наибольшего множества
попарно несмежные вершины графа G
, то оно совпадает с мощностью наибольшего
множества вершин в G,
которые могут быть окрашены в один
цвет, и следовательно ,
-
 (G)
(G)
 ,
где n –число вершин G,
а
,
где n –число вершин G,
а
 -
наименьшее целое число, не превосходящее
числа x.
-
наименьшее целое число, не превосходящее
числа x. -
Оценка Генера:
 (G)
(G)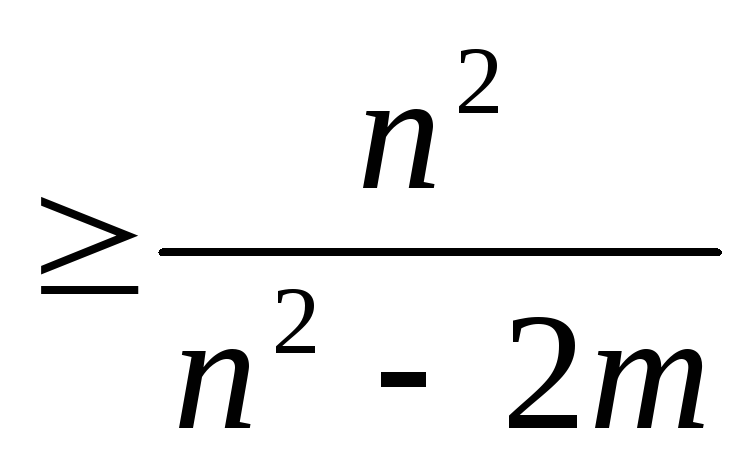 ,
где m- число рёбер графа.
,
где m- число рёбер графа.
Верхние оценки
-
 (G)
(G) -
Брукс
-
Брукс
Формулировка задачи о раскраски на языке Булева (0-1, математического)
Программирования.
Пусть
![]() -
матрица раскраски графа,
-
матрица раскраски графа,
![]()
1, если вершина
![]() окрашена
в цвет j,
окрашена
в цвет j,
0,в противном случае.
Если A=
![]() -
матрица смежности графа G
с диагональными элементами равными 0,
то следующие 2 условия гарантируют
допустимые раскраски вершин графа G:
-
матрица смежности графа G
с диагональными элементами равными 0,
то следующие 2 условия гарантируют
допустимые раскраски вершин графа G:
![]()
![]()
![]() ,
n (1)
,
n (1)
![]() ,
,
![]()
здесь q – верхняя оценка хрономического числа графа G. Условие (1) обеспечивает раскраску вершины в один и только один цвет. В(2) L- любое очень большое положительное число , больше чем n.
Если вершина
![]() окрашена в цвет j, то
окрашена в цвет j, то
![]() ,
то первый член в (2) равен 0.
,
то первый член в (2) равен 0.
Тогда и 2-й член =0, чтобы выполнялось
неравенство , т.к. числа
![]() и
и
![]() неотрицательны. Итак, (2) обеспечивает
раскраски, т.е., если вершина
неотрицательны. Итак, (2) обеспечивает
раскраски, т.е., если вершина
![]() окрашена в цвет
окрашена в цвет
j , то нет смежной с
![]() вершины того же цвета.
вершины того же цвета.
Если вершина
![]() окрашена в цвет, отличный от j,
то нет смежной с
окрашена в цвет, отличный от j,
то нет смежной с
![]() вершины того же цвета .Если вершина
вершины того же цвета .Если вершина
![]() окрашена в цвет отличный от j(
окрашена в цвет отличный от j(![]() )
, то первый член в (2) равен L
.Т.к. 2-й член в(2) не может достигнуть L(
его значение наибольшее равно n-1
, то какое-бы число вершин
)
, то первый член в (2) равен L
.Т.к. 2-й член в(2) не может достигнуть L(
его значение наибольшее равно n-1
, то какое-бы число вершин
![]() ,смежных
с вершиной
,смежных
с вершиной
![]() ,
ни было окрашено в цвет j
, неравенство (2) по-прежнему будет
выполнено.
,
ни было окрашено в цвет j
, неравенство (2) по-прежнему будет
выполнено.
Пусть теперь каждому цвету j
сопоставлен штраф
![]() выбранный тем , что
выбранный тем , что
![]() (штраф
(штраф
![]() =1)
–ф-и ( рекурентный).(3), где h
–верхние оценки для наибольшего числа
вершин в графе, которые могут быть
окрашены в 1 цвет, т.е. h –
произвольное число , больше , чем
=1)
–ф-и ( рекурентный).(3), где h
–верхние оценки для наибольшего числа
вершин в графе, которые могут быть
окрашены в 1 цвет, т.е. h –
произвольное число , больше , чем
![]() G)-
число независимости графа(максимальные
……… подмножества S
такого , что граф (S) вместе
несвязный –число независимости.
G)-
число независимости графа(максимальные
……… подмножества S
такого , что граф (S) вместе
несвязный –число независимости.
Любые 2 вершины в нём несмежны (![]() G)=
G)=
![]() , где Q – семейство всех
независимых множеств графа G
.)
, где Q – семейство всех
независимых множеств графа G
.)
Можно положить h=n!!!
Итак, имеем задачу минимизировать
Z=![]()
![]() min(4)
при ограничениях (1)(2).
min(4)
при ограничениях (1)(2).
Минимизация (4) обеспечивает выполнимость следующего условия :
Цвет j+1 будет ………. в раскраске вершин , если цвета от 1 до j достаточны для …….. раскраски.
Матрица
![]()
![]() определяет
оптимальную раскраску , а используемое
при этом число цветов равно хрономическому
числу графа.
определяет
оптимальную раскраску , а используемое
при этом число цветов равно хрономическому
числу графа.
Бернс вместо условия (2) предложил следующее:
![]() (5)
(5)
![]() -матрица
инцеденции. Условие(5)отражает тот факт,
что не более, чем 1 из 2-х концевых вершин
любого ребра может быть окрашено в цвет
j.
-матрица
инцеденции. Условие(5)отражает тот факт,
что не более, чем 1 из 2-х концевых вершин
любого ребра может быть окрашено в цвет
j.
В(5) требуется mq ограничений
В(2) nq ограничений, обычно m>n!!!
Приведём ряд теорем:
-
Ели наибольшее из степеней вершин графа G равен p, то он ( p+1)-раскашиваемый
-
a) Любой пленарный граф 5-………
б) любой пленарный граф, не содержит треугольников 3- раскрашенный (терема Грега).
с)граф G -2-x раскраски тогда и только тогда, когда он эйлеров.(теорема Кароля)
д) усиление a) еслиG
–простой связный граф , то он p-…….(р![]() ),где
р –наибольший из степеней вершин.
),где
р –наибольший из степеней вершин.
е) для n![]() вершина
4 – раскраски ……. и красок.
вершина
4 – раскраски ……. и красок.
Рёберная окраска
Граф G- рёберно к раскрашенный
, если его рёбра можно раскрасить К
окрасками таким образом, что некие 2
смежные ребра не окажутся 1 цвета. Если
граф К раскраски …….. , но не явится
(к-1)………, то К –хрономическое
число(……..)графа G.![]()
![]()
Ясно, что если наибольшее из степеней
вершин граф G равен р, то
![]() .
.
Алгоритм раскраски
Пусть множество вершин упорядочено и
![]() - вершина этого множества
- вершина этого множества
-
окрасить
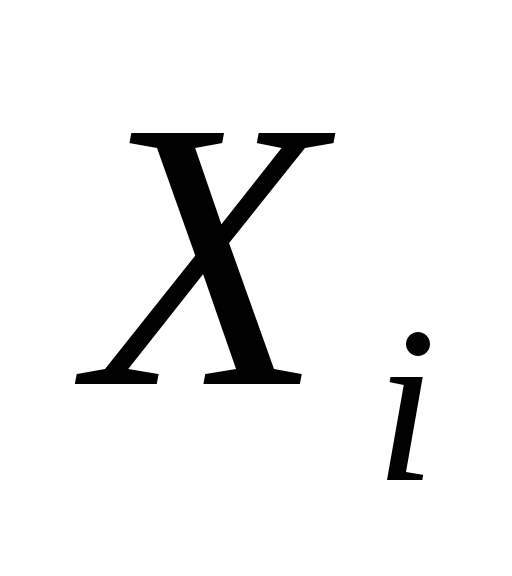 в
цвет 1
в
цвет 1 -
каждая из оставшихся вершин окрасить :
 в цвет с наименьшим возможным номером
( не использованный при окраски вершины,
смежной с
в цвет с наименьшим возможным номером
( не использованный при окраски вершины,
смежной с
 .
.
Связь с задачей раскраски
Пусть нужно выбрать время проведения лекций по различным предметам с учетом того , что студенты желают посещать и те и другие. Строим граф. Вершины его- лекции по различным предметам , а рёбра соединяют те пары лекций, которые не должны назначаться на 1 время. Если каждому предмету для лекции времени сопоставить некоторый цвет, то раскраски- правильное расписание.
Хроматические полиномы
Подсчитаем количество различных правильных К - раскрасок графа.
Если граф К –раскрашиваемый, то его можно раскрасить в К цветов более, чем одним способом. Две раскраски графа считаются различными, если хотя бы одной вершине графа присваиваются хроматический полином Р(G,К) имеет значение для каждого целого К, равное числу различных правильных К-раскрасок графа G.
Рассмотрим граф

Среди различных К цветов мы можем выбрать
любой для раскраски вершин а. Вершину
b можно раскрасить в один
из оставшихся К-1 цветов. Для каждой
раскраски вершины b
существует К-1 различных способов
раскраски вершины С. Итак, данный граф
можно раскрасить
![]() различными способами. Хрономатический
полином графа равен
различными способами. Хрономатический
полином графа равен
![]() .Повторяя
эти рассуждения , получим, что
хрономатический полином пути на n
вершинах равен
.Повторяя
эти рассуждения , получим, что
хрономатический полином пути на n
вершинах равен
![]()
Другим важным крайним случаем является
полный граф
![]() ,
имеющий n вершин. При ….
,
имеющий n вершин. При ….
n цветов вершину
![]() можно раскрасить в любой из них,
можно раскрасить в любой из них,
![]() -в
любой из оставшихся К-1 цветов, вершину
-в
любой из оставшихся К-1 цветов, вершину
![]() -в
любой из оставшихся К-2 цветов. Итак, Р
(
-в
любой из оставшихся К-2 цветов. Итак, Р
(![]() )=К(К-1),
и (К-n+1)
)=К(К-1),
и (К-n+1)
Выведем формулу для определения хроматического полинома графа G.
Теорема
Пусть U и V – несмежные вершины простого (без петель и циклов) графа G. Пусть е=(U,V)
Если G*e – простой граф полученный из графа G замыканием вершин U и V и заменой получившегося множества параллельным ребёр на одно ребро, а G+e – граф, полученный добавлением к графу G ребра е , то Р(G,К)=Р(G+е, К)+Р(G*e,К).
Док-во:
Любая К-раскраска графа G , в которой вершинам U и V присваиваются различные цвета , соответствует К-раскраска графа G+e , и наоборот .Аналогично, любая К-раскраска графа G , в которой U и V присвоен 1 цвет, соответствует К-раскраска графа G*e , и наоборот .
Следовательно, Р(G,К)=Р(G+е, К)+Р(G*e,К).
Можно сформулировать следствие
Если е=(U,V) –ребро простого графа G, то Р (G,К)=Р(G-е, К)+Р(G*e,К), где G-е получается из G удалением ребра е, а G*e определяется в теореме.
Если повторно применить формулу,
приведённую в теореме к графу G,
то процесс закончится полных графах,
например,![]() поэтому
Р(G,К)=
поэтому
Р(G,К)=![]()
![]()
С другой стороны, если использовать формулу следствия , то процесс закончится на пустых графах (без ребёр), поэтому хроматический полином- линейная комбинация хроматических полиномов пустых графов.
Хроматический полином Р (G,К)
графа на n вершинах имеет
степень n с главным числом
![]() и const.=0. Кроме того, все
коэффициенты целые и чередуются по
знаку.
и const.=0. Кроме того, все
коэффициенты целые и чередуются по
знаку.
Док-во:
Проведём индукцией по числу рёбер
m.Очевидно, что теорема
справедлива для m=0, т.к.
хроматический полином пустого графа
на n вершинах равен
![]() .Допустим,
что теорема верна для всех графов,
имеющих менее m рёбер ,
рассмотрим граф G на n
вершинах с m рёбрами. Пусть
е –ребро графа
G, тогда G-е
– граф на n вершинах
с m-1 рёбрами, а G*e
–граф на n-1 вершинах
с m-1 или менее рёбрами из
индуктивного предположения следует,
что существует такие неотрицательные
целые коэффициенты
.Допустим,
что теорема верна для всех графов,
имеющих менее m рёбер ,
рассмотрим граф G на n
вершинах с m рёбрами. Пусть
е –ребро графа
G, тогда G-е
– граф на n вершинах
с m-1 рёбрами, а G*e
–граф на n-1 вершинах
с m-1 или менее рёбрами из
индуктивного предположения следует,
что существует такие неотрицательные
целые коэффициенты
![]() и
и
![]() ,что
,что
Р(G-e,К)=![]() и
и
![]() .
Согласно следствию Р(G,К)=
.
Согласно следствию Р(G,К)=
= Р(G-e,К)-
Р(G*e,К)=![]() Таким образом, граф G также
удовлетворяет теореме.
Таким образом, граф G также
удовлетворяет теореме.
Пример 1
 =
=

+
 =
=

+

+


Р(G)=К(К-1)(К-2)(К-3) К(К-1)(К-2) К(К-1)(К-2) К(К-1)
К(К-1)(К-2)(К-3)+2К(К-1)(К-2)+К(К-1)=К(К-1)((К-2)(К-3)+2(К-2)+1)=К(К-1)![]() ;
Р(0)= Р(1)=0; P(2)=2*1
;
Р(0)= Р(1)=0; P(2)=2*1![]() 0,
(хроматический)
0,
(хроматический)
2-раскрашеный граф!
Пример 2
 =
=

 -
-

=
 -
-



-

 +
+

Р(G,K)=![]()
P(0)=P(1)=0
P(2)=2![]() 0,граф
2-раскрашиваемый
0,граф
2-раскрашиваемый
Пример 3
 =
=
 +
+
 =
=
 +
+

+
 +
+
 =
=

+
 +
+
 +
+ +
+

+
 =
=
 +3
+3
 +2
+2

=К(К-1)(К-2)(К-3)(К-4)+3К(К-1)(К-2)(К-3)+2К(К-1)(К-2)=К(К-1)(К-2)((К-3)(К-4)+3(К-3)+2)=К(К-1)(К-2)(![]() =
=![]() ;
;
при К=0,1,2, PG(K)=0
, при К=3: PG(K)![]() ,G-3-х
–хроматический граф.
,G-3-х
–хроматический граф.
Пример 4
G:

=G1
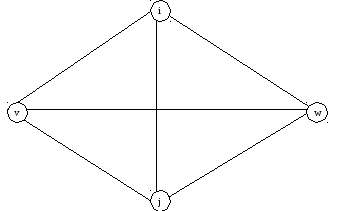 +G2
+G2

Тогда,
![]() =К
(К-1)(К-2)(К-3)+К (К-1)(К-2)=К (К-1)(К-2)(К-3+1)=К
(К-1)(К-2)
=К
(К-1)(К-2)(К-3)+К (К-1)(К-2)=К (К-1)(К-2)(К-3+1)=К
(К-1)(К-2)![]()
При К=0,1,2
![]() =0,
при К=3
=0,
при К=3
![]() =3*2*1=6
-граф 3- расрашеный
=3*2*1=6
-граф 3- расрашеный
Алгоритмы и программы.
А. Точный алгоритм раскрашивания
Имеем рекурсивную процедуру Р:
-
Выбрать в графе G некоторое максимальное независимое множество вершин S.
-
Покрасить вершины S в очередной цвет
-
Применить процедуру Р к графу GS
Выход: раскраски заданы массивом С![]() номера
цветов, при……….. вершинам
номера
цветов, при……….. вершинам
If V= ф then
Return (раскраска закончена)
End if
S: Select max
(G)![]() S-максимальное
независимое множество
S-максимальное
независимое множество![]()
C![]() :
=i
:
=i
![]() раскрашиваемые
вершины множества S в цвет
i
раскрашиваемые
вершины множества S в цвет
i![]()
P (G-S,
i+1)
![]() рекурсивный
вызов
рекурсивный
вызов![]()
Теорема
Если граф G К-раскрашенный, то существует такие последовательности выбора множества S на шаге 1 процедуры Р, что применение процедуры Р к графу G построит не более, чем К –раскраску графа G.
В.Приближённый алгоритм последовательного раскрашивания
Алгоритм А имеет переборный характер. Имеет смысл использовать приближённый алгоритм, ……………..эффективен.
Алгоритм последовательного приближения
Вход: граф G.
Выход: раскраска графа-массив С: ……..![]() of 1….P
of 1….P
For
![]() do
do
C![]() все
не раскрашены
все
не раскрашены![]()
End for
For
![]() do
do
A: =![]()
![]() все
цвета
все
цвета![]()
For
![]()
A:=A\
![]()
![]() занятые
для V цвета
занятые
для V цвета
![]()
End for
C![]() =
min A
=
min A
![]() минимально
свободный цвет
минимально
свободный цвет
![]()
End for
Замечание. Таким образом, красить вершины необходимо , выбирая среди допустимых цветов минимальный.
Обоснование. В основном цикле раскрашивания получаются все вершины, и каждая из них получает допустимую раскраску таким образом процедура строит допустимую раскраску.
С.Улучшенный алгоритм последовательной раскраски.
Алгоритм строит допустимую раскраску, применяя …………: начинать раскраску следует с вершин наибольшей степени, поскольку , если их раскрашивать в конце процесса, то более вероятно, что для них не найдётся свободного цвета и придется задействовать ещё 1 цвет.
Вход: граф G
Выход: раскраска графа –массив С:
……..![]() of 1….P
of 1….P
Sort (V) (упорядочить вершины по возрастанию степени)
С:=1( первый цвет)
For
![]() do
do
C![]() все
не раскрашены
все
не раскрашены![]()
End for
White V![]() do
do
For
![]() do
do
For
![]()
If C(U)= C then
Next for V (вершину V нельзя окрасить в цвет С)
End if
End for
C![]() ……
вершину V в цвет С
……
вершину V в цвет С![]()
V: =
![]() (удалям её из раскрашивания)
(удалям её из раскрашивания)
С: = С+1 (следующий цвет)
Обоснование
Заметим, что данный алгоритм отличается от предыдущего тем, что основной цикл идёт не по вершинам, по цветам : сначала , всё, что можно, красим в цвет 1 , затем в оставшиеся краски, всё, что можно в цвет 2 , и т.д. Алгоритмы В и С аналогичны.
Литература
-
Кристофидес. Теория графов. Алгоритмический подход, изд-во Мир, М ,1978
-
Ф.А. Новиков. Дискретная математика для программистов , С.П-б : Литература 2002-304-С
-
Свален М. Тхуласираман К. Графы , сети и алогитмы.М; Мир , 1984;
-
Р.Уилсон. Введение в теорию графов , Мир, М.1977.
