
1-й сем-ДМ-слайды-ДГТУ / Графы, л.5-7 / Решение задач теории графов
.docРешение задач теории графов, сформированных в виде задачи УЛП
1. Задача о минимальном внешне устойчивом подмножестве.
Подмножество вершин
![]() графа G=(A,Г)
называется внешне устойчивым, если
любая вершина
графа G=(A,Г)
называется внешне устойчивым, если
любая вершина
![]() ,
не принадлежащая
,
не принадлежащая
![]() связана по крайней мере с одной вершиной
из
связана по крайней мере с одной вершиной
из![]() дугой, начало которой лежит в
дугой, начало которой лежит в
![]() -
-![]() ,
то есть:
,
то есть:
![]() (2). Если внешне устойчивое подмножество
не содержит строго никакого другого
внешне устойчивого подмножества, то
оно называется минимальным или предельным.
Часто имеет смысл рассматривать
предельное внешне устойчивое подмножество,
содержащее минимум аргументов.
(2). Если внешне устойчивое подмножество
не содержит строго никакого другого
внешне устойчивого подмножества, то
оно называется минимальным или предельным.
Часто имеет смысл рассматривать
предельное внешне устойчивое подмножество,
содержащее минимум аргументов.
Сформулируем задачу в терминах УЛП.
Сопоставим вершины
![]() графа G(A,Г)
двоичные переменные
графа G(A,Г)
двоичные переменные![]() .
Вершина
.
Вершина
![]() тогда и только тогда, когда,
тогда и только тогда, когда,
![]() следовательно однозначно определение
ответствующее подмножество вершин
графа. Поскольку находящееся минимальное
внешне устойчивое подмножество имеет
смысл рассматривать целевую функцию в
виде:
следовательно однозначно определение
ответствующее подмножество вершин
графа. Поскольку находящееся минимальное
внешне устойчивое подмножество имеет
смысл рассматривать целевую функцию в
виде:
![]() ,
где n – число вершин графа
G=(A,Г) условие
,
где n – число вершин графа
G=(A,Г) условие![]() имеет вид в терминах УЛП:
имеет вид в терминах УЛП:
![]() i = ,n (2)
i = ,n (2)
![]()
![]() ,
i = 1,n
(3)
,
i = 1,n
(3)
Замечание: Условие (2) можно представить в виде:
![]() ,
i = 1,n
,
i = 1,n
![]() ,
где
,
где
![]() - булева матрица, построенная исходя из
матрицы, смежности графа G=(A,Г)
и условия (2).
- булева матрица, построенная исходя из
матрицы, смежности графа G=(A,Г)
и условия (2).
2. Минимальное покрытие простого графа.
Граф
![]() )
– простой, если
)
– простой, если
-
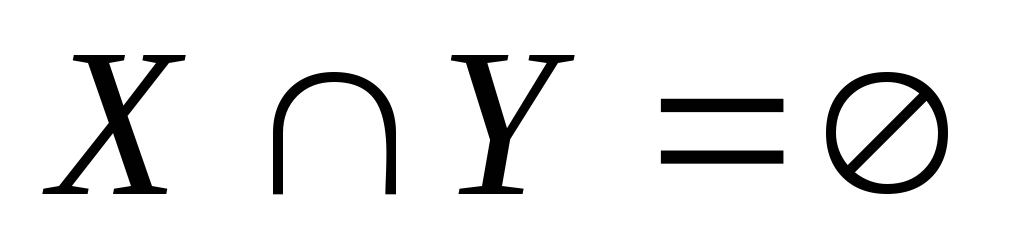
-
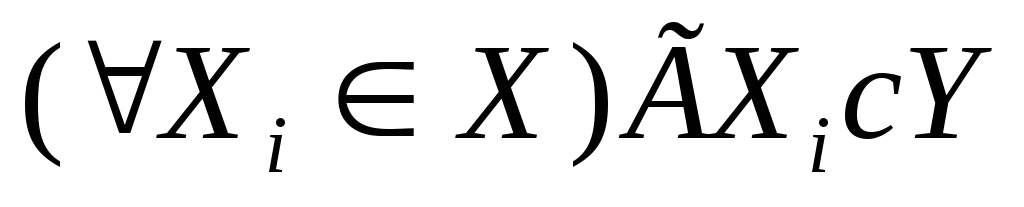 или
или
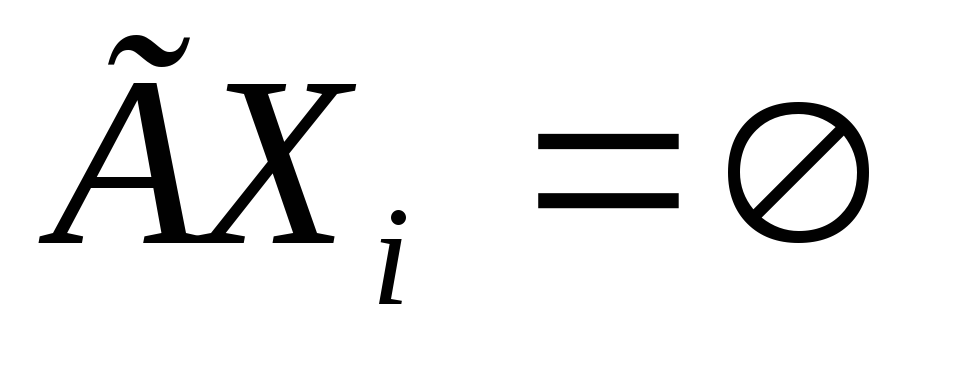
-
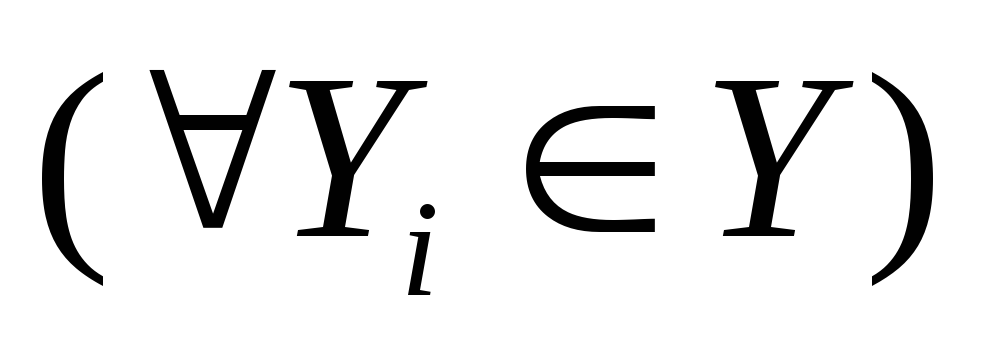
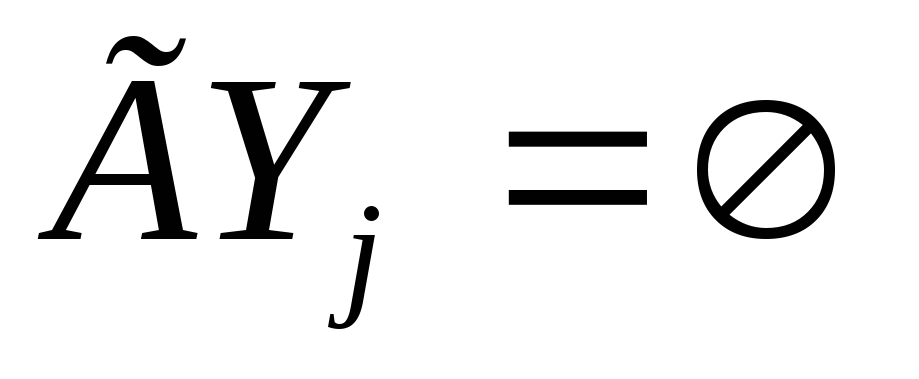
Подмножество дуг W c U графа G=(X,Y,Г)=(X,Y,U)
Называется покрытием простого графа, если любая вершина графа инцидентна по крайней мере одной дуге из W.
Часто требуется найти покрытие с
наименьшим числом дуг. Можно обобщить
задачу. Рассматривается произвольный
граф G=(X,U).
Покрытием графа (X,U)
называется такое множество его ребер
W c U,
что каждая вершина
![]() инцидентна хотя бы одному ребру из W.
Обычно ищется покрытие с наименьшим
числом ребер. Если
инцидентна хотя бы одному ребру из W.
Обычно ищется покрытие с наименьшим
числом ребер. Если
![]() – матрица инцидентна для графа G,
то в терминах УЛП задача формулируется
следующим образом:
– матрица инцидентна для графа G,
то в терминах УЛП задача формулируется
следующим образом:
Пусть
![]() - ребра графа.
- ребра графа.
![]() (1)
(1)
![]() i = 1, m (2)
i = 1, m (2)
![]()
Ясно, что элементы
![]() =
=
![]()
Замечание. Если кроме того, каждой дуге приписать стоимость, то (1) примет вид:
![]() (1’)
(1’)
3. Максимальное паросочетание простого графа.
Пусть G=(X,Y,G)=(X,Y,U)
– простой граф, в котором существую
подмножества A c
X и B c
Y такие, что
![]()
Паросочетанием, отображающем А и В
называется взаимооднозначное отображение
![]() подмножеств А параллельно В такое, что
подмножеств А параллельно В такое, что![]() ,
то есть, паросочетание простого графа
– такое множество W его
дуг, в котором 2 дуги не смежны. Максимальное
паросочетание – паросочетание с
максимально допустимым числом дуг.
,
то есть, паросочетание простого графа
– такое множество W его
дуг, в котором 2 дуги не смежны. Максимальное
паросочетание – паросочетание с
максимально допустимым числом дуг.
![]()
![]() - вершин G.
- вершин G.
Можно рассматривать паросочетание
произвольного графа G=(X,U).
Аналогично можно рассматривать
паросочетание произвольного графа
G=(X,N).
Если
![]() - матрица инцеденции для графа G,
то в терминах УЛП задача о максимальном
паросочетании произвольного графа
имеет вид:
- матрица инцеденции для графа G,
то в терминах УЛП задача о максимальном
паросочетании произвольного графа
имеет вид:
![]() (1)
(1)
![]() ,
j = 1,2,,,,m (2)
,
j = 1,2,,,,m (2)
![]() ,
i = 1,n (3)
, где
,
i = 1,n (3)
, где
![]() - булевы переменные соответствующие
ребрам графа,
i
= 1,n .
- булевы переменные соответствующие
ребрам графа,
i
= 1,n .
![]() - вершины графа, при этом
- вершины графа, при этом
![]() множество S(J)
=
множество S(J)
=
![]() ,
то есть S(J)
– множество номеров ребер, инцедентных
вершине
,
то есть S(J)
– множество номеров ребер, инцедентных
вершине
![]() .
.
Пример задачи о паросочетании – задача
о назначении лиц на должности. Если
![]() - работники,
- работники,
![]() - должности и если ГХ
- должности и если ГХ![]() - множество должностей, которые можно
занять, то нужно рассмотреть нахождение
паросочетания простого графа (X,Y,Г).
Можно задачу обобщить. Если же работников
m, должности, ценность
работников
- множество должностей, которые можно
занять, то нужно рассмотреть нахождение
паросочетания простого графа (X,Y,Г).
Можно задачу обобщить. Если же работников
m, должности, ценность
работников
![]() на должности
на должности
![]() равна
равна
![]() ,
,
![]() - булева матрица матрица назначения
m
- булева матрица матрица назначения
m![]() n.
И если:
n.
И если:
![]() (4),
то задача будет иметь вид:
(4),
то задача будет иметь вид:
![]() (1)
(1)
![]() ,
i = 1,n . (2)
,
i = 1,n . (2)
![]() ,
i = 1,m . (3)
,
i = 1,m . (3)
(1)-(3) – транспортные задачи. Если n![]() m
можно свести к n=m
присоединением к матрице m-n
нулевых либо строк (m<n),
либо столбцов(M>N).
m
можно свести к n=m
присоединением к матрице m-n
нулевых либо строк (m<n),
либо столбцов(M>N).
4. Задача о максимальном внутренне устойчивом подмножестве.
Если задан граф
G=(A,Г),
то подмножество В с А называется внутренне
устойчивым, если
![]() ,
то есть две вершины В не смежны. Внутренне
устойчивое подмножество, не являющееся
собственным подмножеством другого
внутренне устойчивого подмножества,
называется максимальным. Имеет смысл
рассматривать внутренне устойчивое
подмножество, содержащее наибольшее
число элементов. Сопоставим вершины
графа
,
то есть две вершины В не смежны. Внутренне
устойчивое подмножество, не являющееся
собственным подмножеством другого
внутренне устойчивого подмножества,
называется максимальным. Имеет смысл
рассматривать внутренне устойчивое
подмножество, содержащее наибольшее
число элементов. Сопоставим вершины
графа
![]() с двоичными переменными
с двоичными переменными
![]() .
Вершина
.
Вершина
![]() тогда и только тогда, когда
тогда и только тогда, когда
![]() ,
следовательно, соблюдается однозначность.
Так как находим максимальное внутренне
устойчивое подмножество, то целевая
функция будет иметь вид:
,
следовательно, соблюдается однозначность.
Так как находим максимальное внутренне
устойчивое подмножество, то целевая
функция будет иметь вид:
![]() (1)
(1)
n – число вершин графа.
Из самого определения внутренней устойчивости следует:
![]() i = 1, m (2)
i = 1, m (2)
m - число ребер исходного графа.
![]() - транспортная матрица инцедентности
исходного графа.
- транспортная матрица инцедентности
исходного графа.
![]() j = 1, n (3)
j = 1, n (3)
Ясно, что максимальных внутренне устойчивых подмножеств может быть несколько.
ЯДРО ГРАФА.
Найдя внутренне и внешне устойчивые подмножества, легко найти и ядро графа – подмножество, одновременно внутренне и внешне устойчивое. Граф может обладать нескольким ядрами, и может вообще не иметь ни одного.
5. Факторы графа.
Факторами графа (Х,Г) называется частичный
граф (Х,Г) с полустепенями исходя из
захода каждой вершины равный 1. Пусть
каждой дуге
![]() графа G(X,Г)
сопоставима двоичная переменная
графа G(X,Г)
сопоставима двоичная переменная
![]() .
Если дуга
.
Если дуга![]() принадлежит
графу (Х,Г), то соответствующие компоненты
принадлежит
графу (Х,Г), то соответствующие компоненты
![]() =1.
Пусть
=1.
Пусть![]() - матрица смежности рассматриваемого
графа. Очевидно, что условие
- матрица смежности рассматриваемого
графа. Очевидно, что условие
![]() и
и
![]() можно записать в виде:
можно записать в виде:
![]() i = 1, n (2)
i = 1, n (2)
![]() j = 1, n
j = 1, n
Условие формулы имеет вид:
![]() (1)
(1)![]()
Можно видеть, что при минимуме (1) всякое решение определяет фактор. Если же минимум (1) превышает n, то граф не имеет факторов.
Задача (2) - распределительная задача. Решение задачи о раскраске и кроматическом числе графа сводится к нахождению максимальных внутренне устойчивых подмножеств. Очевидно, что вершины окрашенные одинаково, образуют внутренне устойчивое подмножество. Несложно находится1111 тело или минимальное число внутренне устойчивых подмножеств, покрывающих в совокупности все вершины графа.
6. Минимальная опора простого графа.
Дан простой граф G=(X,Y,Г).
Множество S c
![]() такое, что каждая дуга
такое, что каждая дуга
![]() имеет по крайней мере одну из своих
граничных вершин в S
называемых опорой простого графа.
Минимальная опора – опора с минимальным
количеством элементов. Из определения
опоры следует, чтодополнение и опора –
внутренне устойчивое подмножество и
наоборот. Следовательно, если найти
минимальное внутренне устойчивое
подмножество В, то S
=
имеет по крайней мере одну из своих
граничных вершин в S
называемых опорой простого графа.
Минимальная опора – опора с минимальным
количеством элементов. Из определения
опоры следует, чтодополнение и опора –
внутренне устойчивое подмножество и
наоборот. Следовательно, если найти
минимальное внутренне устойчивое
подмножество В, то S
=
![]() \В
– минимальная опора. Ясно, что граф
может обладать несколькими минимальными
опорами.
\В
– минимальная опора. Ясно, что граф
может обладать несколькими минимальными
опорами.
7.Алгоритм решения задачи УЛП.
![]() (1)
(1)
![]() ,
i = 1,m (2)
,
i = 1,m (2)
![]() j = 1, m (3)
j = 1, m (3)
![]() ,
j = 1, n
,
j = 1, n
![]() ,
i = 1,m, j = 1, n (4)
,
i = 1,m, j = 1, n (4)
![]() i = 1, n (5)
i = 1, n (5)
Пусть
![]() - количество единиц в j –м
столбце
- количество единиц в j –м
столбце
![]() ,
i = 1, m, j
= 1, n.
,
i = 1, m, j
= 1, n.
Пусть
![]() ,
j = 1, n (6).
,
j = 1, n (6).
Нужно учесть 2 условия.
-
Так как вектор решения Х – булев, то из (1) следует: чем меньше
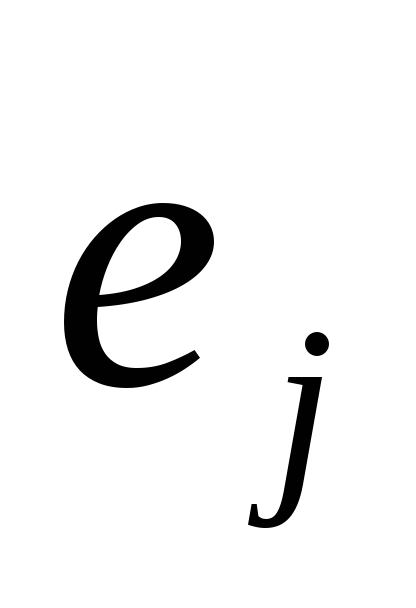 ,
тем целесообразнее соответствующую
компоненту
,
тем целесообразнее соответствующую
компоненту
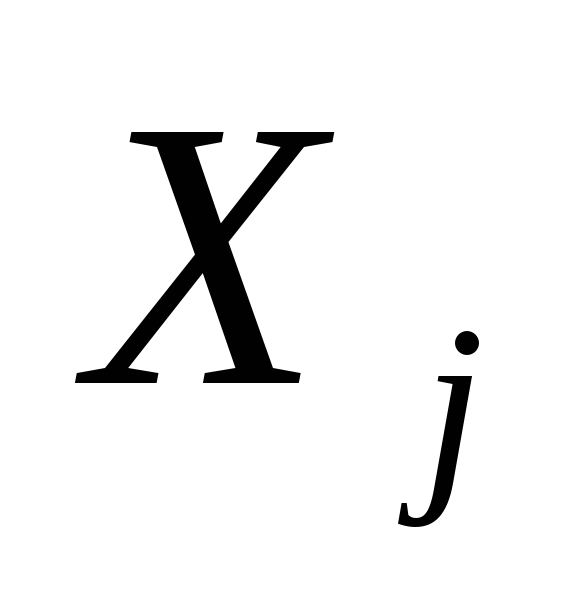 положить равной 1, j = 1,
n.
положить равной 1, j = 1,
n. -
Желательно, чтобы переменную, которую выберем была равна 1, входила в возможно большее число условий (2), то есть при этом исходим из как можно большей величины
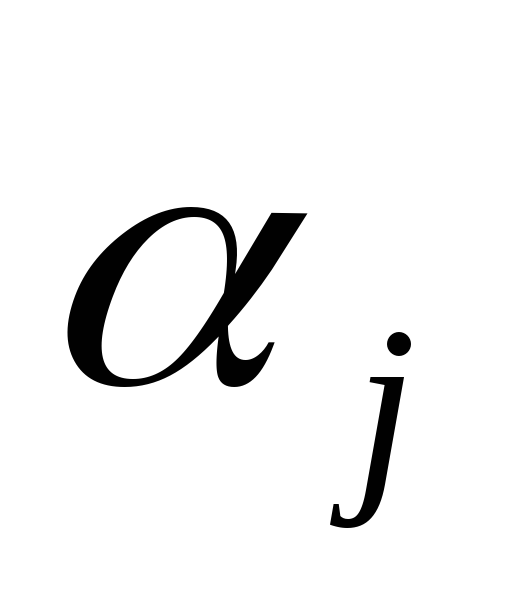 ,
j = 1.n
,
j = 1.n
Учитывая сказанное, введем отношение
![]() ,
j = 1, n
,
j = 1, n
Шаг 1. Если в некоторых стоках U1,U2,,,Un
матрицы имеем лишь по 1-ой единице в
столбцах
![]() ,
то компонента
,
то компонента
![]() ,
что следует из (2). Если (2) выполняется,
то конец. Если нет, то переходим на щаг
2.
,
что следует из (2). Если (2) выполняется,
то конец. Если нет, то переходим на щаг
2.
Шаг 2. В
![]() вычеркнем строки
вычеркнем строки
![]() столбцы
столбцы
![]() они становятся нулевыми. Получим
они становятся нулевыми. Получим
![]() .
.
Строки вектора
![]() :
:
![]() =
=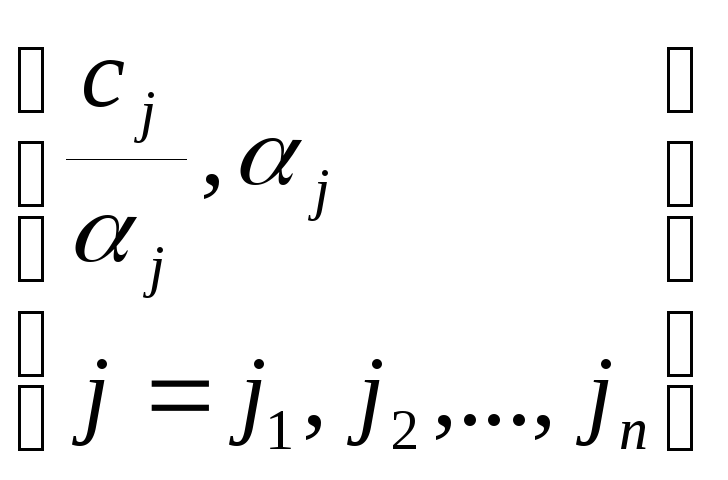
Замечание.
![]()
![]() показывает,
что в j-ом столбце
показывает,
что в j-ом столбце
![]() нет ни одной вершины, но соответствует
компонента
нет ни одной вершины, но соответствует
компонента
![]() ,
с ценой
,
с ценой
![]() может быть равна 0 или 1. рассмотрим
оставшиеся строки
может быть равна 0 или 1. рассмотрим
оставшиеся строки
![]() .
В
.
В
![]() выберем минимальную компоненту, пусть
это будет
выберем минимальную компоненту, пусть
это будет
![]() ,
тогда
,
тогда
![]() =1.
Если несколько , то за единицу принимаем
каждую из них
=1.
Если несколько , то за единицу принимаем
каждую из них
Пример:
![]()
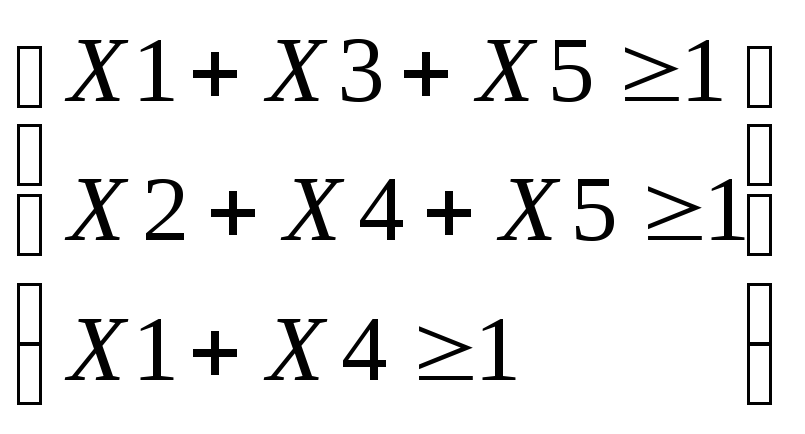 ,
то
,
то
![]() будет иметь вид:
будет иметь вид:
![]() =
=
Находим E’
E’=![]()
Так как min компоненте, то
полагаем X![]() =1
=1
Строки матрицы:
![]() =
=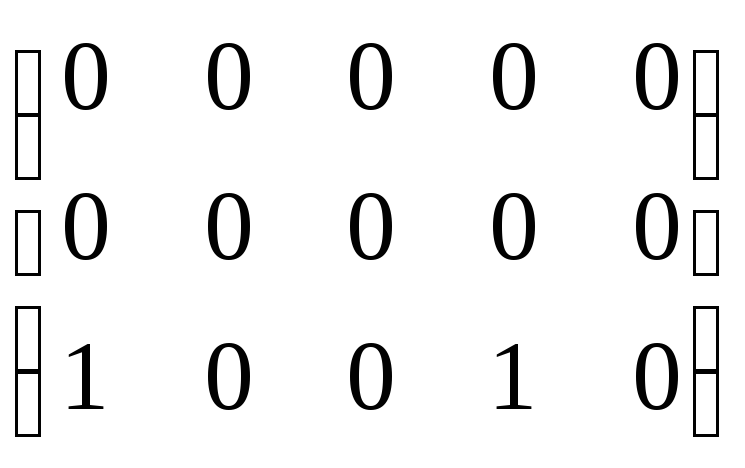
Так как С1 с С4 (![]() ),
то
),
то
![]() .
.
Нетрудно видеть, что Х=![]() удовлетворяет (2,3) и достигает min
(1), равный 4.
удовлетворяет (2,3) и достигает min
(1), равный 4.
