1-й сем-ДМ-слайды-ДГТУ / Графы-3,4 лекции / Маршруты

Маршруты, цепи и простые цепи.

Пусть G – неориентированный граф. Маршрут в G – конечная или бесконечная последовательность ребер S=(...E₀, E₁..,E_n...), в которой два соседних ребра E_i-1 и E_i имеют общую концевую точку, т. е. ...,E₀=(A₀, A₁), E₁₌(A₁, A₂)...,E_n=(A_n, A_n+1)... Одно и тоже ребро E может встречаться в маршруте несколько раз.

A₀ – начальная вершина – нет ребер перед ней; А₃ –

конечная вершина – нет ребер после нее!

Любая вершина, принадлежащая двум соседним ребрам E_i-1 и E_i, называется внутренней или промежуточной вершиной. Так как ребра и вершины в маршруте могут повторяться, внутренняя вершина может оказаться начальной или конечной вершиной. Маршрут называется нетривиальным, если он содержит хотя бы одно ребро; маршрут не содержащий никаких ребер, называется нуль – маршрутом.

Если маршрут S имеет начальную вершину A₀ и конечную вершину A_n, то

S=S(A₀, A_n), A₀ и A_n – концевые точки или концы маршрута S. Говорят, что S – маршрут длины n, соединяющий A₀ и A_n. Если А₀=А_n, то маршрут называется циклическим.

Для двух вершин маршрута A_i и A_j подмаршрут S(A_i, A_j)=(E_i, E_i+1,...,E_j-1) называется конечным участком S.

Маршрут называется цепью, а циклический маршрут – циклом, если каждое его ребро встречается в нем не более одного раза; вершины в цепи могут повторяться и несколько раз. Любой участок цепи есть цепь.

Нециклическая цепь называется простой цепью, если в ней никакая вершина не повторяется. Цикл с концом А₀ называется простым циклом, если А₀ не является в нем промежуточной вершиной и никакие другие вершины не повторяются. Участок простой цепи (цикла) – простая цепь (цикл). Для ориентированного графа можно вводить как неориентированные маршруты, цепи и простые цепи, не принимая во внимание ориентации ребер, так и ориентированные маршруты, цепи, простые цепи, в которых все ребра проходятся в направлении их ориентации. Ориентированную цепь называют путем, ориентированный цикл – контуром.

Граф G называется связным, если для любых двух его вершин V и W существует простая цепь из V в W.

Любой граф можно разбить на непересекающиеся связные подграфы, называемые компонентами (связности), задав отношение эквивалентности на множестве его вершин: две вершины эквивалентны (или связны), если существует простая цепь из одной в другую. Связный граф состоит из одной компоненты. Граф несвязный, если число его компонент больше единицы.

Если имеем граф с n вершинами, заданным числом компонент. Если граф связан, то число ребер в нем минимально, когда он не имеет циклов (такой граф называется деревом) и максимальным, когда он – полный граф. Число ребер в таком графе m:

;

Теорема: Пусть G – простой граф с n вершинами и k компонентами. Тогда число m его ребер:

Доказательство: неравенство докажем индукцией по числу ребер в G. Если G – вполне несвязный граф, то утверждение очевидно . Если в графе G число ребер минимально (M₀), то удаление любого ребра должно привести к увеличению числа компонент на единицу. Таким образом, в получившемся графе будет m вершин, k+1 компонент и M₀-1 ребер. Следовательно, в силу индуктивного предположения , откуда получается , что и утверждалось.

Для доказательства оценки сверху считаем каждую компоненту графа G полным графом. Пусть С_i и C_j – две компоненты соответственно с n_i и n_j вершинами и >1 Если мы заменим С_i и С_j на полные графы с и вершинами, то общее число вершин не изменится, а число ребер увеличится на положительную величину:

Следовательно, для того, чтобы число ребер в G было максимально возможным (при заданных n и k), G должен состоять из k-1 изолированных вершин и сложного графа с n-k+1 вершинами, что и требовалось доказать.

Следствие: Любой простой граф с n вершинами и более, чем ребрами связан.

Насколько же сильно связен связный граф? Т.е. сколько ребер нужно удалить из графа, чтобы он перестал быть связным? Разделяющее множество связного графа G – множество его ребер, удаление которого приводит к неверному графу. Например, в графе каждое из множеств и являемое разделяющим; неверный граф, оставшийся после удаления второго из этих множеств, имеет вид:

l₃

l₅ l₆ l₄ l₄

l₁ l₁ l₅

l₇

l₂ l₈ l₂

Назовем разрезом такое разделяющее множество, никакое собственное подмножество которого не является разделяющим.

Разрезом является множество . После удаления ребер, принадлежащих разрезу, остается граф имеющий ровно 2 компоненты. Если разрез состоит из 1 ребра l, то l называется мостом или перешейком.

В произвольном графе G, разделяющее множество – множество ребер, удаление которого увеличивает число компонент в G. Разрез в G – разделяющее множество, никакое собственное подмножество которого не является разделяющим.

мост

l

Теорема: Если в конечном графе G ровно две вершины a₀ и b₀ имеют нечетную локальную степень, то они связаны.

Доказательство: Каждый конечный граф имеет четное число вершин, нечетной степени. Так как это условие выполняется и для этой компоненты G, которой принадлежит a₀, то b₀ должно принадлежать той же компоненте.Кроме того, a₀ и b₀ должны остаться связными в графе , полученном из G удалением части H, которой все локальные степени четные .

Теорема: Если граф G с однократными ребрами и без петель имеет n вершин и k связных компонент, то максимальное число ребер в G равно (2)

Доказательство: Пусть в графе G компонента G_i имеет N_i вершин. Тогда максимальное число ребер в G равно..Это число достигается тогда, когда каждый из графов G_i полный и имеет n_i вершин. Допустим ,что среди графов G_i найдутся хотя бы 2, которые имеют более одной вершины, например . Построим вместо G другой граф с тем же числом вершин и компонент, заменяя и полным графом и соответственно с и вершинами. Это увеличивает число ребер. Итак максимальное число ребер должен иметь граф, состоящий из k-1 изолированных вершин и одного полного графа с n-k+1 вершинами. Его число ребер описывается формулой (2). Для случая k>2 имеем: граф с n вершинами и с числом ребер, больше чем связан.

Можно учитывать и пропускные способности и надежности дуг.

Кратчайший путь между двумя заданными вершинами s и t.

Рассмотрим случай

Алгоритм Дейкстры. Он основан на приписывании вершинам временных пометок, причем пометка вершины дает верхнюю границу длины пути от s к этой вершине. Эти пометки (их величины) постепенно изменяются с помощью некоторой итерационной процедуры, и на каждом шаге итерации точно одна из временных пометок становится постоянной. Это указывает на то, что пометка уже не является верхней границей, а дает точную длину кратчайшего пути от s к рассматриваемой вершине.

Пусть - пометка вершины .

Присвоение начальных значений.

Шаг 1. Положить и считать эту пометку постоянной. Положить для всех и считать эти пометки временными. Положить p=s.

Обновление пометок.

Шаг 2. Для всех , пометки которых временные, изменить пометки в соответствии со следующим выражением: .

Превращение пометки в постоянную .

Шаг 3. Среди всех вершин с временными пометками найти такую, для которой

Шаг 4. Считать пометку вершины постоянной и положить .

Шаг 5. a) (Если нужно найти лишь путь от s к t). Если p=t, то - длина кратчайшего пути. Остановка. Если , перейти к шагу 2.

b) (Если требуется найти пути от s ко всем остальным вершинам).

Если все вершины отмечены как постоянные, то эти пометки дают длины кратчайших путей. Остановка.

Если некоторые пометки являются временными, перейти к шагу 2.

Доказательство.

Допустим, что на некотором этапе постоянные пометки дают длины кратчайших путей. Пусть - множество вершин с этими пометками, а - множество вершин с временными пометками. В конце шага 2 каждой итерации временная пометка дает кратчайший путь от s к , проходящий полностью по вершинам множества . Так как при каждой итерации в множество включается только одна вершина, то обновление пометки требует только одного сравнения на шаге 2. Пусть кратчайший путь от s к не проходит целиком по и содержит по крайней мере одну вершину из , и пусть - первая такая вершина в этом пути. Так как , то часть пути от к должна иметь не отрицательный вес и . Это, однако, противоречит утверждению, что - наименьшая временная пометка, и, следовательно, кратчайший путь к проходит полностью по вершинам множества , и поэтому является его длиной. Так как множество равно и при каждой итерации к добавляется , то предположение, что равно длине кратчайшего пути , выполняется при каждой итерации. Отсюда по индукции следует, что алгоритм дает оптимальный ответ.

Если требуется найти кратчайшие пути между s и всеми другими вершинами полного связного графа с n вершинами то в процессе работы алгоритма выполняется операций сложения и сравнения на шаге 2 и еще операций сравнения на шаге 3.

Кроме того, при осуществлении шагов 2 и 3 необходимо определить, какие вершины являются временными, а для этого нужно еще операций сравнения. Эти величины являются верхними границами для числа операций, необходимых при отношении кратчайшего пути между заданными вершинами s и t. Они действительно достигаются, если окажется, что вершина t будет последней вершиной, получившей постоянную пометку.

Как только длины кратчайших путей от s будут найдены (они будут заключительными значениями пометок вершин), сами пути можно получить при помощи рекурсивной процедуры: . Так как вершина непосредственно предшествует вершине в кратчайшем пути от s к , то для любой вершины соответствующую вершину можно найти как одну из оставшихся вершин, для которой имеем .

Если кратчайший путь от S до является единственным, то дуги этого кратчайшего пути .Если существует немного кратчайших путей от S к какой – либо другой вершине то при некоторой фиксированной вершине (2) будет выполнено для более чем одной вершины . В этом случае выбор может быть, либо произвольным (если нужен какой-то 1 кратчайший путь между s и ), либо таким что рассматриваются все дуги , входящие в какой-либо из кратчайших путей, и при этом ? всех таких дуг образует неориентированное дерево, а общий граф, называемый базой относительно S или кратко S-базой.

Пример.

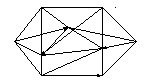
Рассмотрим граф G где каждое неориентированное ребро рассматривается как пара противоположно ориентированных дуг равного веса.

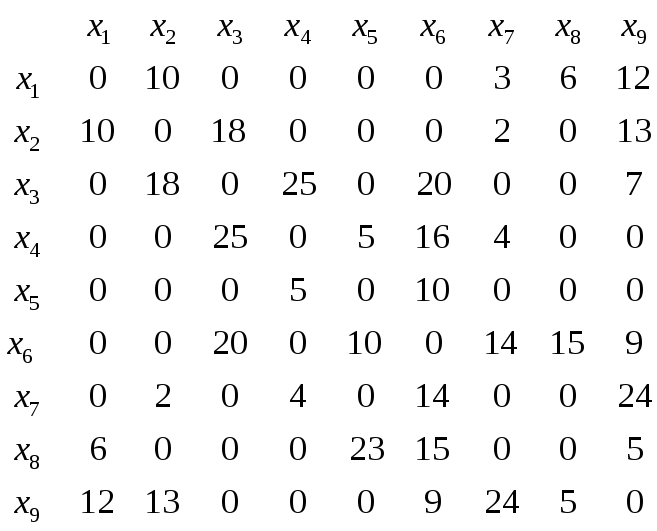
Матрица

Решаем алгоритм Дейкстры.

Постоянные пометки снабжаем знаком +, остальные пометки временные.

Алгоритм работает так:

Шаг 1. , .

Первая итерация.

Шаг 2. - все пометки временные. Возьмем из : ; ;

Шаг 3. соответствует

Шаг 4. получает постоянную пометку

Шаг 5. Не все вершины имеют постоянные пометки, поэтому переходим к шагу 2. Пометки в ? покажем в графе:

рис.1

Вторая итерация.

Шаг 2. - все пометки временные. Из ? имеем: ; ;; Получим ? рис.1

Шаг 3. соответствует

Шаг 4. получает постоянную пометку

Шаг 5. Перейти к шагу 2.

Третья итерация.

Шаг 2. - точно вершины и имеют временные пометки; из соотношения получаем: и аналогично

Шаг 3. соответствует

Шаг 4. получает постоянную пометку

Шаг 5. Перейти к шагу 2.

Продолжая этот процесс, получим:

Для нахождения кратчайшего пути между вершиной (например) и начальной вершиной мы последовательно используем соотношение . Таким образом, ?? , находим вершину , непосредственно предшествующую в кратчайшем пути от к : вершина должна удовлетворять соотношению: . Единственной такой вершиной является . Далее применяя , беря получаем вершину , непосредственно предшествующую в кратчайшем пути от к . Вершина удовлетворяет: .

Единственная такая вершина поэтому кратчайший путь от к есть . - база, дающая все кратчайшие пути от дерево, изображенное жирными линиями.

Кратчайшие пути в графе.

Пусть дан граф G=(X,Г), дугам которого приписаны веса (стоимости), задаваемые матрицей . Задача о кратчайшем пути – нахождение кратчайшего пути от заданной от заданной начальной вершины до заданной конечной вершины , при условии, что такой путь существует, т.е. при условии . - множество, достижимое из вершины S. Элементы матрицы C могут быть >0, <0, =0. Единственное ограничение – в G ??циклов с ?? отрицательным весом. Если такой цикл Ф и - его вершина, то двигаясь от S к , обходя затем Ф достаточно большое число раз и попадая наконец в t, получая путь со сколь угодно малым весом. Таким образом, в этом случае кратчайшего пути не существует.

Если такие длины существуют , но исключаются из рассмотрения, то нахождение кратчайшего пути (простой цепи) между s и t эквивалентно нахождению в этом графе кратчайшего гамильтонова пути с концевыми вершинами s и t. Это видно из следующей ???. Если из каждого элемента матрицы весов С вычесть достаточно большое число L, то получается новая матрица весов , все элементы которой отрицательны. Тогда кратчайший путь от s к t – с исключением отрицательных циклов – необходимо будет ???

Так как вес любого гамильтонова пути с матрицей С, но уменьшенному на постоянную величину (n-1)L , то кратчайший путь (простая цепь) от s к t с матрицей будет кратчайшим гамильтоновым путем ??? s к t при первоначальной матрице С. Задача нахождения кратчайшего гамильтонова пути намного сложнее чем задача о кратчайшем пути. Поэтому будем предполагать, что все длины в G имеют неотрицательный суммарный вес. Отсюда следует, что неориентированные дуги (ребра) графа G не могут иметь отрицательного веса.

Возникает следующая задача:

1. Для заданной начальной вершины S найти кратчайшие пути между S и всеми другими вершинами

2. Найти кратчайшие пути между всеми парами вершин.

Матрица весов не удовлетворяет условию треугольников, т.е., не обязательно для всех i, j и k. В противном случае кратчайший путь между и x состоит из одной единственной дуги (если она существует) и задача становится тривиальной. Если в графе G дуга отсутствует, то ее вес покажется равным .

На практике требуется найти не только кратчайший путь, но второй третий и т.д. подкратчайшие пути.