
§ 4.13. Векторные пространства,
связанные с графами
Рассмотрим
алгебраическую систему
 2=
2= с двухместными операциями кольцевого
сложения⊕
и умножения ⊙,
задаваемыми следующими правилами:
0⊕0=1⊕1=0,
1⊕0=0⊕1=1,
0⊙0=0⊙1=1⊙0=0,
1⊙1=1.
Система
с двухместными операциями кольцевого
сложения⊕
и умножения ⊙,
задаваемыми следующими правилами:
0⊕0=1⊕1=0,
1⊕0=0⊕1=1,
0⊙0=0⊙1=1⊙0=0,
1⊙1=1.
Система
 2
является
булевым кольцом (см.§2.6) и, более того,
образует поле.
2
является
булевым кольцом (см.§2.6) и, более того,
образует поле.
Пусть
G=
 связный
неорграф, имеющий n
вершин и m
ребер
связный
неорграф, имеющий n
вершин и m
ребер
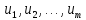 .
Произвольному множеству реберA
.
Произвольному множеству реберA
 R
поставим в соответствие вектор
R
поставим в соответствие вектор
 =
= ,
положив
,
положив

Каждому
множеству ребер соответствует
единственный вектор, состоящий из нулей
и единиц, а для любого набора
 нулей и единиц найдется единственное
множество ребер, соответствующее этому
набору. Таким образом, существует биекция
между булеаном множества реберR
и множеством всех наборов длины m,
состоящих из нулей и единиц: P
(R)↔
нулей и единиц найдется единственное
множество ребер, соответствующее этому
набору. Таким образом, существует биекция
между булеаном множества реберR
и множеством всех наборов длины m,
состоящих из нулей и единиц: P
(R)↔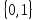 m.
Пусть
m.
Пусть
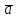 =
= и
и =(
=( )-
наборы (векторы) из
)-
наборы (векторы) из m.
Определим сложение векторов с помощью
соотношения
m.
Определим сложение векторов с помощью
соотношения
 ⊕
⊕ =(
=(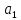 ⊕
⊕ ,
… ,
,
… , ⊕
⊕ )по правилам,
определенным в поле
)по правилам,
определенным в поле
 2.
Кроме этого,
определим произведение векторов на
элементы
2.
Кроме этого,
определим произведение векторов на
элементы

 ,
положив λ⊙
,
положив λ⊙
 =(λ⊙
=(λ⊙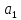 ,
… ,λ⊙
,
… ,λ⊙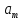 ).
Множество векторов
).
Множество векторов m
с операциями сложения ⊕
и умножения ⊙
на элементы поля
m
с операциями сложения ⊕
и умножения ⊙
на элементы поля
 2
образует
линейное пространство над полем
2
образует
линейное пространство над полем
 2.
Это пространство
обозначим через
2.
Это пространство
обозначим через
 (
( 2).
2).
Отметим, что
сложение ⊕
векторов
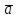 и
и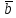 соответствует кольцевой сумме множеств
реберA
и B,
представляемых этими векторами.
Действительно, равенство
соответствует кольцевой сумме множеств
реберA
и B,
представляемых этими векторами.
Действительно, равенство
 выполняется тогда и только тогда, когда
выполняется тогда и только тогда, когда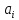 =1,
=1, (т.е.
(т.е. или
или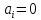 ,
, (т.е.
(т.е. .
Следовательно, сумме
.
Следовательно, сумме ⊕
⊕ соответствует
множество (A\B)
соответствует
множество (A\B) (B\A)=A⊕B.
(B\A)=A⊕B.
Внутреннее
произведение векторов
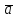 =
= и
и =(
=( определяется соотношением (
определяется соотношением (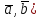 =
= Равенство (
Равенство ( =0
означает, что четное число произведений
=0
означает, что четное число произведений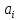 ⊙
⊙ равно 1.
Для таких произведений
равно 1.
Для таких произведений
 =1,
=1, и, следовательно, соответствующие
векторам
и, следовательно, соответствующие
векторам и
и множества реберA
и B
имеют четное число общих ребер.
множества реберA
и B
имеют четное число общих ребер.
Множество ребер
A
называется границей (кограницей),
если A
есть объединение множеств ребер некоторых
циклов (коциклов), из которых любые два
множества не имеют общих ребер. Нетрудно
заметить, что кольцевая сумма A1⊕
A2
также является границей (кограницей).
Следовательно, множества VГ= соответствует
некоторой
соответствует
некоторой иVK
=
иVK
=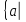 вектор
вектор соответствует некоторой
соответствует некоторой образуют линейные подпространства
пространстваVm
образуют линейные подпространства
пространстваVm
 2).
2).
Теорема
4.13.1. 1.
Если
 фундаментальное
множество циклов графа G,
то множество 𝔅С
=
фундаментальное
множество циклов графа G,
то множество 𝔅С
=
 векторов, соответствующих фундаментальным
циклам, образует базис подпространства
границVГ.
векторов, соответствующих фундаментальным
циклам, образует базис подпространства
границVГ.
2.
Если
 фундаментальное
множество коциклов графа G,
то множество 𝔅K=
фундаментальное
множество коциклов графа G,
то множество 𝔅K=
 векторов, соответствующих фундаментальным
разрезам, образует базис подпространства
кограницVK.
векторов, соответствующих фундаментальным
разрезам, образует базис подпространства
кограницVK.
Следствие
4.13.2. 1.
Размерность dim
VГ
подпространства
границ VГ
равна цикломатическому числу
 ,
а размерностьdim
VK
подпространства кограниц VK
равна корангу
,
а размерностьdim
VK
подпространства кограниц VK
равна корангу
 .
.
2.Любой цикл ( коцикл ) в графе можно представить в виде кольцевой суммы некоторых фундаментальных циклов (разрезов).
Два подпространства
V1
и V2
векторного пространства Vm
(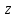 2)
называются ортогональными (V1
2)
называются ортогональными (V1 V2),
если для любых векторов
V2),
если для любых векторов
 V1
и
V1
и
 V2
их внутреннее произведение (
V2
их внутреннее произведение ( ,
, )
равно 0.
)
равно 0.
Заметим, что по
теореме 4.12.3 любой цикл C
с любым разрезом K
имеет четное число общих ребер, т.е. для
соответствующих векторов
 и
и
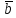 их внутреннее произведение(
их внутреннее произведение( ,
, )
равно нулю. В частности, для любых
векторов
)
равно нулю. В частности, для любых
векторов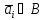 C
и
C
и
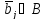 K
справедливо (
K
справедливо ( ,
, )=0.
Так как множества
)=0.
Так как множества C
и
C
и
 K
образуют базисы подпространств VГ
и VK,
то VГ
K
образуют базисы подпространств VГ
и VK,
то VГ
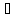 VK.
VK.
Отметим также,
что при умножении матрицы фундаментальных
циклов C
на транспортированную матрицу
фундаментальных разрезов KT
в поле
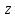 2
строка
2
строка
 умножается на столбец
умножается на столбец по правилу произведения и (
по правилу произведения и (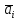 ,
, )=0.
Это означает чтоC
)=0.
Это означает чтоC KT=0,
а также K
KT=0,
а также K CT=0.
CT=0.
У п р а ж н е н и
е. Проверить, что для матриц C
и K
из примеров 4.11.1 и 4.12.1 справедливо C KT=0.
KT=0.
