
§ 4.11. Фундаментальные циклы
Пусть G= неорграф, имеющий n
вершин, m
ребер и с компонент связности, T-остов
графа G.
В §4.8 отмечалось, что T
имеет v*(G)=n-c
ребер u1,
… , un-c,
которые будем называть ветвями
остова T.
Оставшиеся m-n+с
ребер v1,
v2,
… , vm-n+c
, не входящие
в T,
будем называть хордами остова T.
Согласно теореме 4.8.1, п. 5, если к лесу T
добавить произвольную хорду vi
, то в полученном графе найдется ровно
один цикл, который обозначим через Ci.
Цикл Ci
состоит из хорды vi
и некоторых
ветвей остова T,
которые принадлежат единственной
простой цепи, соединяющей вершины хорды
vi.
Цикл Ci
называется фундаментальным
циклом графа
G
относительно хорды vi
остова T.
Множество
неорграф, имеющий n
вершин, m
ребер и с компонент связности, T-остов
графа G.
В §4.8 отмечалось, что T
имеет v*(G)=n-c
ребер u1,
… , un-c,
которые будем называть ветвями
остова T.
Оставшиеся m-n+с
ребер v1,
v2,
… , vm-n+c
, не входящие
в T,
будем называть хордами остова T.
Согласно теореме 4.8.1, п. 5, если к лесу T
добавить произвольную хорду vi
, то в полученном графе найдется ровно
один цикл, который обозначим через Ci.
Цикл Ci
состоит из хорды vi
и некоторых
ветвей остова T,
которые принадлежат единственной
простой цепи, соединяющей вершины хорды
vi.
Цикл Ci
называется фундаментальным
циклом графа
G
относительно хорды vi
остова T.
Множество
 всех фундаментальных циклов относительно
хорд остоваT
называется фундаментальным
множеством циклов
графа G
относительно остова T.
Отметим, что мощность фундаментального
множества циклов равна цикломатическому
числу v(G)=m
всех фундаментальных циклов относительно
хорд остоваT
называется фундаментальным
множеством циклов
графа G
относительно остова T.
Отметим, что мощность фундаментального
множества циклов равна цикломатическому
числу v(G)=m .
.
Обозначим
через
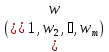 последовательность
последовательность всех ребер графаG.
Тогда фундаментальному циклу Ci
соответствует вектор
всех ребер графаG.
Тогда фундаментальному циклу Ci
соответствует вектор
 =
= ,
определенный по следующему правилу:
,
определенный по следующему правилу:

Теперь
фундаментальное множество циклов можно
задать с помощью матрицы
фундаментальных циклов,
строки которой являются векторами
 1,
1,
 2,
… ,
2,
… ,
 v(G):
v(G):
C⇌ .
.
Так
как каждый фундаментальный цикл Ci
содержит ровно одну хорду, а именно
 ,
то матрицаC
имеет вид
,
то матрицаC
имеет вид
C=
 .
.
Таким образом,
C= ,
где
,
где единичная
матрица порядка
единичная
матрица порядка .
.
П р и м е р 4 .11.1.
Найдем матрицу фундаментальных циклов
графа G,
изображенного на рис. 4.45.Так как
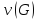 =8
=8 6+1=3,
то для получения остова удаляем из графа
три ребра. Сопоставим этим ребрам номера
1,2,3.
6+1=3,
то для получения остова удаляем из графа
три ребра. Сопоставим этим ребрам номера
1,2,3.
Ребрам,
входящим в остов, поставим в соответствие
номера 4,5,6,7,8. Легко видеть, что
фундаментальный цикл
 ,
соответствующий хорде 1, состоит из
ребер 1,4,6, цикл
,
соответствующий хорде 1, состоит из
ребер 1,4,6, цикл -из
ребер 2,6,7, циклC3-из
ребер 3,6,7,8. Поэтому матрица фундаментальных
циклов C
имеет вид
-из
ребер 2,6,7, циклC3-из
ребер 3,6,7,8. Поэтому матрица фундаментальных
циклов C
имеет вид

C .
.
5
8




4 2
6 3
1
7

рис. 4.45
