Лабораторная работа №О-6 (оптика)

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«ДОНСКОЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

КАФЕДРА ФИЗИКИ

Эффект Зеемана

Методические указания к лабораторной работе № О-6

Ростов-на-Дону 2012

1

УДК 530.1

Составители: И.В. Мардасова, Н.В. Пруцакова, А.П. Сафронов, И.В. Шкиль

Эффект Зеемана: метод. указания.– Ростов-на-Дону: Издательский центр ДГТУ, 2012. – 15 с

Методические указания предназначены для организации самостоятельной работы студентов при подготовке к лабораторному практикуму на оборудовании и фирмы «PHYWE» и рейтинговому контролю.

Печатается по решению методической комиссии факультета «Нанотехнологии и композиционные материалы»

Научный редактор д-р техн. наук, проф. В.С. Кунаков

© Издательский центр ДГТУ, 2012

2

ЛЭФ

ЭФФЕКТ ЗЕЕМАНА 5.1.10

-05

Цель работы. Изучение эффекта Зеемана с помощью спектральной лампы с кадмием, определение значения магнетона Бора.

Оборудование. 1. Электромагнит ЭМ, установленный на враща-ющемся столе, между полюсами которого находится спек- траль-ная лампа с кадмием. 2. Оптическая скамья, на которой ус- танов-лены: ирисовая диафрагма Д; линза Л1 (F1=+50 мм), ин- терфе-рометр Фабри-Перо И; линза Л2 (F2 =+300 мм); поляризатор П; линза Л3 (F3 = +50 мм); видеокамера ВК для персонального компьютера. 3. Источники питания ИП для электромагнита и спектральной лампы. 4. Цифровой мультиметр М. 5. ПК с программным обеспечением.

Рис.1. Экспериментальная установка

3

Краткая теория

Эффект Зеемана – расщепление спектральных линий под действием магнитного поля. Открыт в 1896 г. П. Зееманом при исследовании свечения паров натрия в магнитном поле.

Эффект обусловлен расщеплением энергетических уровней атома на подуровни во внешнем магнитном поле. Соответственно в спектре атома наблюдается расщепление спектральных линий. Различают нормальный и аномальный (cложный) эффекты Зеемана. Нормальный эффект возникает при расщеплении одиночной (синглетной) линии. При этом линия расщепляется на три компоненты (триплет): две - компоненты и одна - компонента.

Большинство спектральных линий представляют собой мультиплеты (состоят из двух или нескольких тесно расположенных линий). Расщепление таких мультиплетов в магнитном поле дает гораздо более сложную картину и называется аномальным (сложным) эффектом Зеемана.

В данной работе рассматривается нормальный эффект Зеемана; используется спектральная лампа с кадмием.

Атом кадмия – система с нулевым полным спином, s 0. В отсутствии магнитного поля при B 0 энергетические уровни не расщеплены и возможен только один переход (рис. 2,а) между

h6.626 10 34 Дж c- постоянная Планка.

Вмагнитном поле каждый уровень разделяется на 2l 1 подуровней (l - орбитальное квантовое число), соответствующих

возможным значениям магнитного квантового числа ml : ml 0, 1, 2,..., l. Соответственно p- уровень расщепляется на 3, а d - уровень - на 5 подуровней (рис. 2,б).

Величина расщепления Е между соседними подуровнями одинакова и пропорциональна индукции внешнего

магнитного поля B: Е BB,

где B 9.273 10 24 Дж / Тл - магнетон Бора.

4

Магнетон Бора – проекция собственного магнитного момента (спина) электрона на направление вектора B внешнего

e

магнитного поля ,

B 2m

где e 1.6 10 19 Кл - заряд электрона,

5

Частота соответствующей спектральной линии:

сопровождается излучением энергии h 0 , частота соответствую-

щей спектральной линии равна 0 , т.е. имеет такое же значение,

как и в случае, когда B = 0.

Следовательно, первоначальная спектральная линия 0

в магнитном поле расщепляется на три компоненты:

разному поляризованы, то есть поляризатором света является само магнитное поле.

Эффект расщепления спектральной линии 0 (рис.3)

можно наблюдать поочередно в двух взаимно перпендикулярных направлениях: перпендикулярно магнитному полю и вдоль поля. Вследствие различной поляризации компонент наблюдаемая картина будет различной.

При наблюдении перпендикулярно полю (поперечный

компоненте) – параллельны B (рис.3, а).

При наблюдении вдоль поля (продольный эффект Зеемана) виден дублет (две линии): 0 и 0 : первая

6

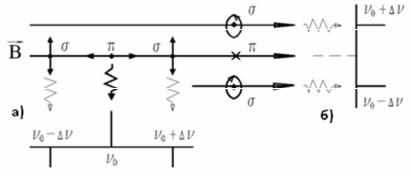
линия циркулярно поляризована по правому кругу, вторая – левополяризованная (рис.3,б).

По интенсивности - компонента в два раза больше, чем каждая из - компонент, интенсивности которых равны между собой; циркулярно-поляризованные компоненты при продольном эффекте по интенсивности совпадают с - компонентой при поперечном эффекте (рис.3).

Рис.3

Методика эксперимента

Для наблюдения эффекта Зеемана источник света - спектральная лампа, испускающая линейчатый спектр, располагается между полюсами мощного электромагнита (рис.1). Расщепление спектральных линий в магнитном поле весьма

незначительно (для магнитных полей ~ 2 106 А/ м составляет

несколько десятых Å), поэтому используются спектральные приборы с высокой разрешающей способностью.

Для количественного измерения расщепления используется интерферометр Фабри-Перо, который имеет разрешение 300000. Это позволяет определить изменение длины волны в 0,002 нм.

Интерферометр состоит из двух стеклянных пластинок, расположенных на расстоянии d друг от друга. На обращенные друг к другу плоскости нанесены высокоотражающие покрытия. Плоская волна, падающая на интерферометр, в результате

7

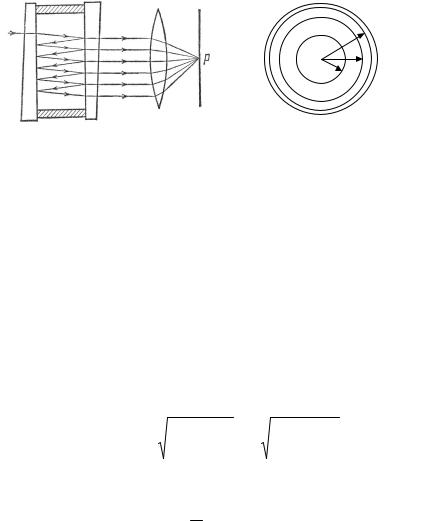
многократных отражений от пластинок и частичного выхода после каждого отражения разбивается на большое число плоских когерентных волн, отличающихся по амплитуде и по фазе (рис.4).

d

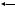f

Рис.4.

Амплитуда когерентных волн с ростом числа отражений убывает по закону геометрической прогрессии, поэтому при интерференции можно учитывать вклад только соседних волн, идущих в данном направлении. Разность хода между каждой соседней парой когерентных волн, идущих в данном направлении,

постоянна и равна

коллиматора, когерентные волны интерферируют в его фокальной плоскости и образуют пространственную интерференционную картину в виде колец равного наклона const (рис. 5).

Можно показать, что радиус кольца определяется выражением

где f – фокусное расстояние линзы объектива выходного коллиматора, c 3 108 м / с – скорость света в вакууме,

m - номер кольца, c – частота излучения.

8

Кольцо с радиусом rm после включения магнитного поля при наблюдении поперечного эффекта Зеемана разбивается на

Бора B по формуле (4), необходимо выразить разность частотa b через наблюдаемые экспериментально радиусы колец ra и rb , используя соотношение (3).

разность квадратов радиусов компоненты b для соседних колец. После соответствующих подстановок формула для расчета

магнетона Бора приобретает вид:

9

Выполнение работы

Внимание! Включение и настройка установки осуществляется обслуживающим персоналом!

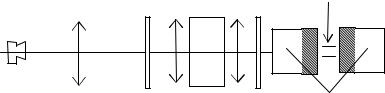
На оптической скамье расположены следующие элементы (рис.6): ирисовая диафрагма Д; линза Л1, формирующая параллельный пучок света от кадмиевой лампы; интерферометр ФабриПеро И со сменным светофильтром, через который проходит свет с длиной волны 643,8 нм; линза Л2, анализатор А и линза Л3, формирующая интерференционную картину, которая поступает в видеокамеру ВК. Радиусы колец измеряются при помощи программного обеспечения видеокамеры ВК.

ВК

*

Полюсные

наконечники

Рис.6. Расположение приборов на оптической скамье

Включите компьютер и войдите в программу «Motic Educator». Для получения изображения зайдите в меню «File»(«Файл») и выберите опцию «Capture Window» («Фотогра-фия окна»).

Установки контраста, яркости и насыщения изображения регулируются в «Video Capture Filter» («Фильтр изображения») в меню

«Options» («Опции»).

Задание 1. Изучение поперечного эффекта Зеемана.

1. Наконечники электромагнита установить перпендикулярно направлению оптической оси установки.

10