Строительная механика машин

Получаем систему уравнений нулевого приближения в связной системе координат.

Компоненты вектора есть малые углы поворота связанных осей относительно своего естественного состояния. Вектор характеризует смещение точек осевой линии стержня относительно естественного состояния.

Представим векторные произведения в виде:

Тогда получаем векторные уравнения относительно

Где

Приращения кривизны можно найти из уравнения

Для следящих нагрузок

Уравнения равновесия нулевого приближения в декартовой системе координат

Так как , то , где .

При малых углах поворота связанных осей , , тогда

Окончательно получаем следующую систему векторных уравнений, связанных с базисом {i_j}:

Здесь матрицы

Уравнения равновесия первого приближения в связанной системе координат

Положим

Векторы с индексом (1) назовем векторами первого приближения. Причем компоненты - малые величины.

Рассмотрим уравнение

Причем мало, тогда

Тогда, уравнение 0-го приближения

уравнение 1-го приближения

Где .

Векторы находятся из уравнений 0-го приближения.

Векторы находятся из уравнений 1-го приближения.

Поступая аналогично с остальными уравнениями, получаем наряду с системой уравнений 0-го приближения, систему уравнений 1-го приближения:

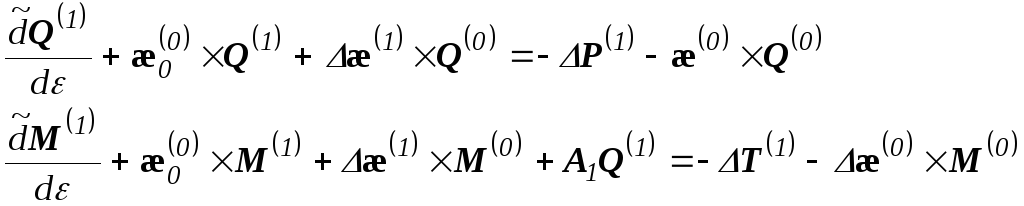
Для следящих нагрузок .

38