Строительная механика машин

Здесь [s₁; s₂], [s₃; s₄] – интервалы действия q и ; s₅, s₆ – точки приложения сосредоточенных внешних нагрузок P и T.

Система уравнений (1.5), (1.6) не является полной, так как неизвестен единичный вектор е₁, зависящий от деформации стержня.

Деформированное состояние стержня будет определяться последовательными углами поворота сечения относительно начального положения вокруг осей 1, 3, 2 ₁, ₃, ₂ и соответствующими матрицами перехода . Помимо этого деформированное состояние описывается вектором кривизны æ.

Уравнения связи момента M с вектором кривизны æ

Рассмотрим элемент стержня в деформированном состоянии в связанной системе координат (рис.). Обозначим {e_i⁽¹⁾} - базис, связанный с естественными осями, {e_i} – базис, связанный с главными осями инерции сечения, ₁₀ – угол между естественными и главными осями.

Радиус кривизны  направлен по главной нормали, а вектор радиуса кривизны по бинормали естественных осей.

В плоскостях, проходящих через главные оси сечения, проекция осевой линии имеет кривизны æ₂, æ₃, которые являются проекциями вектора кривизны æ пространственной осевой линии, кручение осевой линии стержня характеризуется компонентой æ₁.

Считем, что связь M и æ линейная (физически линейная теория), т.е. изгибающие моменты М₂, М₃ и крутящий момент М₁ пропорциональны изменениям кривизн æ₂, æ₃ и кручения æ₁ осевой линии стержня. Получим три уравнения:

Здесь æ₂₀, æ₃₀ , æ₁₀ - кривизны и кручение в недеформированном (естественном) состоянии стержня.

Или в векторной форме

Здесь

Вектор не равен вектору , который характеризует естественное (недеформированное) состояние стержня:

Если оси x₂ и x₃ – главные оси инерции прямоугольного сечения

Перейдем в векторном уравнении () к неподвижным декартовым осям (базис ).

Чтобы найти приращения кривизн , входящих в уравнения (), надо считать, что вектор при деформации стержня остается без изменения в связанной системе координат (в базисе {e_i}), что имеет место, если его проекции в этой системе координат не меняются. В этом случае

Получим уравнение () в декартовых осях в базисе {i_j}:

Так как , то

Уравнение ()

устанавливает связь между проекциями вектора М_x в декартовых осях и приращениями кривизн в связанных осях, где .

Уравнение, связывающее векторы и .

Уравнение связи вектора кривизны и вектора углов поворота координатных осей

имеет вид:

Другие формы уравнения () удобные при преобразованиях:

В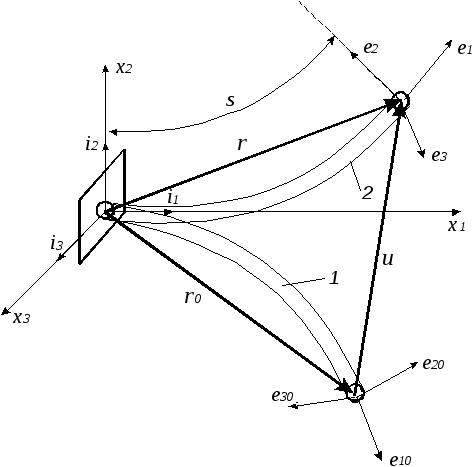екторное уравнение перемещений точек осевой линии

Из курса дифференциальной геометрии известно:

Найдем производную вектора перемещения точки осевой линии:

Считаем, что в недеформированном состоянии вектор кривизны известен и известна матрица перехода .

Связь базиса в ненагруженном (естественном) состоянии с декартовым базисом:

Связь базиса в нагруженном (деформированном) состоянии с базисом естественного состояния:

Тогда, связь базиса в нагруженном (деформированном) состоянии с декартовым:

Исключаем из уравнения ()

Получаем уравнение для определения перемещений точек осевой линии, для случая, когда вектор перемещения задан через базис деформированного состояния

Исключаем из уравнения ()

Получаем уравнение для определения перемещений точек осевой линии, для случая, когда вектор перемещения задан через базис естественного состояния

Получим уравнение перемещений точек осевой линии стержня для вектора u в декартовых осях в базисе {i_j}, воспользовавшись матрицей преобразования L⁰ базиса { i_j} к базису {e_i}.

Учтем, что , , следовательно

Тогда

Уравнение () позволяет определить компоненты их вектора перемещений и в декартовой системе координат (абсолютные перемещения).

Если стержень в естественном состоянии был прямолинейным, то в этом случае L⁰=E и уравнение () принимает вид:

Или

Полная система векторных уравнений равновесия пространственно-криволинейного стержня:

или

Пять векторных уравнений относительно пяти неизвестных векторов .

Уравнения (1),(2) инвариантны относительно систем координат, в этих уравнениях можно представить векторы как в неподвижной системе координат

,

так и в подвижной системе координат

.

Уравнения (3),(4),(5) справедливы только в связанных осях (в базисе {е_j}). Уравнение (5’) справедливо только в декартовой системе координат (в базисе {i_j}).

Краевые условия. Однородные и неоднородные краевые условия

Всего имеем двенадцать краевых условий, по шесть на каждом конце стержня.

Для консоли краевые условия, записанные в векторной форме:

При s=0 u=0; =0 – кинематические краевые условия.

При s=l Q=P; =T - силовые краевые условия.

Для шарнирно-опертого стержня имеем неоднородные (смешанные) краевые условия:

При s=0 u=0 =0.

При s=l u₂=0; u₃=0; Q₁=P; =0.

Представление внешних нагрузок

Мертвые нагрузки:

(например – сила тяжести)

Перейдем к подвижной системе координат:

Или в векторной форме , здесь - матрица перехода от декартова базиса к базису связанных осей.

Следящие нагрузки:

Перейдем к декартовой системе координат:

Или в векторной форме

Приращения векторов при изменении связанных осей. Приращения внешних нагрузок.

При выводе уравнений равновесия необходимо определять приращения векторов внешних и внутренних сил и моментов, и векторов, характеризующих положение и форму стержня в пространстве. На рис. показано два положения базиса, связанного с осевой линией стержня: (1) - начальное и (2) - конечное. При перемещении базиса {е_i0} в пространстве вектор а₀ меняется как по направлению, так и по модулю. При выводе уравнений равновесия в связанной системе координат необходимо знать изменения проекций вектора, т. е. , где а_i0 - проекции вектора а₀ в исходной системе координат (базис {е_i0}); а_i - проекции вектора а в новом положении координат (базис {е_i}). Необходимо также знать приращение вектора

, где .

Введем вектор , здесь a_i0 – компоненты a₀ в базисе {e_i0}.

Тогда приращение вектора в связанных осях

.

Пример. Найдем приращение нагрузки при потере устойчивости стержня.

При исследовании статической устойчивости стержней требуется определять приращения внешней нагрузки, которая, при потере стержнем устойчивости остается по модулю неизменной, а изменяет только свое направление по отношению к подвижной (связанной) системе координат, т. е. . В этом случае приращения компонент вектора P вызваны только изменением направления вектора P₀ по отношению к связанной системе координат при переходе в новое состояние. Вектор P, представленный в базисе {e_i} через компоненты в базисе {e_i0}, равен , . Тогда

Для малых углов ₁, ₂, ₃ матрица перехода

Так как P_i0 – известны, а _i – неизвестны, удобно использовать представление приращения нагрузки в виде

При численном решении уравнений равновесия удобно приращение векторов внешних нагрузок представить линейно зависящими от u и  (при малых отклонениях осевой линии от ее естественного состояния)

Здесь C⁽ⁱ⁾, B⁽ⁱ⁾ –известные матрицы.

Приведение уравнений равновесия к безразмерной форме записи

Введем безразмерные величины.

Безразмерная криволинейная координата

, где , l – длина стержня.

Безразмерная жесткость ,

- значение изгибной жесткости в начале координат.

Безразмерная кривизна .

Безразмерные нагрузки (внутренние и внешние):

Безразмерная -функция .

Тогда, опуская знак тильды, получим систему векторных уравнений равновесия в безразмерных координатах:

или

Здесь

Векторные уравнения равновесия в связанной системе координат

Чтобы получить уравнения равновесия в проекциях на подвижные координатные оси, необходимо представить векторы в базисе {е_i} (например, связанном с главными осями инерции сечения). При этом надо иметь в виду, что от  зависят не только проекции соответствующих векторов, но и векторы базиса е_i(). Перейдем к локальным производным, учитывая, что

Тогда

Частные случаи уравнений в связанной системе координат

Рассмотрим стержень постоянного круглого сечения (A_ii()=const, A₂₂=A₃₃), прямолинейный в естественном состоянии (), на свободном конце стержня приложены следящие нагрузки P и T, их учтем в граничных условиях.

Раскрывая векторные произведения, получим:

Тогда в проекциях на направления базисных векторов e_i уравнения примут вид:

Подставим (3) в (2):

(*)

Так как , то . Из граничных условий имеем , тогда . Таким образом, крутящий момент и кручение постоянны по всей длине и не зависят от внешней нагрузки.

Пусть внешняя нагрузка P=0, момент – следящий, т.е. Ti()=const.

Граничные условия:

при =0 u_i=0; Q_i=0;

при =1 M_i= T_i; Q_i=0;

Из уравнений (*) получаем

Следовательно

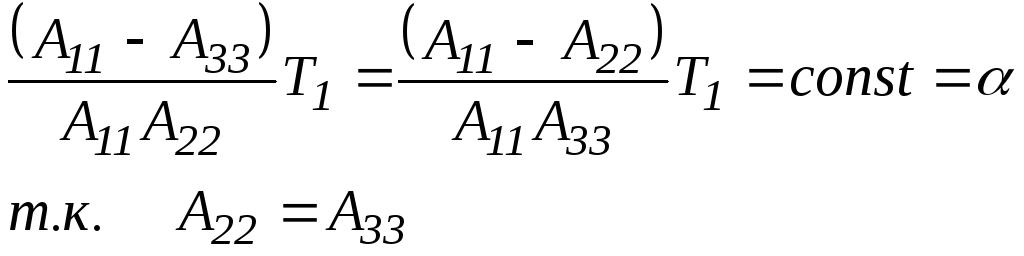
Тогда

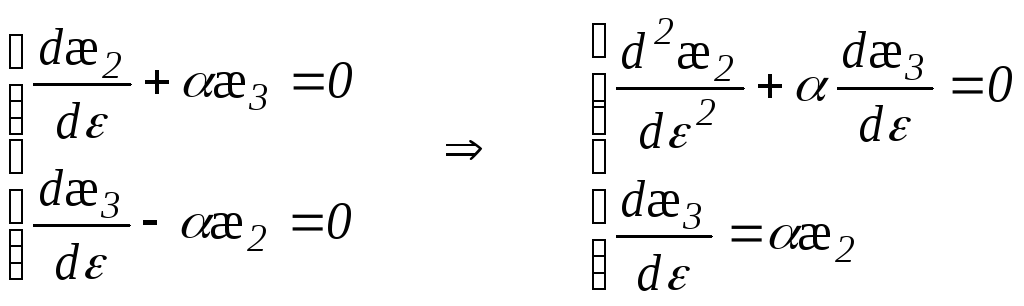
Получаем линейное однородное дифференциальное уравнение второго порядка:

Решение уравнения:

Получаем

Константы интегрирования находим из граничных условий при =1:

По правилу Крамера:

Таким образом, определен вектор кривизны .

Так как стержень в естественном состоянии прямолинейный , тогда из уравнения (4), получаем

Или

В проекциях на связанные оси

Система может быть решена одним из численных методов при граничных условиях: =0 _i=0 (жесткая заделка).

Для определения перемещений точек осевой линии воспользуемся уравнением () в безразмерной форме.

Так как стержень в естественном состоянии был прямолинейным, базисы {i_j} и {e_j0} совпадают, поэтому , l_1i – элементы матрицы перехода L:

Тогда

Граничные условия =0 u_xi=0 (жесткая заделка).

Уравнения равновесия в декартовой системе координат

Запишем все векторы в базисе {i_j}:

В декартовой системе координат полная производная совпадает с локальной, тогда, учтя формулы преобразования векторов при переходе от базиса {e_j} к базису {i_j} , получим уравнения

Все входящие в эти уравнения векторы, есть векторы в базисе {i_j}.

Уравнения равновесия при малых углах поворота и перемещениях

Рассмотрим уравнения в связанных осях

Пусть компоненты малы, причем внешние нагрузки могут быть любыми и компоненты векторов Q и М считать малыми нельзя.

Представим

Здесь - соответствуют известным нагрузкам, действующим на абсолютно твердый (не деформируемый) стержень. - приращения внешних нагрузок, зависящие от перемещений и углов . Тогда их можно представить

- известные матрицы.

Рассмотрим уравнение (1,2), представив ,

Если компоненты вектора можно считать малыми по сравнению с компонентами вектора , то произведения можно приближенно положить равными нулю. В этом случае получаем при решении уравнений приближенные значения векторов Q, М. Следует заметить, что пренебречь произведением векторов можно только в том случае, когда . Если же , то для линеаризации уравнений равновесия надо использовать начальное напряженное состояние стержня, вызванное силами, которые не изменяют его прямолинейной формы (осевое усилие Q₁₀ и крутящий момент M₁₀: ).

При малых углах поворота связных осей

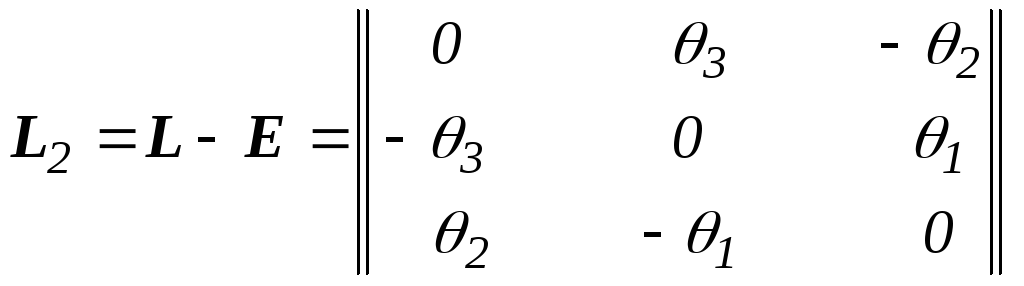
Так как компоненты _i малы, то ;

Компоненты L: . При малых перемещениях u .

При этих допущениях все векторы, входящие в систему, будут иметь приближенные значения, обозначим их и т.д.