Строительная механика машин

Лекция №1

Строительная механика машин –

один из разделов механики твердого деформируемого тела.

Рассматриваются расчеты на прочность, жесткость, устойчивость в более сложной постановке, чем в «Сопротивлении материалов». Расчетные элементы – криволинейные стержни, тонкостенные стержни, пластины, оболочки. Современные расчетные методы, как аналитические, так и численные, реализация их в программных пакетах Maple, MatLab, FlexPDE и др.

5, 6 семестры – механика стержней,

7, 8 семестры – теория пластин и оболочек.

Литература (5 семестр): В.А. Светлицкий «Механика стержней» т.1, 1987г.;

В.И. Феодосьев «Сопротивление материалов» (ликбез).

МЕХАНИКА СТЕРЖНЕЙ

Теория пространственно-криволинейных стержней

Пространственно-криволинейные упругие элементы, сводящиеся к расчетной модели стержня, являются составной частью многих приборов, механизмов, конструкций.

Например, цилиндрические или конические пружины

К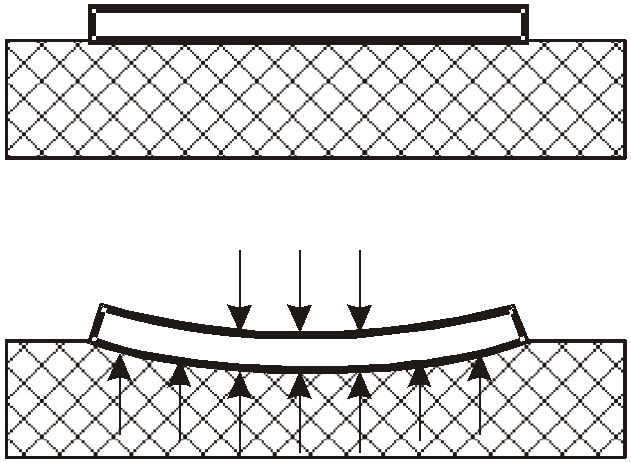роме того, будут рассмотрены гибкие стержни, которые до нагружения имели плоскую криволинейную или прямолинейную форму. Такие стержни после нагружения приобретают значительные искривления осевой линии, хотя деформации остаются в пределах закона Гука. Особый интерес имеют задачи о взаимодействии стержней с потоком газа или жидкости.

Прямолинейные гибкие стержни являются частным случаем криволинейных стержней. Например, задача о стержне, лежащем на упругом основании, в этом случае со стороны основания на стержень действуют контактные силы.

Основные определения и допущения механики гибких стержней

Стержень – тело, размеры поперечного сечения которого малы по сравнению с длиной и радиусом кривизны осевой линии.

Осевая линия – геометрическое место центров тяжести поперечных сечений. Различают осевую линию ненагруженного стержня и осевую линию нагруженного стержня – «упругую» осевую линию.

Особенность гибких стержней – осевая линия нагруженного стержня сильно отличается от осевой линии естественного состояния, но деформации остаются в пределах действия закона Гука. Т.е. задача является физически линейной, а геометрически нелинейной.

Геометрическая нелинейность приводит к тому, что перестают быть справедливыми принцип суперпозиции (независимости действия сил) и принцип неизменности начальных параметров (перемещения, возникающие при деформации, столь малы, что форма и размеры стержня остаются неизменными).

Однако справедливы следующие допущения:

1. Материал стержня изотропный и подчиняется закону Гука, т.е. _max<_п (физически линейная теория).

2. Поперечные сечения нормальные и плоские до деформации остаются плоскими и перпендикулярными осевой линии и после деформации (гипотеза плоских сечений Бернулли).

3. Осевая линия считается нерастяжимой.

4. Принцип Сен-Венана: на достаточном удалении от места приложения нагрузки напряженное состояние не зависит от особенностей приложения внешних сил (а только от главного вектора и главного момента внешней нагрузки).

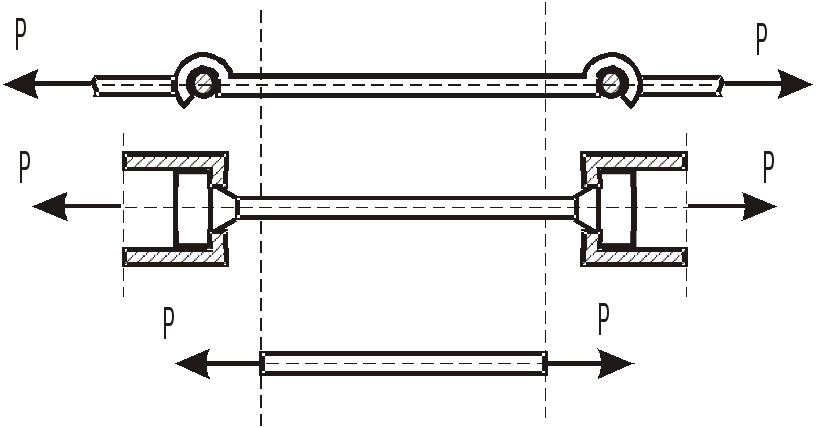
Особенности нагрузок

Н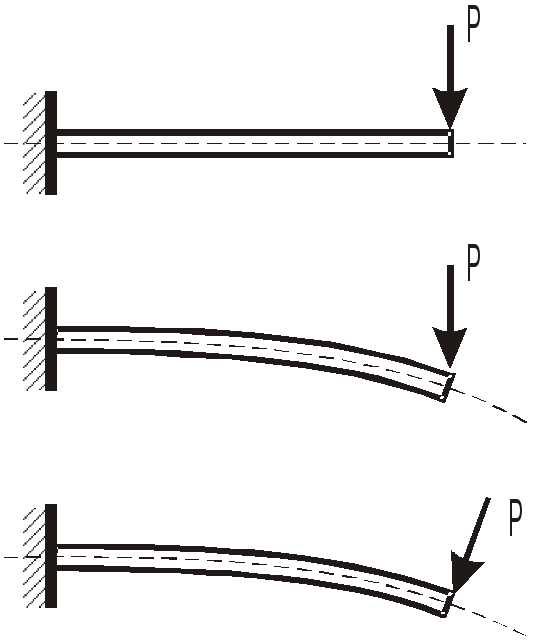агружение статическое, т.е. нагрузки нарастают постепенно. Внешние силы могут изменятся по направлению.

«Мертвые нагрузки» сохраняют при деформации системы свое направление.

Следящая нагрузка в процессе деформации сохраняет свое направление по отношению к стержню, например неизменные углы с подвижными осями координат.

Н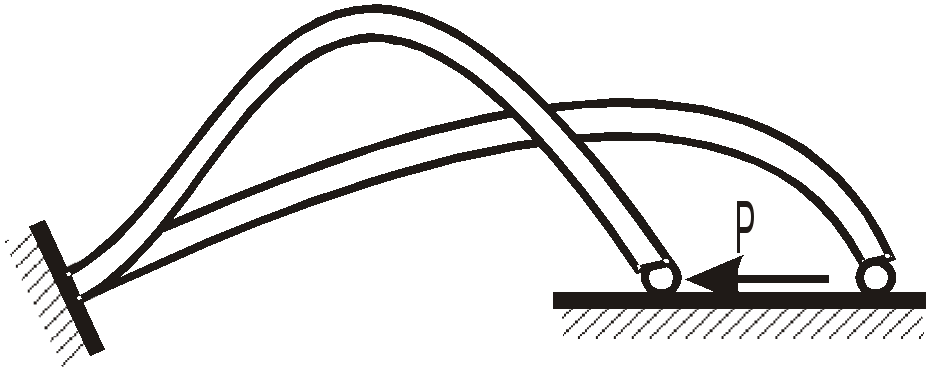еобходимо также учитывать изменение краевых условий, например, перемещение шарнира.

Системы координат в механике гибких стержней

Для исследования условий равновесия гибкого стержня понадобится рассмотрение двух систем координат:

Неподвижная система координат x₁, x₂, x₃ с базисом i₁, i₂, i₃;

Подвижная система координат жестко связанная с осевой линией стержня с базисом е₁, е₂, е₃. Начало подвижной системы координат помещаем в центр тяжести сечения, ось направляем по касательной к осевой линии, оси могут быть направлены по главным осям инерции сечения. Базисные векторы е₁, е₂, е₃ изменяют свое направление при переходе в другую точку пространства.

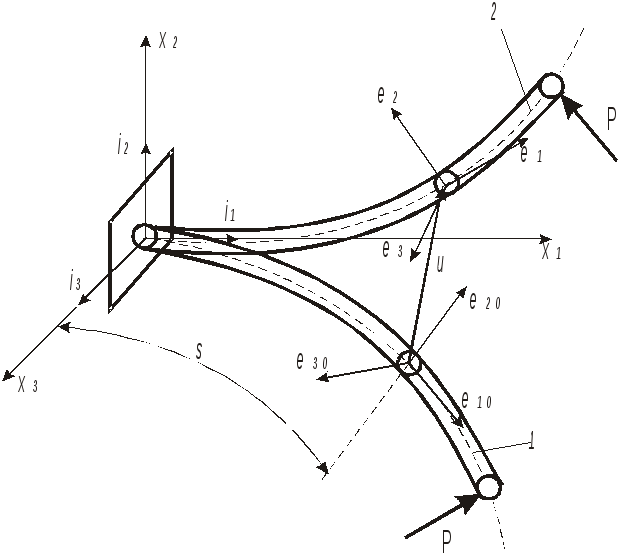
положение 1 – до деформации (естественное состояние);

положение 2 – после деформации

- базис, связанный с сечением в естественном состоянии;

- базис, связанный с тем же сечением в деформированном состоянии.

s – криволинейная координата сечения (длина дуги осевой линии, отсчитываемая от начала неподвижной системы координат)

u – вектор перемещения сечения;

Вектор перемещения может быть представлен через базисные векторы:

Лекция №2

Преобразование базисных векторов при переходе от одной системы координат к другой. Матрица перехода.

Пусть

- базис, связанный с сечением в естественном состоянии;

- базис, связанный с тем же сечением в деформированном состоянии.

Можно разложить e_i по векторам базиса естественного состояния:

,

здесь l_ij –проекции базисных векторов e_i на направления, определяемые векторами e_i0.

Матрица перехода от базиса к базису

, тогда можно записать .

Обратное преобразование

Или, более компактно,

При обратном преобразовании

Определим матрицы перехода при произвольном смещении и повороте тройки базисных векторов.

При поступательном смещении координатных осей базисные векторы совпадают с исходными.

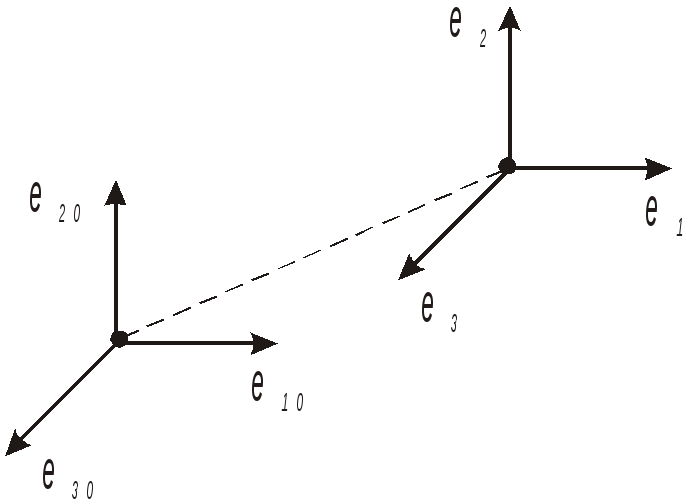
Произвольный поворот можно представить, как три последовательных поворота.

Первый поворот – вокруг оси, совпадающей по направлению с e₁₀, на положительный угол ₁ (углы положительные – против хода часовой стрелки).

Получим

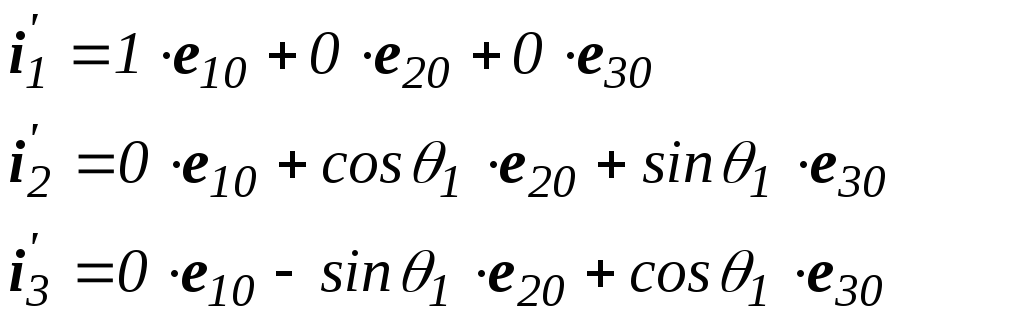
Матрица перехода

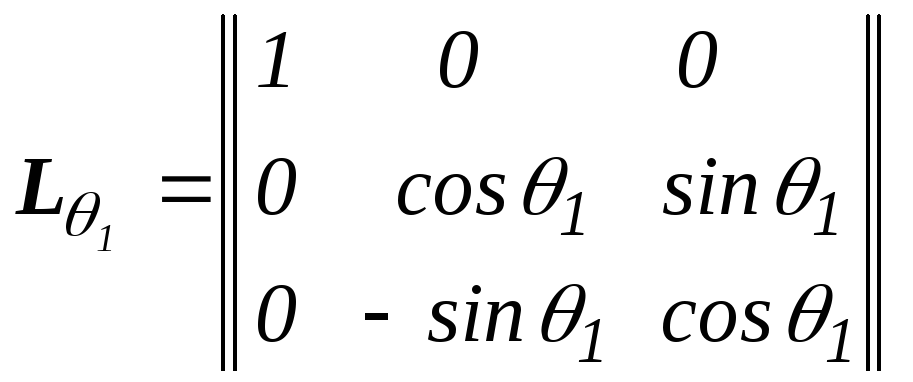
Элементы матрицы можно рассматривать как направляющие cos между векторами e_i0 и i_i’.

Второй поворот – вокруг оси, совпадающей по направлению с i₃’, на положительный угол ₃.

Получим

Матрица перехода

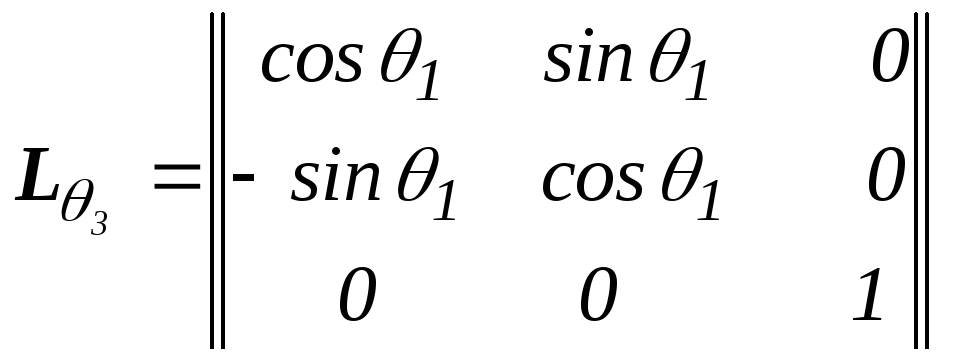
Третий поворот – вокруг оси, совпадающей по направлению с i₂”, на положительный угол ₂.

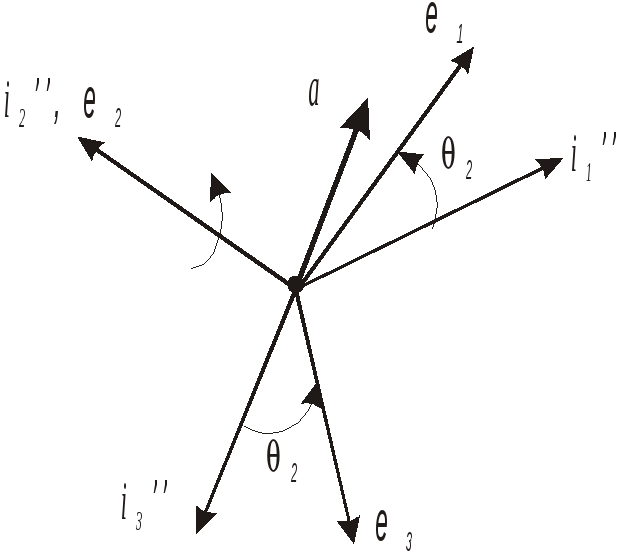
Получим

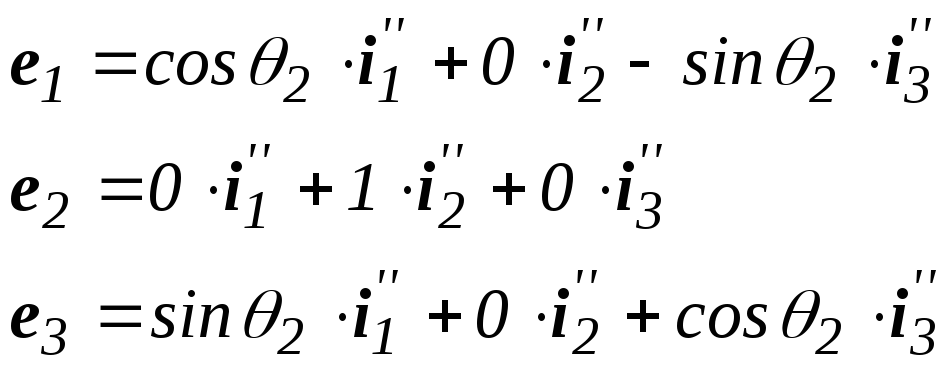
Матрица перехода

Компоненты произвольного вектора при каждом из поворотов преобразуются

В итоге ,

матрица перехода

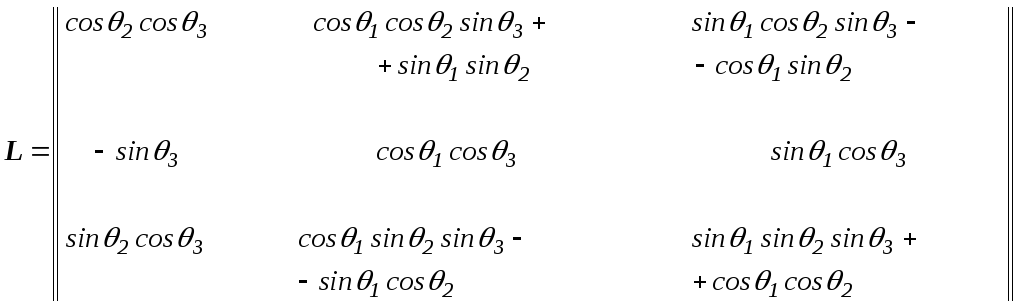
Связь между компонентами вектора a в разных базисах , где - компоненты вектора a в базисе , где - компоненты вектора a в базисе . Тогда .

При малых углах , тогда матрица перехода принимает вид

Или , где .

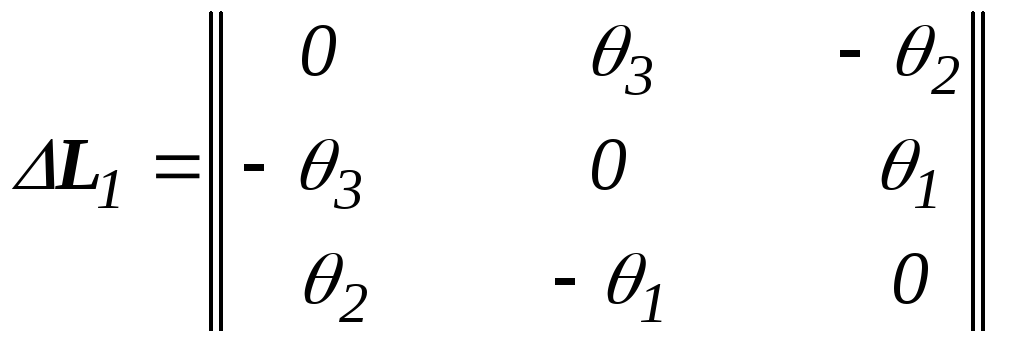Свойства матрицы перехода

Матрица перехода – ортогональная матрица, для ортогональной матрицы

.

Элементы матрицы перехода удовлетворяют условиям (т.к. ):

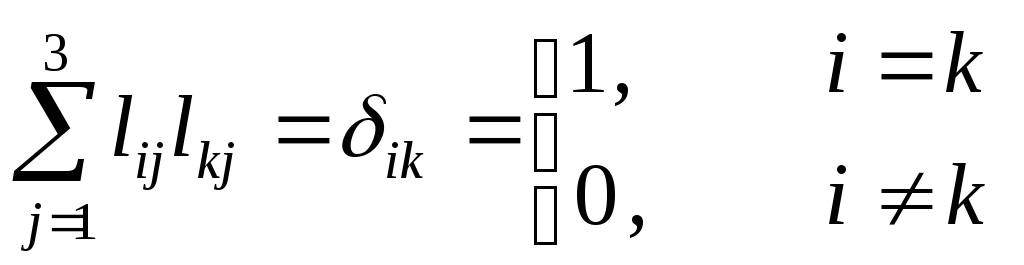, (- символ Кронекера)

т.е.

Так как , получаем еще шесть дополнительных условий

Рассмотрим матрицу преобразования базиса к базису . Матрица перехода , где - матрица перехода от базиса к базису - это матрица с известными компонентами, характеризующими пространственную форму осевой линии стержня в ненагруженном естественном состоянии. Для стержня прямолинейного в естественном состоянии .

Лекция №3

Основные положения дифференциальной геометрии пространственных кривых

Производные радиуса-вектора

Рассмотрим плоскую кривую, радиус вектор r(s) , приращение радиуса вектора .

Производная радиуса-вектора:

,

т.е. производная вектор-функции r(s) по ее скалярному аргументу s есть вектор, направленный по касательной к кривой, причем

Тогда .

Вторая производная радиуса-вектора: .

Скалярное произведение

Продифференцируем скалярное произведение:

.

Тогда

Получаем:

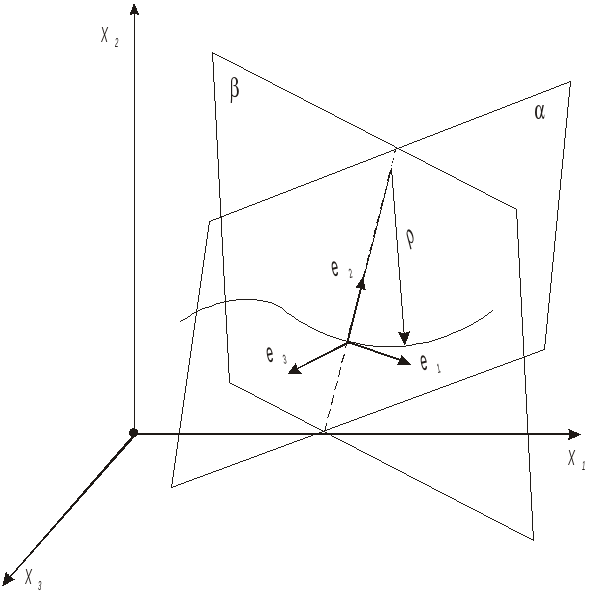
Рассмотрим пространственную кривую.

Естественные оси: касательная (е₁), соприкасающаяся плоскость (), главная нормаль (е₂) лежит в соприкасающейся плоскости, бинормаль (е₃) лежит в плоскости  (плоскость  – плоскость нормальная к е₁). Вторая производная радиуса-вектора, как и для плоской кривой, равна

,

Причем вектор второй производной лежит в соприкасающейся плоскости,  – радиус кривизны пространственной кривой есть радиус соприкасающейся окружности, лежащей в соприкасающейся плоскости .

Производные базисных векторов

Т.к. производные базисных векторов есть вектора, представим их в виде разложения по базисным векторам , причем е₁ направлен по касательной к пространственной кривой (к осевой линии стержня):

Умножим скалярно на e_k

Скалярное произведение базисных векторов .

Продифференцируем скалярное произведение:

Получаем

Т.е. матрица (матрица кривизны) кососимметрична, имеет три независимых компонента

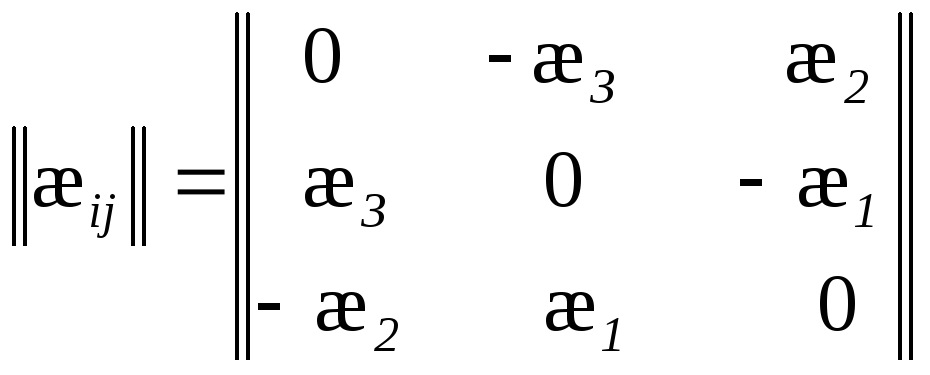
и характеризует геометрию пространственной кривой (осевой линии стержня).

Можно ввести вектор кривизны , тогда производные базисных векторов можно представить в виде

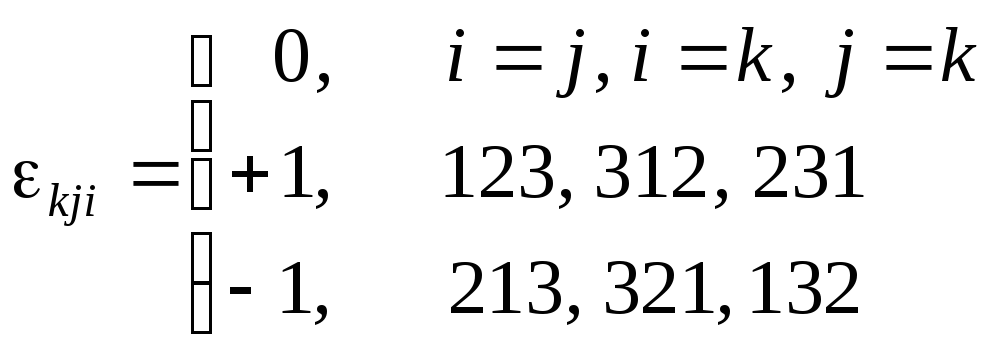- символы Леви-Чивита

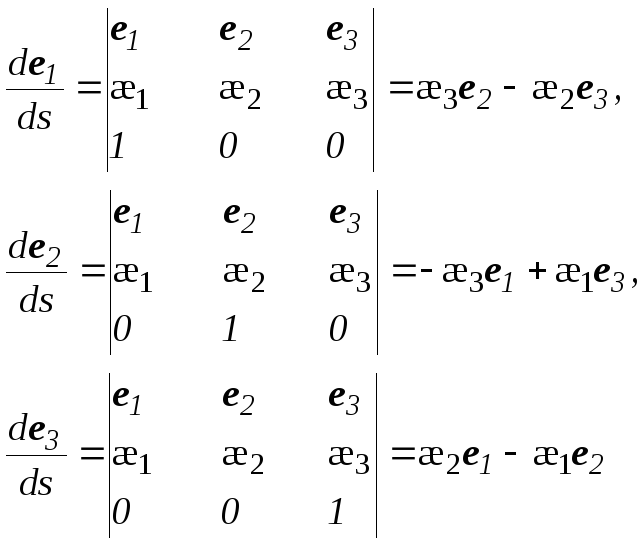
Геометрический смысл компонент вектора кривизны

Рассмотрим естественные связанные оси (e₂ и e₃ направлены по главной нормали и бинормали). В этом случае вектор кривизны называется вектором Дарбу

.

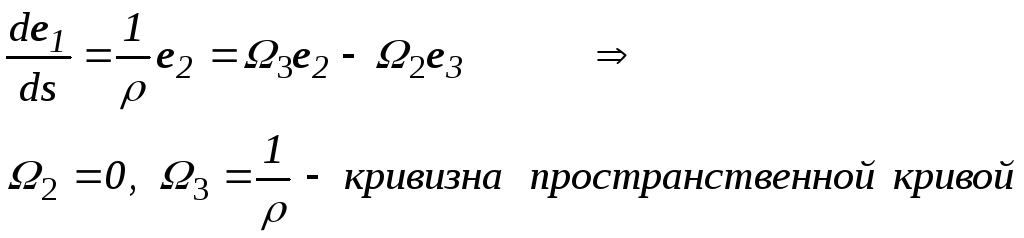
Тогда производные базисных векторов для естественных связанных осей

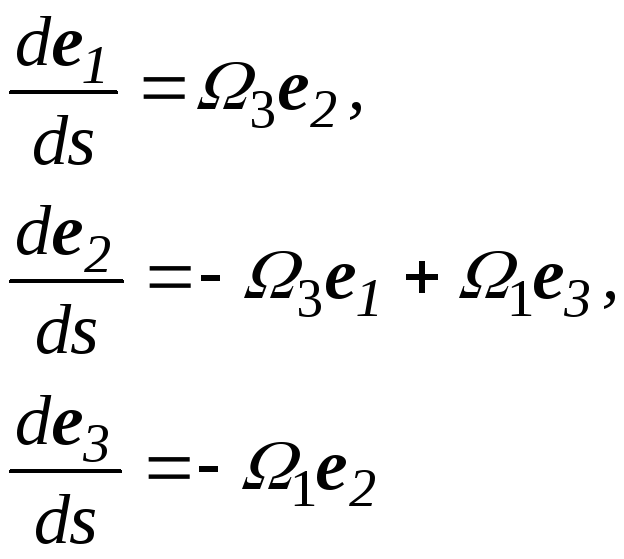
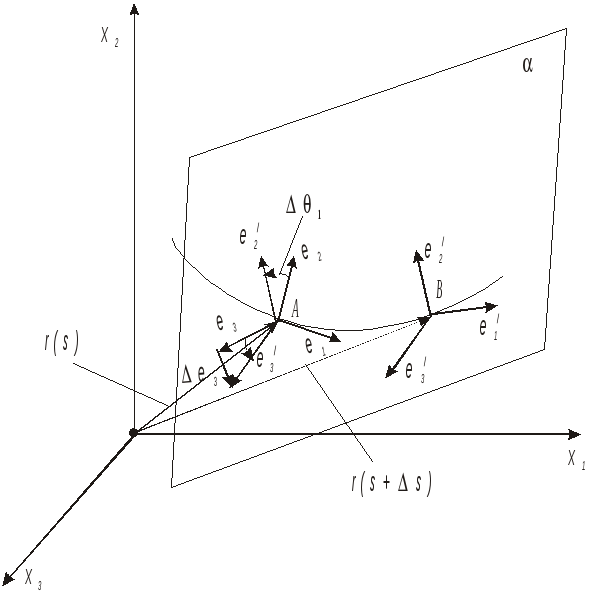
- формулы Сере-Френе

Геометрический смысл компоненты

Тогда

характеризует кручение кривой – меру уклонения кривой от соприкасающейся плоскости.

Т.о. вектор Дарбу характеризует вращение естественных осей при движении точки по кривой.

, следовательно, вектор Дарбу лежит в плоскости , перпендикулярной соприкасающейся плоскости .

Р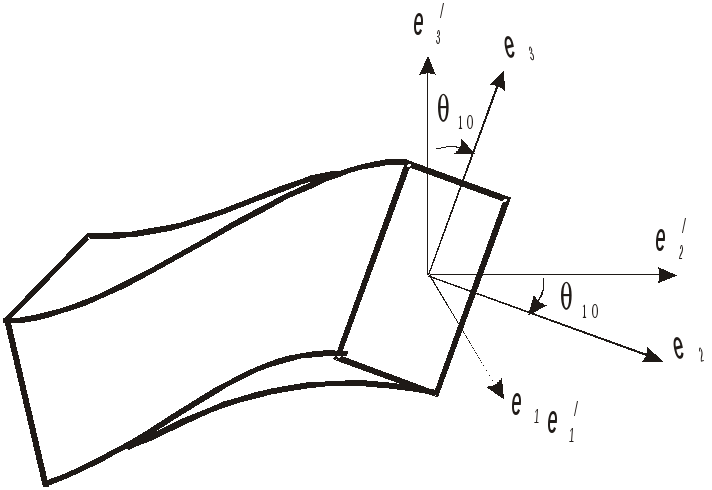ассмотрим произвольный базис. Вектор кривизны характеризует поворот произвольного базиса при движении точки вдоль пространственной кривой (например, е₂ и е₃ направлены по главным осям инерции сечения). Главные оси повернуты относительно естественных осей на угол .

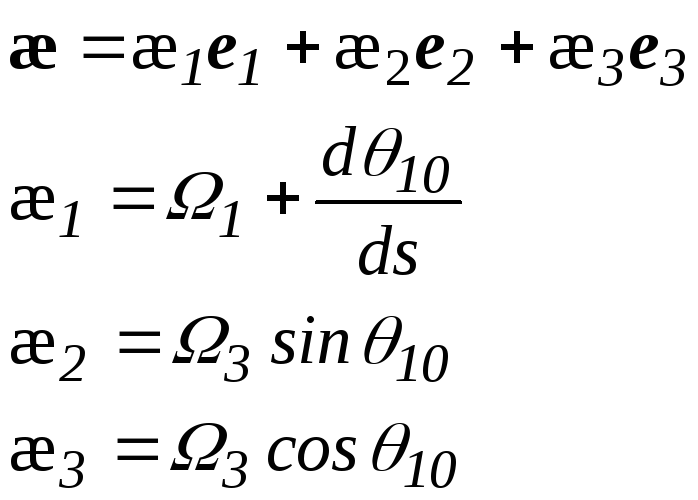
Компонента ₁ представляет собой сумму двух величин – кручения осевой линии стержня ₁ и скорости вращения главных осей относительно естественных осей . Угол может быть не связан с деформацией стержня, как, например, для естественно закрученного стержня – сверла.

Производная вектора в связанной системе координат.

Удобно представить

Для естественных координатных осей

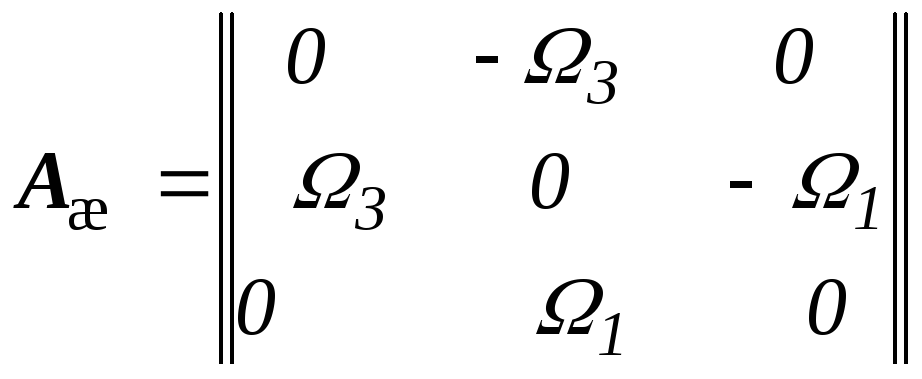
Тогда .

Лекция №4

Элементарные обобщенные функции. Представление нагрузок.

Введем в рассмотрение функцию (z), имеющую max при z=0 и быстро убывающую с ростом z, причем . Таким условиям удовлетворяет, в частности, функция

.

При неограниченном увеличении m получаем функцию, называемую -функция Дирака:

Качественное поведение функций и показано на рис.

Размерность -функции .

При переходе к безразмерным переменным  вводится в рассмотрение безразмерная -функция . Покажем, что справедливо равенство

,

где a – размерный параметр

Рассмотрим интеграл

При a>0

При a<0

Таким образом функция удовлетворяет всем свойствам -функции.

Производные -функции вводятся следующим образом:

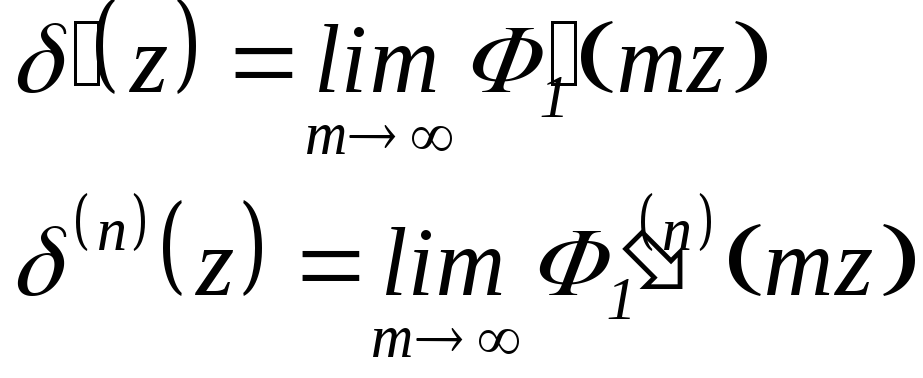
Производная от безразмерной -функции

Смещенная -функция

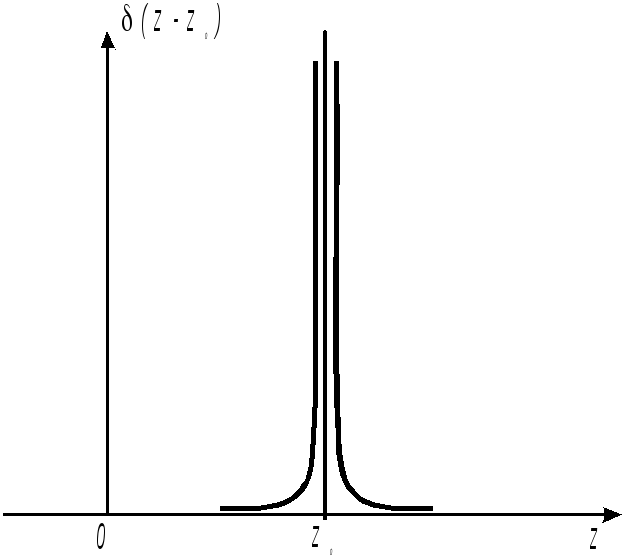
Введем в рассмотрение функцию Хевисайда, связанную с -функцией условием

Производная функции Хевисайда

Интеграл от функции Хевисайда

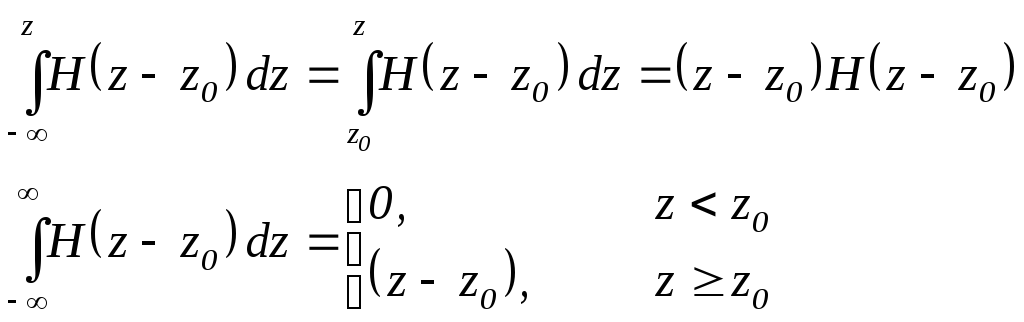
Фильтрующие свойства -функции.

Пусть r –малая величина, тогда непрерывная функция f(z) на интервале (z₀-r; z₀+r) имеет практически постоянное значение f(z)=f(z₀).

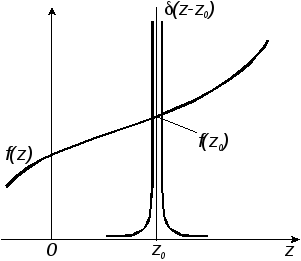
Учитывая свойства -функции, имеем:

Для интеграла с переменным верхним пределом

Если подинтегральное выражение зависит от производной

В общем случае

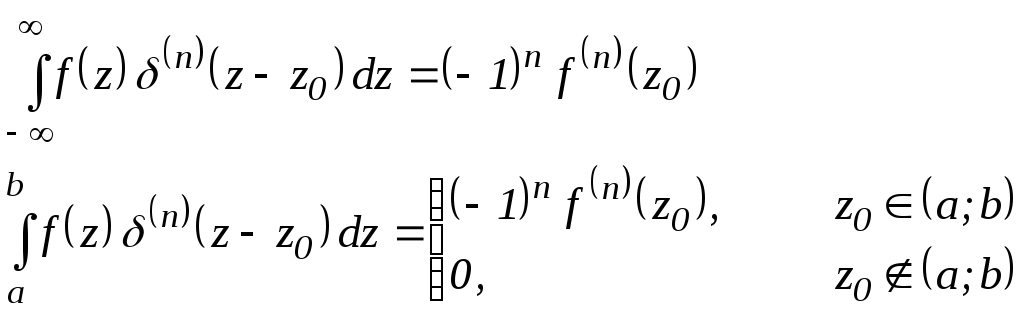
При переменном верхнем пределе

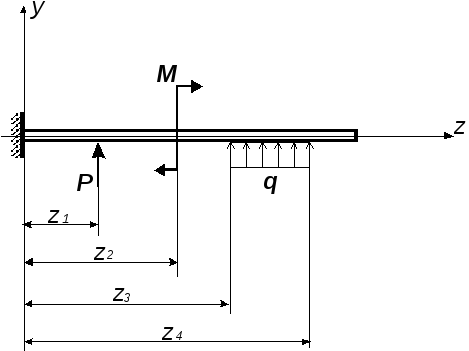
Использование обобщенных функций для представления нагрузок, действующих на стержень.

Благодаря указанным свойствам обобщенные функции Н(z – z₀) и  (z – z₀) оказались очень удобными для аналитического описания сосредоточенных и кусочно распределенных нагрузок, действующих на стержень. При этом интенсивность нагрузки может быть представлена непрерывной и дифференцируемой функцией во всей области, занимаемой объектом.

1. На стержень действует сосредоточенная поперечная сила P в точке z = z₁. Интенсивность нагрузки

.

2. На стержень действует сосредоточенный изгибающий момент М в точке z = z₂. Тогда

3. На стержень действует распределенная нагрузка от точки z = z₃, до точки z = z₄. В этом случае

Лекция №5

Векторные уравнения равновесия стержня

Рассмотрим элемент стержня длиной ds, находящийся в равновесии. Действующие на него силы: Q=Q₁e₁+Q₂e₂+Q₃e₃ — вектор внутренних усилий, где Q₁ — осевая сила, Q₂ и Q₃ — перерезывающие силы; M=M₁e₁+M₂e₂+М₃е₃ — вектор внутренних моментов, где M₁ — крутящий момент, М₂ и М₃ — изгибающие моменты; q₁, q₂, q₃ — проекции вектора q распределенной (внешней) нагрузки на связанные оси; ₁, ₂, ₃ — проекции вектора  распределенного (внешнего) момента на связанные оси. Направления осей, определяемые единичными векторами е₂ и е₃, совпадают с направлениями главных осей сечения стержня. Элемент находится в равновесии; следовательно, сумма всех сил и сумма моментов равны нулю, что дает два векторных уравнения:

Здесь момент силы представлен через векторное произведение вектора силы Q на радиус-вектор точки приложения силы.

Или

В векторной форме записи уравнения инвариантны по отношению к любой системе координат. Для перехода от уравнений (1.3), (1.4) к уравнениям, записанным через компоненты векторов в каком-либо базисе, необходимо представить векторы в виде разложения по векторам данного базиса. В уравнениях (1.3), (1.4) неизвестными являются векторы Q, М и e₁; известными — распределенные нагрузки q и , сосредоточенные силы и моменты, приложенные к стержню (см. рис. 1.1), и условия закрепления стержня. Сосредоточенные силы и моменты можно ввести в уравнения (1.3) и (1.4), воспользовавшись -функцией Дирака. Распределенные силы q и распределенные моменты , которые действуют не по всей длине, а лишь на части стержня могут быть представлены с использованием функции Хевисайда.