4.2. Метод интервалов.

1º. Если дискриминант квадратного трехчлена D > 0илиD = 0, то квадратное неравенствоможно переписать в видеили, гдеx₁иx₂– корни квадратного трехчлена, и использовать для его решения метод интервалов.

2º. Для решения любых алгебраических уравнений

вида (1)или вида (2), гдеx₁, x₂, …, x_n– действительные числа, удовлетворяющие условиюx₁ < x₂ < …< x_n, а k₁, k₂, …, k_n – натуральные числа, применимобобщенный метод интервалов.

Суть его состоит в следующем: на координатной оси отмечают числа x₁, x₂, …, x_n, в промежутке справа отx_nставят знак +,

затем, двигаясь справа налево, при переходе через очередную точку x_iменяют знак, еслиk_i- нечетное число и сохраняют знак, еслиk_i- четное число. Тогда множеством решений неравенства (1) будет объединение промежутков, в каждом из которых поставлен знак +, а множеством решений неравенства (2) будет объединение промежутков, в каждом из которых поставлен знак – .

Замечание.Обобщенный метод интервалов справедлив и для целых рациональных неравенствP(x) > 0 илиQ(x) ≥ 0, и для дробно-рациональных неравенствили, причем последние равносильны неравенствуи системе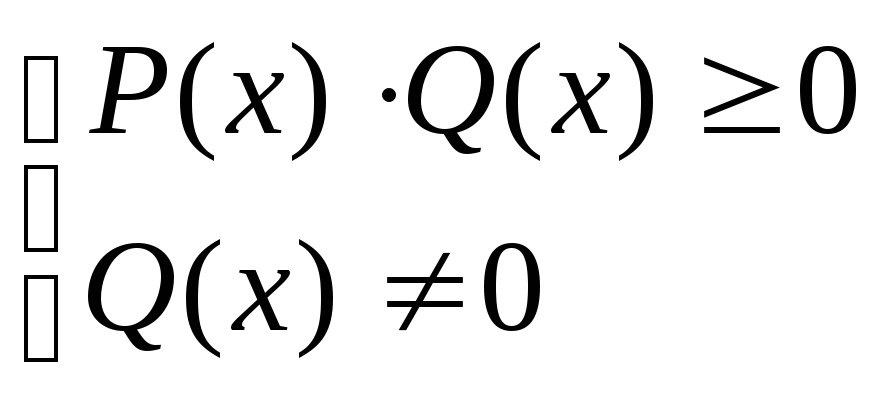соответственно, гдеP(x), Q(x)– некоторые многочлены.

Пример 11. Решить неравенство .

Решение: Находим корни квадратного трехчлена :

Данное неравенство равносильно следующему неравенству:. Применяя метод интервалов к последнему неравенству, получим множество всех решений неравенства – отрезок [-2; 3].

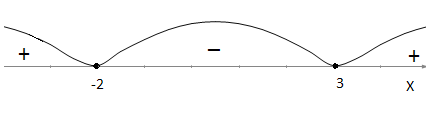
Ответ: .

Пример 12. Решить неравенство .

Решение:

Находим корни числителя и знаменателя:

Указанная система равносильна следующей системе:

Нанесем найденные корни на числовую прямую. В интервалах справа налево расставим знаки плюс и минус.

Множеством всех решений данного неравенства является объединение промежутков, в которых поставлен знак минус.

Ответ: .

Дидактический материал.

Решите неравенства:

1. ; 2.;

3. ; 4..

Решите системы неравенств:

5. ; 6..

Найдите целые решения системы неравенств:

7. 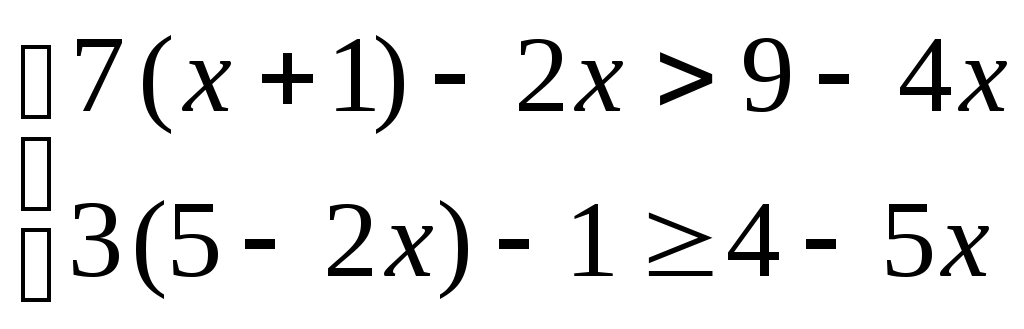; 8..

Решите неравенства:

9. ; 10.; 11.;

12. ; 13.;

14. ; 15.;

16. ; 17.;

18. ; 19.;

20. ; 21.; 22.;

23. ; 24.;

25. ; 26.;

27. ; 28.; 29.;

30. ; 31.; 32..

Тема №5. Неравенства с одной переменной (часть II).

5.1. Неравенства, содержащие знак модуля.

1º. При решении неравенств, содержащих неизвестные под знаком модуля, используется определение модуля, что приводит к рассмотрению двух случаев:

а) f(x) ≥ 0, тогда|f(x)| = f(x);

б) f(x)<0, тогда|f(x)| = -f(x).

2º. При решении неравенств вида|f(x)| < aили|f(x)| > bполезно использовать следующие соотношения:

1. неравенство вида |f(x)| < a(или|f(x)| ≤ a), гдеa > 0, равносильно двойному неравенству–a < f(x) < a (или–a ≤ f(x) ≤ a);

2. неравенство вида |f(x)| > b (или|f(x)| ≥ b), гдеb > 0, равносильно совокупности двух неравенств.

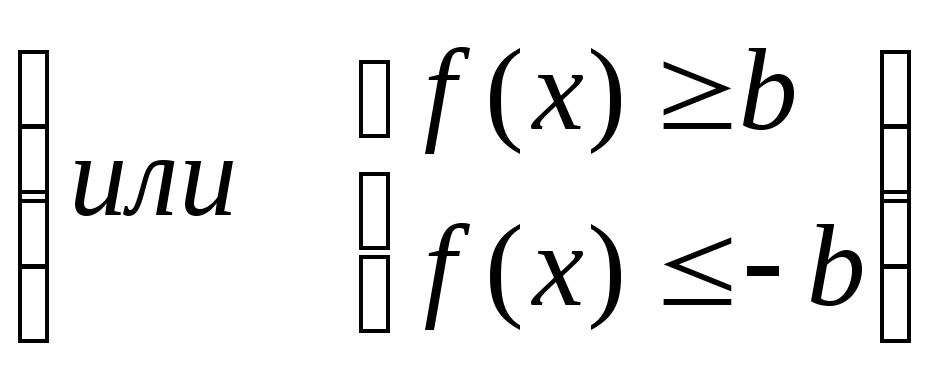3º. Для решения неравенств вида |f(x)| > |g(x)|используют метод возведения в квадрат обеих частей неравенства:

Пример 13. Решить неравенство .

Решение: Возведя обе части неравенства в квадрат, получим неравенство, равносильное данному: . Преобразовав последнее неравенство, получим, откуда находим:x ≤ - 2 , x ≥ 0.

Ответ: .

4º. Для решения неравенств вида часто применяют «метод промежутков». Находят ОДЗ неравенства, затем находят корни совокупности уравнений.

Эти корни разбивают ОДЗ на некоторое число промежутков. На каждом промежутке |f_i(x)|=f_i(x)или |f_i(x)|=-f_i(x), i=1,2,…,n. Поэтому на каждом из них данное неравенство заменяется на другое неравенство, уже не содержащее знаков модуля и равносильное данному неравенству на этом промежутке. Затем решают полученные неравенства (каждое на своем промежутке). Объединение всех найденных решений дает решение исходного неравенства.

Пример 14. Решить неравенство .

Решение:

Решение первой системы: ; второй:; третьей:. Объединяя, получим.