
- •Тема №1. Арифметические вычисления. Проценты.
- •Обыкновенные дроби. Действия над обыкновенными дробями.
- •Дидактический материал.
- •Десятичные дроби. Действия над десятичными дробями.
- •Дидактический материал.
- •Процент. Основные задачи на проценты.
- •Дидактический материал.
- •Тема №2. Уравнения. Модуль числа.
- •Уравнения с одной переменной. Равносильность уравнений.
- •Решение уравнений с одним неизвестным, сводящихся к линейным.
- •Квадратные уравнения.
- •Квадратичная функция, ее график.
- •Уравнения, содержащие переменную под знаком модуля.
- •Дидактический материал.
- •Тема №3. Степени и корни.
- •3.1. Степень с целым показателем.
- •3.2. Арифметический корень. Степень с рациональным показателем.
- •3.3. Формулы сокращенного умножения.
- •4.2. Метод интервалов.
- •Дидактический материал.
- •Тема №5. Неравенства с одной переменной (часть II).
- •5.1. Неравенства, содержащие знак модуля.
- •5.2. Множество значений функции.
- •Дидактический материал.
- •Тема №6. Иррациональные уравнения.
- •Дидактический материал.
- •Тема №7. Показательные уравнения.
- •7.1. Методы решения показательных уравнений.
- •7.2. Классификация показательных уравнений.
- •Дидактический материал.
- •Тема №8. Показательные неравенства.
- •Дидактический материал.
- •Тема №9. Логарифмы.
- •Дидактический материал.
- •Тема №10. Преобразование тригонометрических выражений.
- •Дидактический материал.
- •Тема №11. Тригонометрические уравнения.
- •11.1. Решение простейших тригонометрических уравнений.
- •11.2. Основные методы решения тригонометрических уравнений.
- •11.3. Таблица значений тригонометрических функций.
- •Дидактический материал.
- •12.2.Стереометрия. Многогранники.
- •Дидактический материал.
- •12.3.Стереометрия. Круглые тела, тела вращения.
- •Дидактический материал.
Тема №3. Степени и корни.
3.1. Степень с целым показателем.
1º. Степенью числа а(![]() )с целым показателемnназывается число
)с целым показателемnназывается число![]() ,
определяемое следующим образом:
,
определяемое следующим образом:
1) если n= 0, а≠
0:![]() ;
;
2) если
![]() :
:![]() ;
;
3) если
![]() а≠ 0:
а≠ 0:![]() .
.
При этом число аназываетсяоснованием степени, а числоn–показателем степени. 2º. Степень с целым показателем удовлетворяет следующим свойствам:
![]()
3.2. Арифметический корень. Степень с рациональным показателем.
1º. Арифметическим корнем k-ой
степени (![]() )
из числа а≥ 0 называется неотрицательное
числоb,k-ая
степень которого равна а:
)
из числа а≥ 0 называется неотрицательное
числоb,k-ая
степень которого равна а:
![]()
2º. Замечание. Для любого действительного числа а, любого натурального числаnдействуют правила:
![]() в частности
в частности![]() .
.
3º. Свойства арифметических корней.
Пусть![]() .
Тогда:
.
Тогда:
1)
![]() ; 2)
; 2)![]() ; 3)
; 3)![]() ;
;
4)
![]() ; 5)
; 5)![]() ; 6)
; 6)![]() ;
;
7)
![]() .
.
4º. Степенью числа a
с рациональным показателем ![]() определяется равенством:
определяется равенством:
![]()
![]()
Степень с рациональным показателем обладает теми же свойствами, что и степень с целым показателем.
Пример 7. Упростить выражение:
![]() .
.
Решение. Используя определение степени и ее свойства, получим:

3.3. Формулы сокращенного умножения.
1º. Во всякого рода алгебраических преобразованиях используются формулы сокращенного умножения:
![]() ;
;![]() ;
;
![]() ;
;![]() ;
;
![]() ;
;
![]() ;
;![]() .
.
Так, если а ≥ 0, b≥ 0, то![]() .
.
Или
![]() .
.
Пример 8. Вычислить
![]() .
.
Решение:
![]()
Ответ: 4.
Дидактический материал.
Вычислите:
1.
![]() ; 2.
; 2.![]() ; 3.
; 3.![]() ;
;
4.
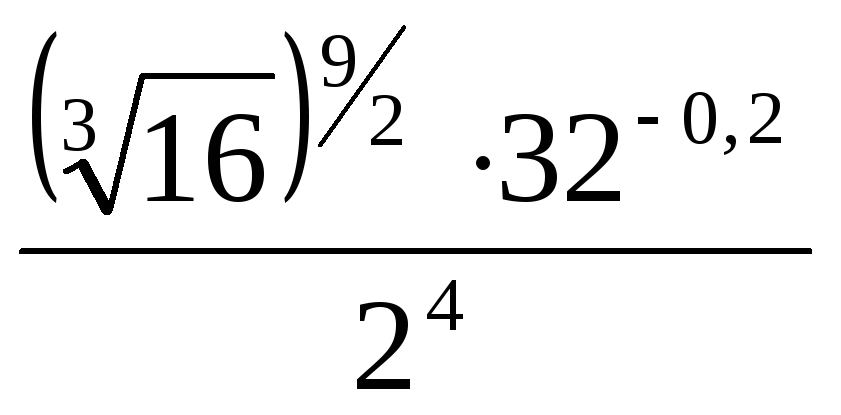 ; 5.
; 5.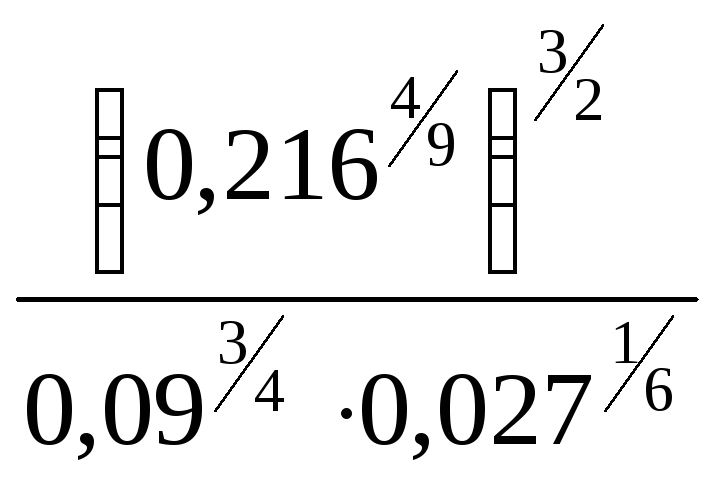 ; 6.
; 6.![]() ;
;
7.
![]() ; 8.
; 8.![]() ;
;
9.
![]() ; 10.
; 10.![]() ;
;
11.
![]() ; 12.
; 12.![]() ;
;
13.
![]() ; 14.
; 14.![]() ; 15.
; 15.![]() .
.
Внесите множители под знак общего корня:
16.
![]() ; 17.
; 17.![]() ; 18.
; 18.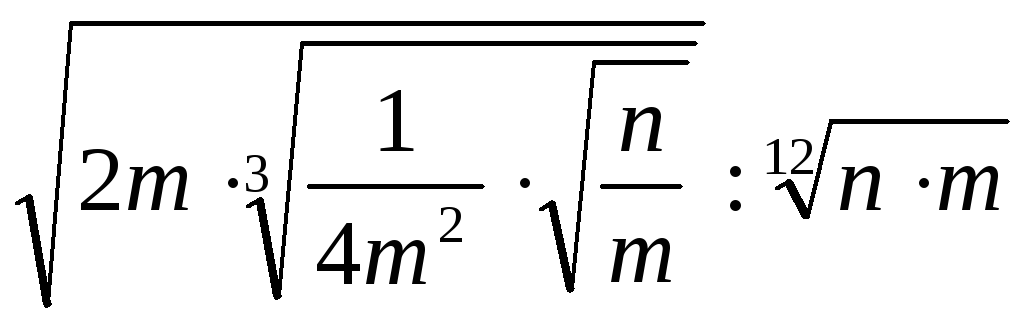 .
.
Упростите выражения:
19.
 ; 20.
; 20.![]() ; 21.
; 21. ;
;
22.
![]() ; 23.
; 23. ;
;
24.
![]() ; 25.
; 25.![]() ;
;
26.
![]() ;
;
27.
![]() .
.
Ответы: 19.![]() ;
20.x+ 4; 21. 0,5; 22. -1;
23.
;
20.x+ 4; 21. 0,5; 22. -1;
23.![]() ;
24. 1; 25. 3; 26.x – y;
;
24. 1; 25. 3; 26.x – y;
27.
![]() .
.
Тема №4.
Неравенства с одной переменной (часть I).
4.1. Решение линейных и квадратных неравенств.
1º. Решить неравенство с одной переменной– значит найти множество значений переменной, при которых это неравенство является верным. Элементы этого множества называютсярешениями неравенства.
Два неравенства, содержащие одну и ту
же переменную, называются равносильными,
если множества решений этих неравенств
совпадают. Равносильность неравенств
обозначается так:![]() .
.
2º. Линейным неравенствомназывается
неравенство вида![]() ,
где
,
где![]() .
.
Если a > 0, то![]() .
.
Если a < 0, то![]() .
.
Пример 9. Решить неравенство, сводящееся к линейному:
![]() .
.
Решение: Раскрыв скобки, получим:
![]() .
.
Ответ:
![]()
3º. Квадратным неравенствомназывается
неравенство вида![]() (или
(или![]() ),
гдеа ≠ 0.
),
гдеа ≠ 0.
При решении квадратного неравенства
![]() в зависимости от знака дискриминанта
в зависимости от знака дискриминанта![]() могут представиться 3 варианта:
могут представиться 3 варианта:
1) Если D < 0, то
график квадратного трехчлена![]() не пересекает осьОхи лежит выше
этой оси приa > 0и ниже ее приa < 0.
В первом случае множество решений
неравенства есть вся числовая прямая,
а во втором – пустое множество.
не пересекает осьОхи лежит выше
этой оси приa > 0и ниже ее приa < 0.
В первом случае множество решений
неравенства есть вся числовая прямая,
а во втором – пустое множество.
2) Если D > 0, то
график квадратного трехчлена пересекает
осьОхв точкахх1их2
(x1 <
x2),
являющихся корнями уравнения![]() .
Эти точки разбивают числовую прямую на
три промежутка(-∞; x1),
(x1; x2),
(x2; +∞).Еслиa > 0, то
решением неравенства является множество
.
Эти точки разбивают числовую прямую на
три промежутка(-∞; x1),
(x1; x2),
(x2; +∞).Еслиa > 0, то
решением неравенства является множество![]() .
Еслиa < 0, то
решением неравенства является множество(x1;
x2).
.
Еслиa < 0, то
решением неравенства является множество(x1;
x2).
3) Если D = 0, то
график квадратного трехчлена касается
осиОхв точкех1,
являющейся единственным корнем уравнения![]() .
Приa < 0решением
неравенства будет пустое множество,
приa > 0– множество
.
Приa < 0решением
неравенства будет пустое множество,
приa > 0– множество![]() .
.
Пример 10. Решить неравенство
![]() .
.
Решение: Рассмотрим функцию
![]() .
Графиком этой функции является парабола,
ветви которой направлены вниз, так какa = -3 < 0.
.
Графиком этой функции является парабола,
ветви которой направлены вниз, так какa = -3 < 0.
Решим уравнение
![]() или
или![]() .
Корни этого уравнения
.
Корни этого уравнения![]() .
Изобразив схематически параболу
.
Изобразив схематически параболу![]() ,
найдем, чтоy < 0в каждом из промежутков (-∞; 1/3), (3; +∞).
,
найдем, чтоy < 0в каждом из промежутков (-∞; 1/3), (3; +∞).

Ответ:
![]() .
.
