
- •Тема №1. Арифметические вычисления. Проценты.
- •Обыкновенные дроби. Действия над обыкновенными дробями.
- •Дидактический материал.
- •Десятичные дроби. Действия над десятичными дробями.
- •Дидактический материал.
- •Процент. Основные задачи на проценты.
- •Дидактический материал.
- •Тема №2. Уравнения. Модуль числа.
- •Уравнения с одной переменной. Равносильность уравнений.
- •Решение уравнений с одним неизвестным, сводящихся к линейным.
- •Квадратные уравнения.
- •Квадратичная функция, ее график.
- •Уравнения, содержащие переменную под знаком модуля.
- •Дидактический материал.
- •Тема №3. Степени и корни.
- •3.1. Степень с целым показателем.
- •3.2. Арифметический корень. Степень с рациональным показателем.
- •3.3. Формулы сокращенного умножения.
- •4.2. Метод интервалов.
- •Дидактический материал.
- •Тема №5. Неравенства с одной переменной (часть II).
- •5.1. Неравенства, содержащие знак модуля.
- •5.2. Множество значений функции.
- •Дидактический материал.
- •Тема №6. Иррациональные уравнения.
- •Дидактический материал.
- •Тема №7. Показательные уравнения.
- •7.1. Методы решения показательных уравнений.
- •7.2. Классификация показательных уравнений.
- •Дидактический материал.
- •Тема №8. Показательные неравенства.
- •Дидактический материал.
- •Тема №9. Логарифмы.
- •Дидактический материал.
- •Тема №10. Преобразование тригонометрических выражений.
- •Дидактический материал.
- •Тема №11. Тригонометрические уравнения.
- •11.1. Решение простейших тригонометрических уравнений.
- •11.2. Основные методы решения тригонометрических уравнений.
- •11.3. Таблица значений тригонометрических функций.
- •Дидактический материал.
- •12.2.Стереометрия. Многогранники.
- •Дидактический материал.
- •12.3.Стереометрия. Круглые тела, тела вращения.
- •Дидактический материал.
Дидактический материал.
Найдите значение выражения:
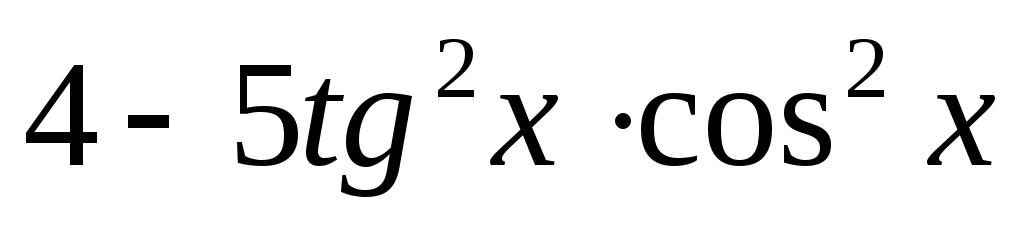 ,
если
,
если ;
; ,
если
,
если ;
; ,
если
,
если ;
; ,
если
,
если ;
; ,
если
,
если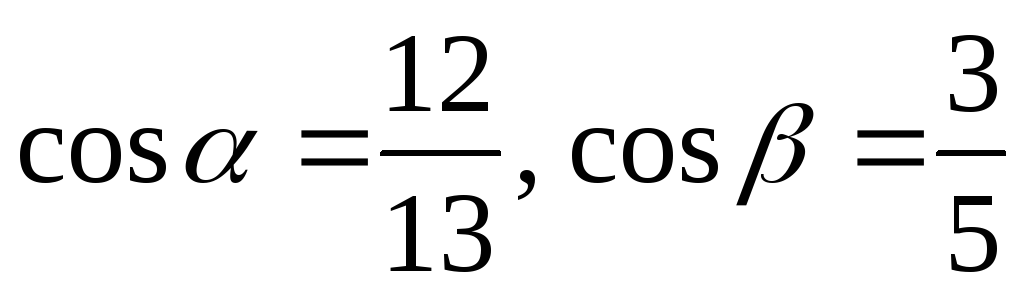 ,
а α и β – углыIчетверти;
,
а α и β – углыIчетверти;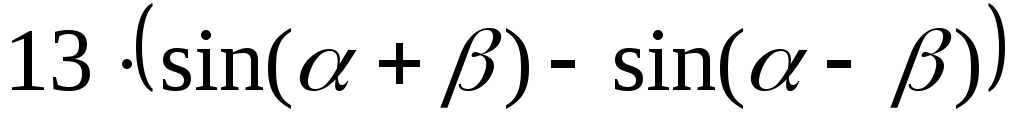 ,
если
,
если ;
а α и β – углыIчетверти;
;
а α и β – углыIчетверти; ,
если
,
если ;
;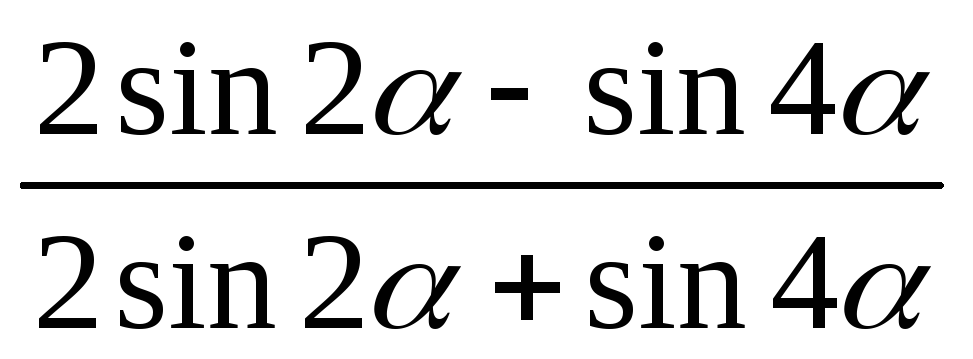 ,
если
,
если .
.
Вычислите:
 ,
если
,
если ;
;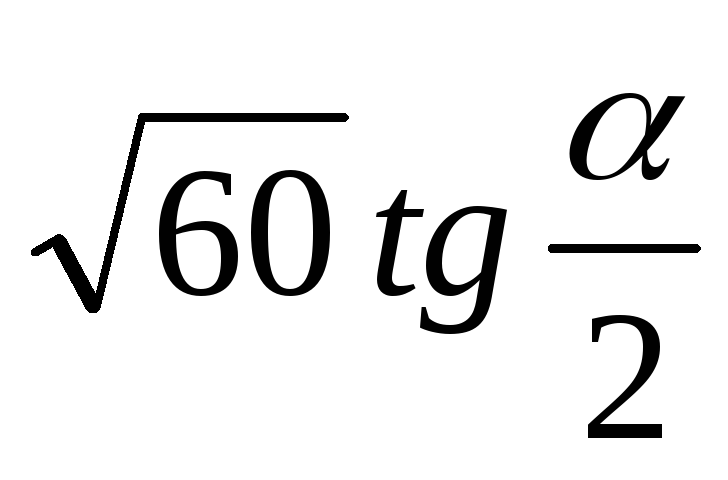 ,
если
,
если ;
; ,
если
,
если .
.
Упростите выражение:
 ; 13.
; 13. ;
;
 ; 15.
; 15. ;
;
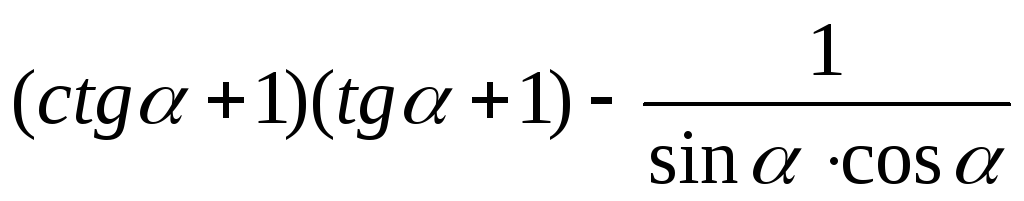 ;
; ; 18.
; 18. ;
;
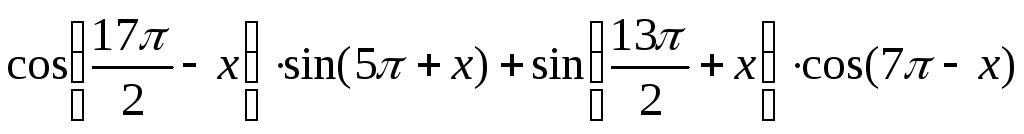 .
.
Преобразуйте в произведение:
 ;
; .
.
Найдите значение выражения:
 ; 23.
; 23. ;
;
 ; 25.
; 25. ; 26.
; 26. .
.
Ответы: 1. 0; 2. 5,92; 3. 10; 4. 3; 5. 5,2; 6. 6; 7. 3;
8. 3; 9. 1,24; 10. -10; 11. 7/25; 12. 1; 13. 2; 14. 0; 15. 0; 16. 2;
17. -1; 18. 2; 19. -1; 20.![]() ;
21.
;
21.![]() ;
22.
;
22.![]() ;
23.
;
23.![]() ;
24. 21; 25. 24; 26. 26.
;
24. 21; 25. 24; 26. 26.
Тема №11. Тригонометрические уравнения.
11.1. Решение простейших тригонометрических уравнений.
1º. Уравнение, содержащее неизвестную величину только под знаком тригонометрических функций, называется тригонометрическим. Тригонометрические уравнения либо не имеют корней, либо имеют их бесчисленное множество.
2º. Формула для корней уравнения
![]() ,
где
,
где![]() ,
имеет вид:
,
имеет вид:
![]() .
.
Уравнение
![]() при
при![]() решений не имеет.
решений не имеет.
Частные случаи:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() .
.
3º. Формула для корней уравнения
![]() ,
где
,
где![]() ,
имеет вид:
,
имеет вид:
![]() .
.
Уравнение
![]() при
при![]() решений не имеет.
решений не имеет.
Частные случаи:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() .
.
4º. Формула для корней уравнения
![]() при любом
при любом![]() имеет вид:
имеет вид:
![]() .
.
Частные случаи:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() .
.
5º. Формула для корней уравнения
![]() при любом
при любом![]() имеет вид:
имеет вид:
![]() .
.
Частные случаи:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() .
.
11.2. Основные методы решения тригонометрических уравнений.
1º. Уравнение вида
![]() (a0,
b0,
c0)равносильно уравнению
(a0,
b0,
c0)равносильно уравнению![]() ,
где
,
где![]() ,
,![]() .
.
Пример 40. Решить уравнение.
Решение:
![]()
![]() .
.
Ответ:
![]() .
.
2º. Одним из основных методов решения тригонометрических уравнений, так же как и других видов уравнений, является метод подстановки(замены переменной).
Пример 41. Решить уравнение
![]() .
.
Решение: Так как
![]() ,
то уравнение можно переписать следующим
образом:
,
то уравнение можно переписать следующим
образом:![]() ,
т.е.
,
т.е.![]() .
Полагая
.
Полагая![]() ,
приходим к квадратному уравнению
,
приходим к квадратному уравнению![]() ,
откуда
,
откуда![]() ,
и получаем совокупность двух простейших
уравнений
,
и получаем совокупность двух простейших
уравнений![]() .
Первое из них имеет решение
.
Первое из них имеет решение![]() ,
а второе решений не имеет.
,
а второе решений не имеет.
Ответ:
![]() .
.
Метод замены переменной полезен при решении так называемых однородных уравнений, т.е. уравнений вида
![]() (однородное
уравнениеIпорядка),
(однородное
уравнениеIпорядка),
![]() (однородное уравнениеIIпорядка).
(однородное уравнениеIIпорядка).
Если a0,
то при делении обеих частей первого
уравнения на![]() ,
а второго уравнения на
,
а второго уравнения на![]() получаем алгебраические уравнения,
решаемые подстановкой
получаем алгебраические уравнения,
решаемые подстановкой![]() .
Еслиa=0,
то во втором уравнении
.
Еслиa=0,
то во втором уравнении![]() выносится за скобки.
выносится за скобки.
Пример 42. Решить уравнение
![]() .
.
Решение: Разделив уравнение на
![]() ,
получим
,
получим![]() .
Пусть
.
Пусть![]() ,
тогда
,
тогда![]() или:
или:
1)
![]() ;
;
2)
![]() .
.
Ответ:
![]() .
.
Замечание 1.Уравнение вида![]() (d0)можно привести к однородному уравнениюIIпорядка, положив
(d0)можно привести к однородному уравнениюIIпорядка, положив![]() .
.
Замечание 2. Уравнение вида![]() (c0)можно привести к однородному уравнениюII порядка относительно
(c0)можно привести к однородному уравнениюII порядка относительно![]() и
и![]() .
.
3º. При решении тригонометрических уравнений также часто используют метод разложения на множители.
Пример 43. Решить уравнение
![]() .
.
Решение: Все члены уравнения переносятся в левую часть, после чего левую часть уравнения раскладывают на множители:
![]() .
.
Значит, либо
![]() ,
откуда
,
откуда![]() ,
либо
,
либо![]() ,
откуда
,
откуда![]() .
.
Ответ:
![]() .
.
Заметим, что для разложения на множители могут применяться различные формулы: формулы разложения тригонометрических функций в произведение, формулы понижения степени, формулы преобразования произведения в сумму и др.
Пример 44. Решить уравнение
![]() .
.
Решение: Согласно формуле (10.19) заменим произведение тригонометрических функций суммой, а затем воспользуемся формулой (10.15):
![]()
 .
.
Ответ:
![]() .
.
Пример 45. Решить уравнение
![]() .
.
Решение: Это уравнение можно привести
к квадратному относительно
![]() ,
понизив степень
,
понизив степень![]() и
и![]() ,
но существует более короткий способ.
,
но существует более короткий способ.
Дополним левую часть уравнения до
полного квадрата суммы, для чего прибавим
![]() к обеим частям уравнения. Получим
уравнение равносильное данному:
к обеим частям уравнения. Получим
уравнение равносильное данному:
![]() ;
;
![]() .
.
Применяя формулы (10.1) и (10.10), получаем:
![]() .
.
Пусть
![]() .
Тогда
.
Тогда![]() ;
;![]() (не удовлетворяет условию
(не удовлетворяет условию![]() ),
),![]() .
Так как
.
Так как![]() ,
то
,
то![]() ,
,
![]() .
.
Ответ:
![]() .
.
