Дидактический материал.

Вычислите:

1. ; 2.; 3.; 4.;

5. ; 6.; 7.;

8. ; 9.; 10.;

11. ; 12..

13. Прологарифмируйте по основанию 3 выражение .

14. Прологарифмируйте по основанию 5 выражение .

15. Прологарифмируйте по основанию 4 выражение .

16. Вычислите x, если.

17. Вычислите x, если.

Вычислите значение выражения:

18. при;

19. при;

20. при;

21. при.

Упростите выражение:

22. ; 23.;

24. ; 25..

26. Известно, что . Найдите.

27. Найдите значение выражения , если.

28. Найдите значение выражения , если.

29. Найдите значение выражения , если.

30. Найдите значение выражения , если.

Найдите значение функции:

31. при;

32. при.

Тема №10. Преобразование тригонометрических выражений.

1º. На плоскости xOyрассмотрим окружность с центром в начале координат и радиусом, равным 1. На единичной окружности отметим точкуA(1;0). РадиусOAназывают начальным радиусом. При повороте начального радиуса на угол α около центра О точка А(1;0) перейдет в некоторую точку М(x;y). Заметим, что поворот можно осуществить по часовой стрелки (угол поворота положителен) или против часовой стрелки (угол поворота отрицателен).

Косинусомугла α называется абсцисса точки М:.

Синусомугла α называется ордината точки М:.

Тангенсомугла α называется отношение ординаты точки М к ее абсциссе:.

Котангенсомугла α называется отношение абсциссы точки М к ее ординате:.

являются тригонометрическими функциями аргумента α.

2º. Единицами измерения величины угла являются градусирадиан.

Если начальный радиус окружности совершит один полный оборот, то получится угол, равный 360˚ или 2π радиан.

Связь между градусной и радианной мерами измерения угла: рад.

Из этой формулы следует:

а) ; б); в); г); д)и т.д.

3º. Свойства тригонометрических функций:

Функции - нечетные функции:

.

Функция - четная:.

Функции - периодические с наименьшим периодом 2π:

.

Функции - периодические с наименьшим периодом π:

.

4º. Основное тригонометрическое тождество.

Согласно теореме Пифагора (“в прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы”) координаты любой точки М(x;y) единичной окружности удовлетворяют уравнению:. Отсюда:

где(10.1)

Из этой формулы следует:

а) ; б).

5º. Основные соотношения между тригонометрическими функциями:

, (10.2)

, (10.3)

, (10.4)

, (10.5)

. (10.6)

6º. Формулы сложения аргументов:

, (10.7)

, (10.8)

. (10.9)

7º. Формулы двойного аргумента:

, (10.10)

, (10.11)

. (10.12)

8º. Формулы понижения степени синуса и косинуса:

. (10.13)(10.14)

9º. Преобразование суммы и разности одноименных тригонометрических функций в произведение:

, (10.15)

, (10.16)

, (10.17)

. (10.18)

10º. Преобразование произведения тригонометрических функций в сумму:

, (10.19)

, (10.20)

. (10.21)

11º. Выражение тригонометрических функций через тангенс половинного аргумента.

При доказательстве тождеств, решении тригонометрических уравнений и т.п. часто возникает необходимость выразить все 4 тригонометрические функции через какую-нибудь одну функцию f(x). Для этого пользуются следующими формулами:

а) , (10.22)

б) , (10.23)

в) . (10.24)

12º. Формулы приведения. Это соотношения, при помощи которых значения тригонометрических функций аргументоввыражают через тригонометрические функции угла α. Все формулы приведения можно свести в следующую таблицу:

Аргумент t Функция
sin t	cos α	cos α	sin α	- sin α	-cos α	-cos α	-sin α	sin α
cos t	sin α	-sin α	-cos α	-cos α	-sin α	sin α	cos α	cos α
tg t	ctg α	-ctg α	-tg α	tg α	ctg α	-ctg α	-tg α	tg α
ctg t	tg α	-tg α	-ctg α	ctg α	tg α	-tg α	-ctg α	ctg α

Пример 34. Найдите , если.

Решение: . По формуле (10.6). Так как α находится в 3-ей четверти, тои, следовательно,. Ответ:.

Пример 35. Вычислить значение выражения , если.

Решение: Используем формулу (10.10), а затем числитель и знаменатель дроби разделим на . Тогда:

Ответ: 9,25.

Пример 36. Доказать тождество: .

Решение: Используя формулы (10.15), (10.16), получим:

.

Пример 37. Вычислить , если.

Решение: Выразив ичерезпо формулам (10.22), (10.23), получим:

.

Ответ: ¼.

Пример 38. Упростить выражение: .

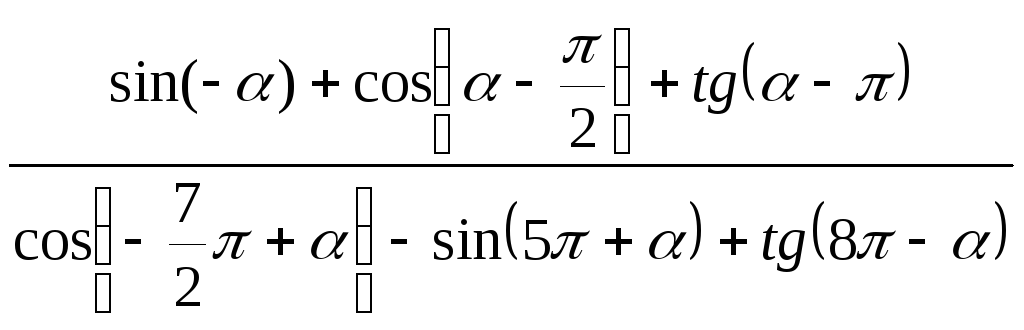Решение: Воспользуемся свойствами четности и нечетности тригонометрических функций, а также выделим период в аргументе функций и исключим его, опираясь на свойство периодичности функций:

,

,

,

,

.

Получаем:

Далее используем формулы приведения:

.

Ответ: -1.

Пример 39. Найти .

Решение: Воспользуемся формулой приведения и определением котангенса:

.

Поскольку угол находится в 4-ой четверти, то. Получаем:

.