
- •Лекція 7: Основні поняття теорії ймовірностей.
- •1. Предмет теорії ймовірностей. Випробування, події, класифікація подій.
- •2.1. Класичне і статистичне означення ймовірності
- •2.2. Статистичне означення ймовірності.
- •Сума і добуток двох подій, їх властивості
- •4. Повторні незалежні випробування. Схема Бернуллі.
- •4.2. Формула Бернуллі.
- •4.4. Інтегральна формула Муавра-Лапласа
- •4.5. Ймовірність відхилення відносної частоти успіху.
- •4.6. Формула Пуассона
- •4.7. Простий потік подій
4. Повторні незалежні випробування. Схема Бернуллі.
Схема Бернуллі або схема повторних незалежних випробувань:
Розглянемо випадки, коли у дослідах одні і ті ж випробування повторюються декілька разів. (Наприклад: підкидання монети; схожість насіння; наявність бракованих виробів у партії і т.д.). Тоді в результаті кожного випробування може з’явитись або не з’явитись подія, яка нас цікавить. (Наприклад: поява герба або решки; проросло зерно чи не проросло; деталь бракована чи стандартна і т.д.). Але цікавим для нас є не результат окремого випробування у серії проведених дослідів, а ймовірність появи тієї чи іншої кількості подій у серії випробувань.
У
схемі Якоба Бернуллі (1654-1705р.) розглядається
серія з n
повторних незалежних випробувань, кожне
з яких має лише два наслідки: поява
деякої події А
(успіх)
або поява протилежної події
 (невдача),
причому ймовiрність успіху однакова в
усіх випробуваннях і дорівнює р.
Числа n
і р
називаються параметрами
схеми Бернуллі. Тоді узагальнимо вище
сказане у вигляді схеми:
(невдача),
причому ймовiрність успіху однакова в
усіх випробуваннях і дорівнює р.
Числа n
і р
називаються параметрами
схеми Бернуллі. Тоді узагальнимо вище
сказане у вигляді схеми:
1. Проводится n незалежних випробувань.
2. Ймовірність
успіху стала і дорівнює p,
де
 .
.
3. Ймовірність
невдачі
 .
.
4. Кожне випробування має два наслідки: успіх або невдача.
4.2. Формула Бернуллі.
Схожість
зерна дорівнює
 .
Знайти ймовірність, що зn
посіяних зернин проросте k
насінин.
.
Знайти ймовірність, що зn
посіяних зернин проросте k
насінин.
Подія А-успіх полягає у тому, що зернина проросте.
Ймовірність
того, що в n
незалежних
випробуваннях, у кожному з яких ймовірність
появи події дорівнює p
( ),
подія настане рівноk
разів
(без різниці, в якій послідовності),
обчислюється за формулою Бернуллі:
),
подія настане рівноk
разів
(без різниці, в якій послідовності),
обчислюється за формулою Бернуллі:  ,
де
,
де .
.
(Для
прикладу з насінням, задача формулюється
наступним чином: ймовірність того, що
з
 насінин проросте рівно
насінин проросте рівно ,
якщо ймовірність проростання для кожної
насінини дорівнює
,
якщо ймовірність проростання для кожної
насінини дорівнює ,
обчислюємо за формулою Бернуллі).
,
обчислюємо за формулою Бернуллі).
Примітка:
формула Бернуллі застосовується у
випадку, коли кількість випробувань
відносно невелика (як правило, при
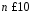 ,
дер
не може бути набагато меншим 0,1, оскільки
при піднесенні до степеня, результат
прямуватиме до 0).
,
дер
не може бути набагато меншим 0,1, оскільки
при піднесенні до степеня, результат
прямуватиме до 0).
Приклад №1. У корзині 30 білих і 10 чорних куль. Взяли підряд п’ять куль, причому кожну взяту кулю повертають у корзину назад перед тим, як брати наступну. Яка ймовірність того, що з п’яти взятих куль три будуть білими?
Розв’язання.
Ймовірність
взяти білу кулю можна вважати однаковою
(сталою в усіх п’яти випробуваннях і
рівною:
 ),
тоді ймовірність витягти чорну (не
білу):
),
тоді ймовірність витягти чорну (не
білу): ,
або
,
або .
Скориставшись формулою Бернуллі,
матимемо:
.
Скориставшись формулою Бернуллі,
матимемо:

Відповідь: 26,4%.
Частіше на практиці цікавить ймовірність того, що у випробуваннях подія А з’явиться: а) менше k разів; б) більше k разів; в) не менше k разів; г) не більше k разів, тоді її визначають відповідно за формулою:
 ,
або:
,
або:

Приклад №2. Ймовірність того, що витрати води протягом дня не перевищуватимуть норму, дорівнює 0,8. Знайти ймовірність того, що витрати води будуть у нормі у найближчі шість днів протягом: 1) п’яти; 2) не менше чотирьох.
Розв’язання.
Будемо
вважати, що випробування – це перевірка
норм витрат води. Кількість випробувань
за умовою n
= 6. Подія
А
– успіх витрати води в нормі, тоді
 ,
не відповідають нормам витрати води
,
не відповідають нормам витрати води
 .
.
За формулою Бернуллі маємо:

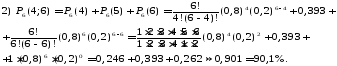
Відповідь: 1) 39,3%; 2) 90,1%.
Локальна теорема Муавра-Лапласа
Для
частинного випадку, а саме для
 асимптотична формула була знайдена у
1730 р. Муавром, у 1783 р. Лаплас узагальнив
формулу Муавра для будь-якого
асимптотична формула була знайдена у
1730 р. Муавром, у 1783 р. Лаплас узагальнив
формулу Муавра для будь-якого ,
відмінного від 0 і 1.
,
відмінного від 0 і 1.
Локальна теорема Лапласа. Ймовірність того, що в n незалежних випробуваннях, у кожному з яких ймовірність появи події дорівнює p (0<p<1), подія настане рівно k разів (без різниці, в якій послідовності ), наближено дорівнює:
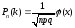 ,
де
,
де та
та 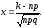 ,причому
,причому
 .
.
Властивості
функції
 :
:
 –парна;
2. якщо
–парна;
2. якщо
 ,
то
,
то .
.
Таблиця
значень функції
 для додатніх значеньх
міститься
в додатку 1 [1, с.461-462; 2, с.197].
для додатніх значеньх
міститься
в додатку 1 [1, с.461-462; 2, с.197].
Приклад №3. Серед виготовлених деталей в середньому 0,5% браку. Яка ймовірність, що в партії з 10000 деталей 40 бракованих?
Розв’язання.
Випробування
– перевірка якості деталей при кількості
випробувань n=10000.
Подія А – успіх – деталь бракована,
тоді р=0,005, q=0,995,
k=40,
 Застосуємо
локальну формулу Лапласа:
Застосуємо
локальну формулу Лапласа:
 .
.
Відповідь: ймовірність того, що в партії із 10000 деталей 40 бракованих – 2,06%.
