2.8 Подбор арматуры поперечного ребра

Подбор арматуры поперечного ребра выполняем как для изгибаемого элемента таврового профиля с полкой в сжатой зоне высотой h, фактической ширинойb_f, защитный слой принимаем а = 25мм.

Рис. 2.12. Фактическое сечение поперечного ребра

Исходные данные:

h= 200мм

b_f= 1150мм

а = 25мм

В25 (R_b= 14.5 МПа)

А400 (R_S= 355 МПа)

γ_n = 0.95

М = 0.583 кН∙м

Решение:

Принимаем значение вводимое в расчёт b`_f= 400мм

h₀=h–a= 200 – 25 = 175мм

Расчет производим, предполагая что сжатая арматура не требуется

условие выполняется, следовательно нейтральная ось проходит в полке.

Дальнейший расчет ведем как для прямоугольного сечения шириной b`_f= 400мм

Значение

из полученного условия следует, что сжатая арматура не требуется.

Определяем площадь растянутой арматуры:

Подбираем растянутую арматуру 1Ø6 класса А400, в этом случае

В верхней зоне для создания плоского каркаса конструктивно устанавливаем стержень Ø6 арматуры класса А240

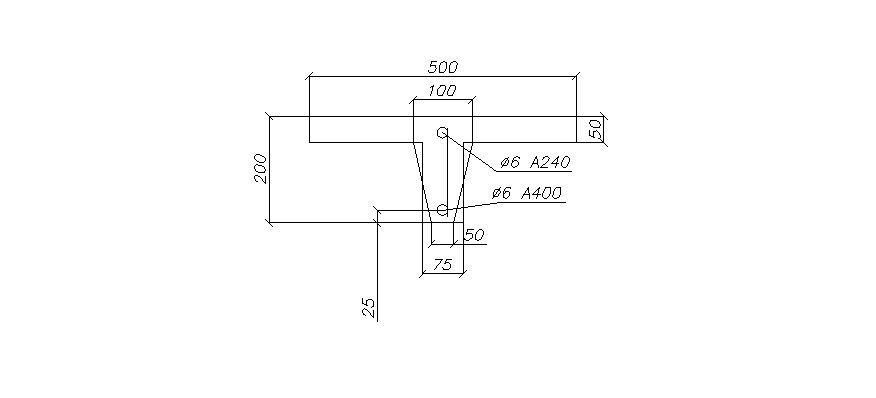
Рис. 2.13 Армирование поперечного ребра

2.9 Подбор арматуры продольного ребра

Подбор арматуры продольного ребра выполняем как для изгибающего элемента таврового сечения высотой h=400мм и фактической ширинойb_f=1180мм.

Рис.2.13 Фактическое сечение продольного ребра

Исходные данные:

h= 400мм

b_f= 1180мм

а = 35мм

В25 (R_b= 14.5 МПа)

А540 (R_S= 450МПа)

γ_n = 0.95

М = 32.72 кН∙м

Решение:

Принимаем значение, вводимое в расчет 1185мм. Арматура класса А540 (R_s=450 МПа)R_sп=540 МПа . Зададимся величиной предварительного напряжения

С учетом потерь

Расчет по прочности нормальных сечений производим в зависимости от соотношений ξ:

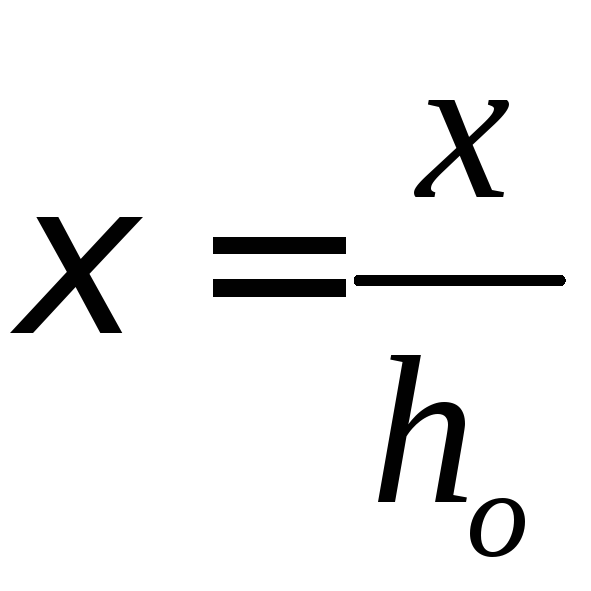и

где ơ_spпринимается с учетом всех потерь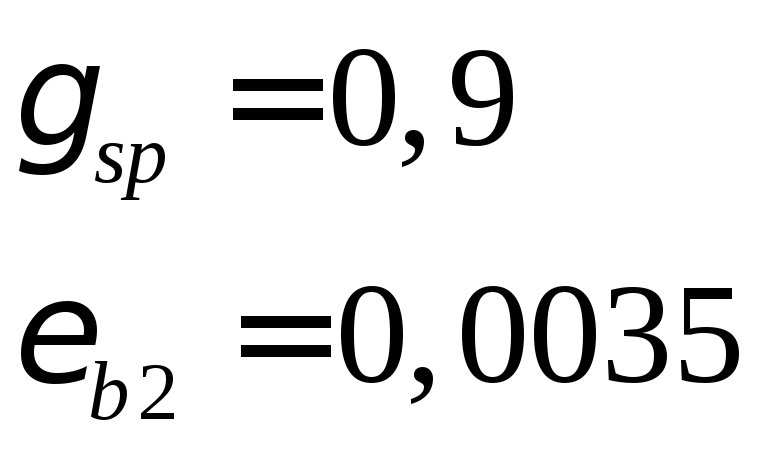

Определяем положение нейтральной оси, в предположении, что сжатой арматуры не требуется:

условие выполняется, следовательно нейтральная ось находится в полке.

Расчет ведем по прямоугольному сечению.

Вычисляем α_тпо формуле:

сжатой арматуры не требуется.

значит

коэффициент условия работы

2 Ø 12 А540 (А_sp=226 мм2)

В верхней и нижней зонах в продольных ребрах для обеспечения плоского каркаса конструктивно устанавливаем 2 стержня Ø 10 арматуры А240

Рис.2.14 Армирование продольного ребра

3. Расчет элементов плиты по наклонным сечениям

3.1 Расчет поперечного ребра

3.1.1 Расчет по наклонным сечениям от действия поперечной силы

Расчет изгибаемых элементов по наклонному сечению производим по следующим условиям:

Где Q– поперечная сила в наклонном сечении с длинной проекции С от внешних сил, расположенных по одну сторону от рассматриваемого наклонного сечения,

Q_{В –} поперечная сила, воспринимаемая бетоном в наклонном сечении,

Q_{В –} поперечная сила, воспринимаемая хомутами в наклонном сечении.

где

При расчете элемента на действие равномерно распределенной нагрузки q₁, не выгоднейшее значение принимают равным:

Так как нагрузка qвключает в себя временную нагрузку, которая приводится к эквивалентной по методу равномерно распределенной нагрузки, тоq₁

При этом

где Q_мах– поперечная сила в опорном сечении

Рис. 2.16 Расчетная схема поперечного ребра.

Определим эквивалентную нагрузку, действующую на поперечное ребро.

Для этого определим расчетные нагрузки, действующие на наклонное сечение

Определим нужно ли устанавливать поперечную арматуру по расчету. Для этого необходимо проверить выполнение следующих условий

Условия выполняются, т.е. поперечной арматуры по расчёту не требуется.

Так как высота балки больше 150 мм, то поперечную арматуру следует устанавливать конструктивно.

Зададимся шагом поперечной арматуры

Принимаем шаг поперечной арматуры S=100 мм.

Из условия свариваемости при Ø продольной арматуры 10 А400

Определим наименьший допустимый диаметр поперечной арматуры 3 мм.

Принимаем арматуру Ø3 В500

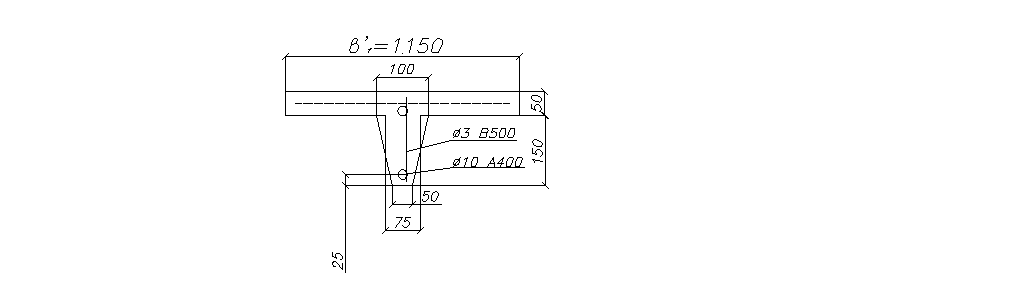
Рис. 2.17 Армирование поперечного ребра

Рис. 2.18 Каркас поперечного ребра

Спецификация арматуры поперечного ребра

Таб.

КР-1	Кол-во, шт.	Масса един., кг	Общая масса, кг
10 А400 ГОСТ6727-80*1=1030	1	1.03*0.617=0.635	0.635
3 В500 ГОСТ6727-80*1=150	11	0.15*0.055=0.0083	0.0913
10 А240 ГОСТ6727-80*1=1030	1	1.03*0.617=0.635	0.635