Лабораторная работа №8

Линейное программирование

Решение транспортной задачи

Постановка задачи:

Имеется m поставщиков, которые обозначены , у которых сосредоточен однородный груз в количестве .

Груз требуется перевезти n потребителям обозначенных в количестве . Также известна стоимость перевозок от i-го поставщика j-тому потребителю, выраженной матрицей 

,

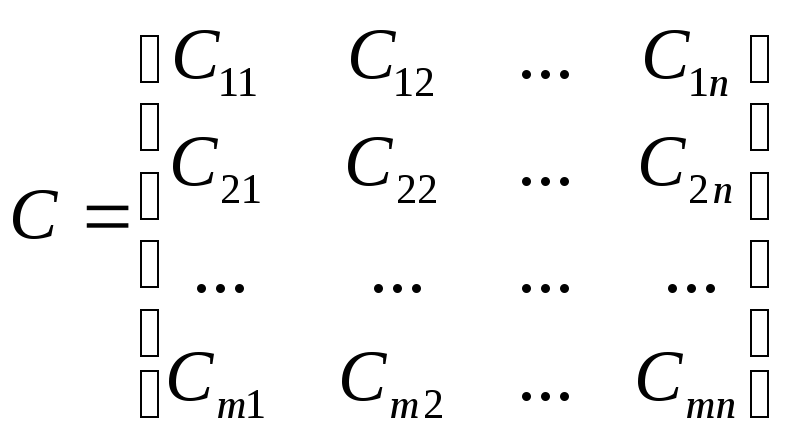где − стоимость перевозки 1 единицы груза от i-того поставщика j‑тому потребителю.

Требуется составить такой план перевозки груза, при котором, общая стоимость перевозки будет минимальной. Для удобства решения сведем данные задачи в следующую таблицу:

Потребитель Поставщик			…		Запасы
			…
			…
…	…	…	…	…	…
			…
Потребности			…

Введем неизвестное в задаче − количество груза, которое необходимо перевезти от i-того поставщика к j-тому потребителю.

Таким образом, можно сформулировать математическую постановку задачи:

Требуется найти минимум функции цели (целевая функция):

Функция F представляет собой общую стоимость всего перевозимого груза при следующих ограничениях:

1. ограничения на потребности

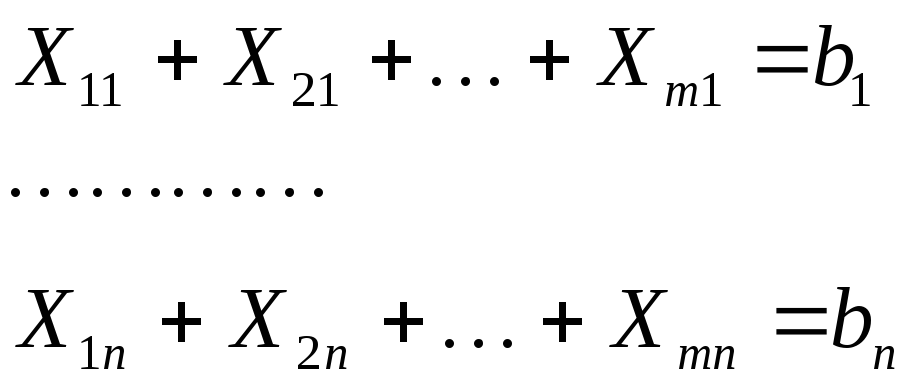
2. ограничения на запасы

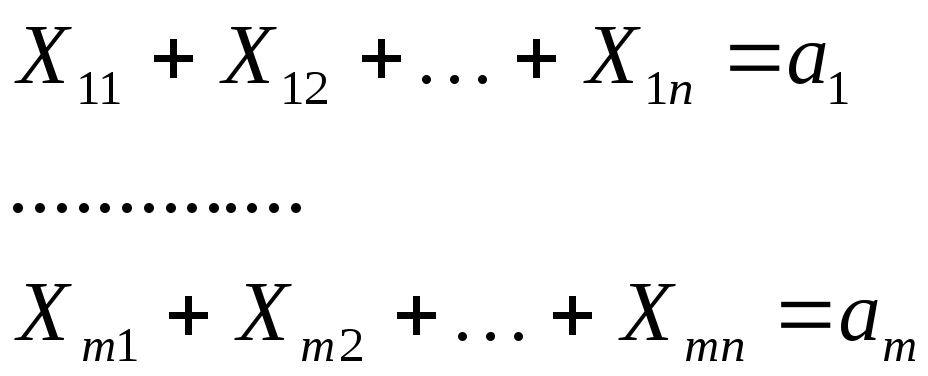
3) количество груза не может быть отрицательным, также может быть наложено условие, чтобы Х представлялось целым числом.

, целое.

Теорема.

Транспортная задача разрешима только и только тогда, когда . Сумма всех запасов равна сумме всех потребностей.

Транспортная задача, для которой выполняется данное условие, называется закрытой транспортной задачей. Если выполняется условие , то такая транспортная задача называется открытой. Для перевода открытой задачи в закрытую задачу вводится фиктивный поставщик , запасы которого определяются по формуле: . Если выполняется условие , то такая задача также является открытой. Для перевода ее в закрытую задачу вводится фиктивный потребитель с потребностями . Соответственно стоимость перевозок полагается равными 0.

Пример 1.

Для строительства 4-х объектов используется кирпич, изготавливаемый на 3-х заводах. Ежедневно каждый из заводов может производить 100, 150 и 50 усл. ед. кирпича. Ежедневная потребность в кирпиче на каждом строительном объекте равна соответственно 70, 80,60 и 90 усл.ед. Поскольку произведенный кирпич (100 + 150 + 50 = 300 усл.ед.) весь потребляется объектами (70 + 80 + 60 + 90 = 300 усл. ед.) ,то задача является закрытой. Известны также тарифы (руб.) перевозок 1-й усл. ед. кирпича с каждого из заводов каждому из строящихся объектов .

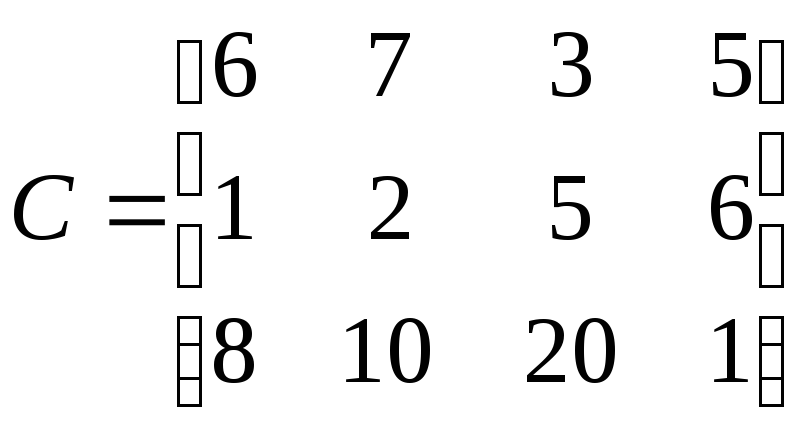Составим план, при котором общая стоимость перевозок будет минимальной.

Решение примера:

Для удобства решения сведем данные примера в следующую таблицу:

	Стоимость перевозки 1 усл. ед. кирпича, руб.				Возможности
	Объект 1	Объект 2	Объект 3	Объект 4
Завод 1	6	7	3	5	100
Завод 2	1	2	5	6	150
Завод 3	8	10	20	1	50
Потребности	70	80	60	90

Составление математической модели.

1) Вводим неизвестные. Так как необходимо составить план перевозок кирпича, то обозначим через количество условных единиц кирпича которое необходимо перевести с i-того завода j-тому строящемуся объекту. Таким образом, получаем 12 неизвестных.

2) Целевая функция. Так как необходимо составить план перевозок минимизирующий стоимость, то целевая функция примет вид:

F = 6 + 7 + 3 + 5 + 1 + 2 + 5 + 6 + 8 + 10 + 20 + 1

3) Ограничения.

Ограничения на потребности:

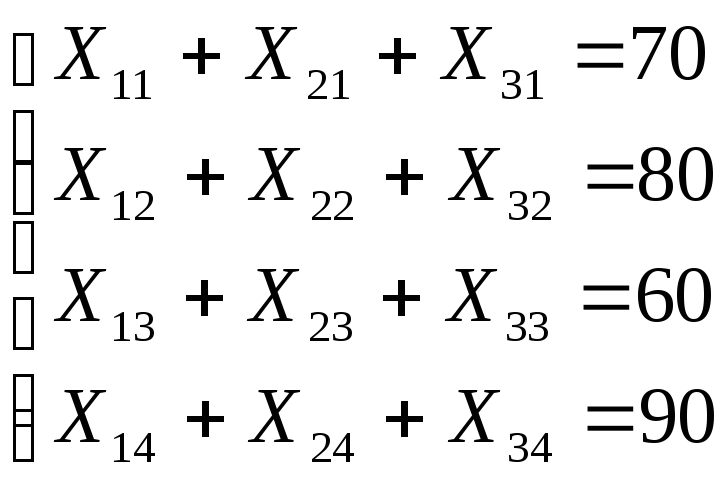
Ограничения на возможности:

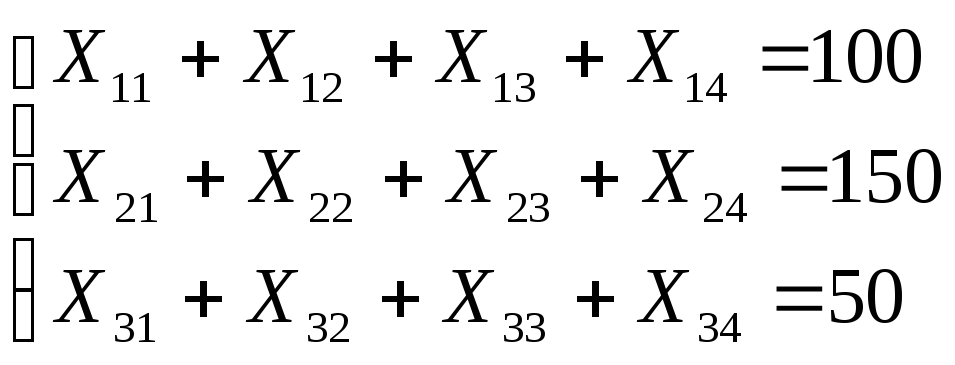
− целые числа

Решение примера средствами MS Excel

На начальном этапе неизвестным присваиваются произвольные значения. В нашем примере мы положим, что =1.

В MS Excel заносится функция, соответствующая только левым частям ограничений.

На рабочем листе книги MS Excel создается экранная форма (рис. 1), в которую заносятся формулы:

В ячейку F14 =СУММ(В14:E14).

В ячейку F15 =СУММ(В15:E15).

В ячейку F16 =СУММ(В16:E16).

В ячейку B17 =СУММ(В14:B16).

В ячейку C17 =СУММ(C14:C16).

В ячейку D17 =СУММ(D14:D16).

В ячейку E17 =СУММ(E14:E16).

В ячейку B20 =СУММПРОИЗВ(B7:E9; B14:E16).

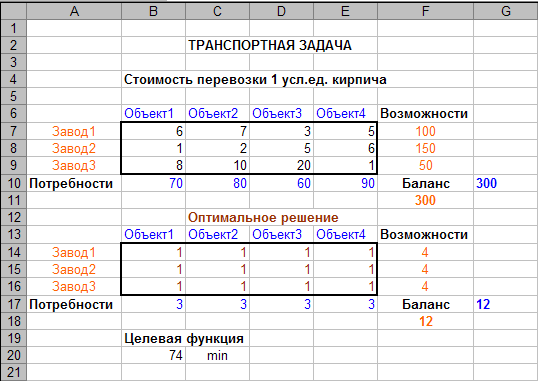
Рис. 1.

Используем инструмент Поиск решения. Установим курсор в ячейку с целевой функцией (В20) и выполним команду лента Данные  Поиск решения. В открывшемся диалоговом окне (рис. 2) заполним позиции: Установить целевую ячейку: $B$20; Равной: минимальному значению; Изменяя ячейки: $B$14:$E$16; Ограничения: $B$17 = 70, $C$17 = 80, $D$17 = 60, $E$17 = 90, $F$14 = 100, $F$15 = 150; $F$16 = 50, $B$14:$E$16 >= 0, $B$14:$E$16 = целое. Затем произведем вычисления нажав кнопку Выполнить после чего откроется окно Результаты поиска решения (рис. 3).

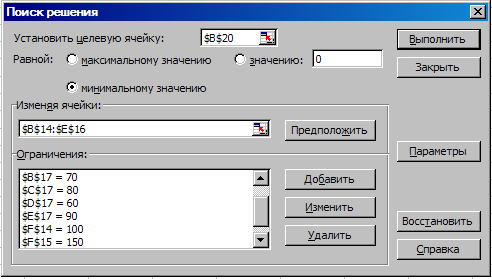
Рис.2.

Рис. 3.

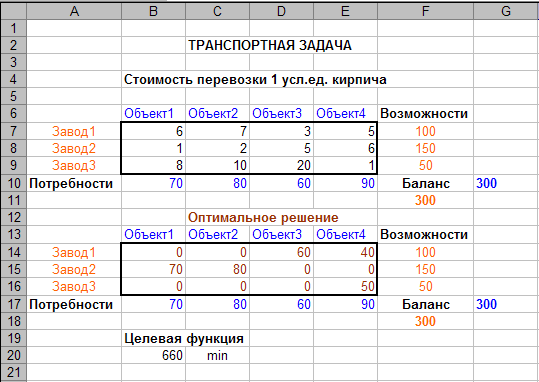
Рис. 4.

В результате решения примера переменные в ячейках B14:E16 примут следующие значения:

.

Как видно из рисунка 4 при выполнении всех ограничений, баланс между кирпичом произведенным заводами и кирпичом, потребленным строительными объектами сохранился (300 усл.ед.).

Минимальная стоимость перевозки кирпича (значение целевой функции в ячейке В20) составила F = 660 усл.ед. Которая будет достигнута при обеспечении кирпичом: Заводом1 Объекта3 (60 усл.ед.) и Объекта2 (40 усл.ед.); Заводом2 Объект1 (70 усл.ед.) и Объект2 (80 усл.ед.); Завод3 обеспечивает кирпичом Объект4 (50 усл.ед.).

Представим результаты решения диаграммой (рис. 5).

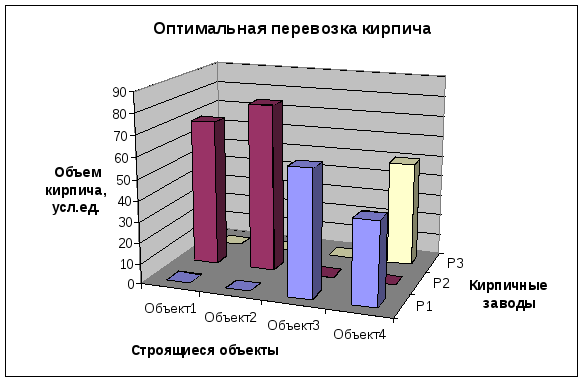
Рис. 5.

Р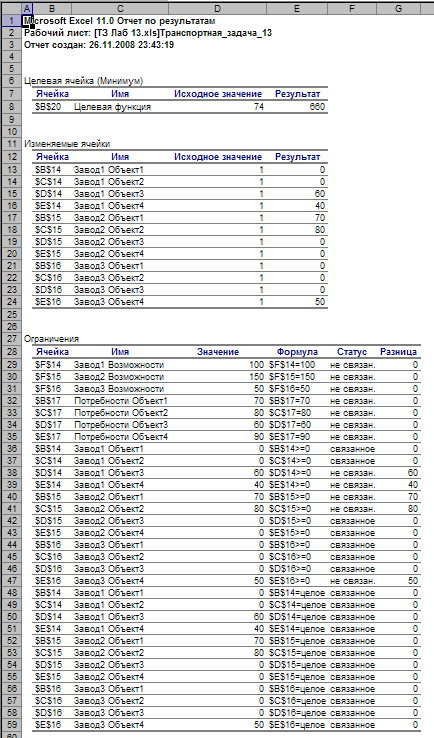 езультаты решения примера представлены в окне Тип отчета: Результаты (рис. 6) на основании которого проведем анализ полученного решения.

Рис. 6.

Отчет состоит из трех таблиц. Таблица 1 приводит сведения о целевой функции. В столбце Исходное значение приведено значение целевой функции до начала вычислений − 74, а в столбце Результат − значение целевой функции в оптимальном решении − 660. Таблица 2 приводит значения искомых переменных, полученные в результате решения задачи. Таблица 3 показывает результаты оптимального решения для ограничений задачи: возможности заводов по производству кирпича и потребление кирпича стоящимися объектами. В столбце Формула приведены ограничения в том виде, в котором они были введены в диалоговом окне Поиск решения, в столбце Значение приведены величины используемого ресурса. В графе Разница показано количество неиспользованного ресурса. Если ресурс используется полностью, то в столбце Состояние указывается связанное; при неполном использовании ресурса в этом столбце указывается не связанное.