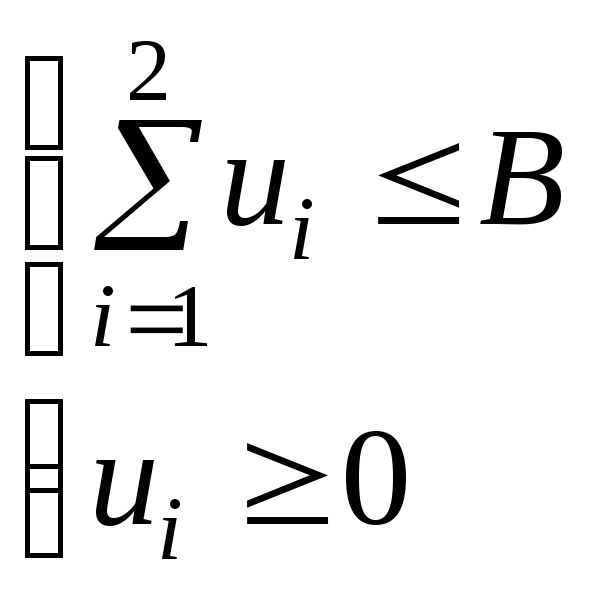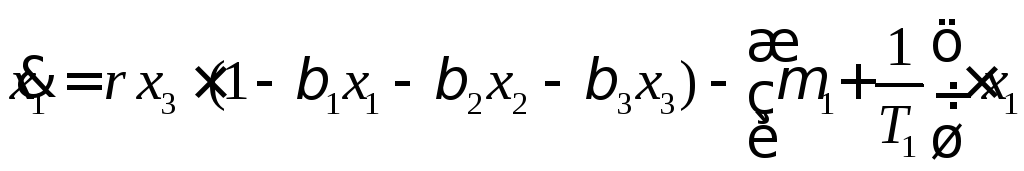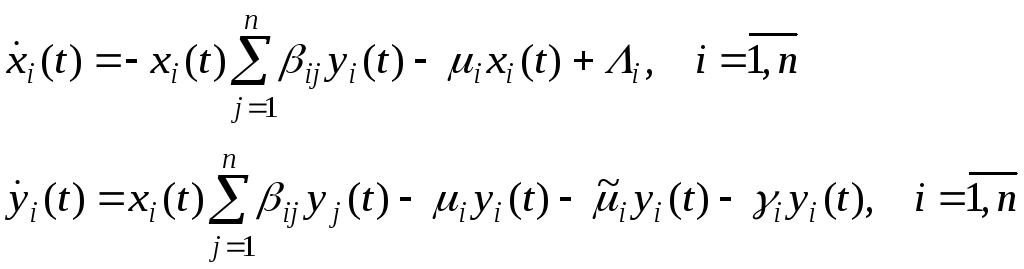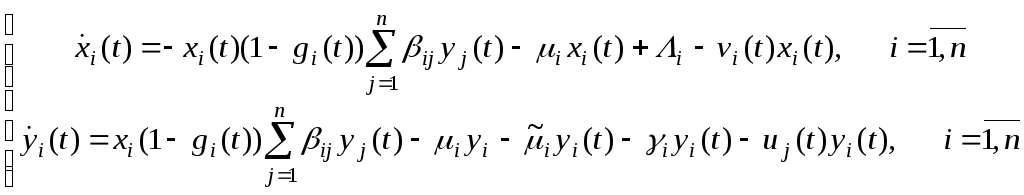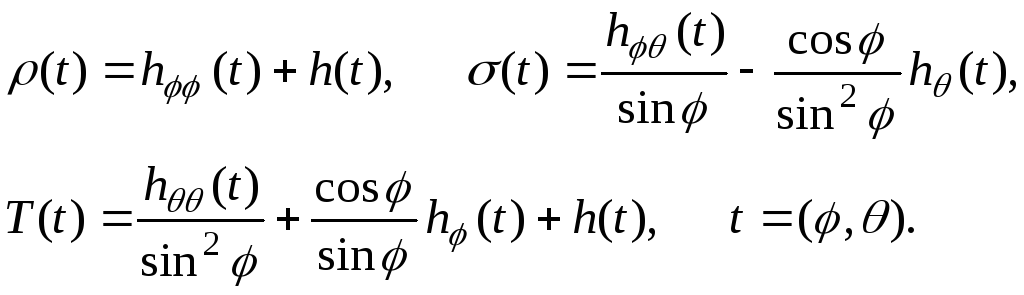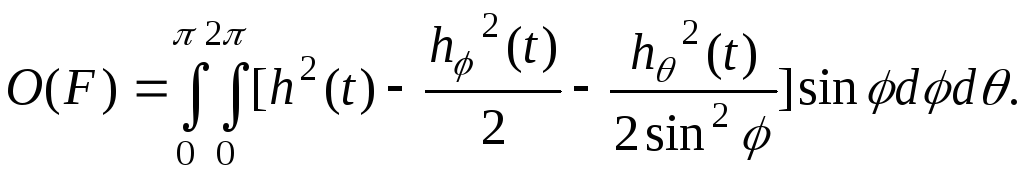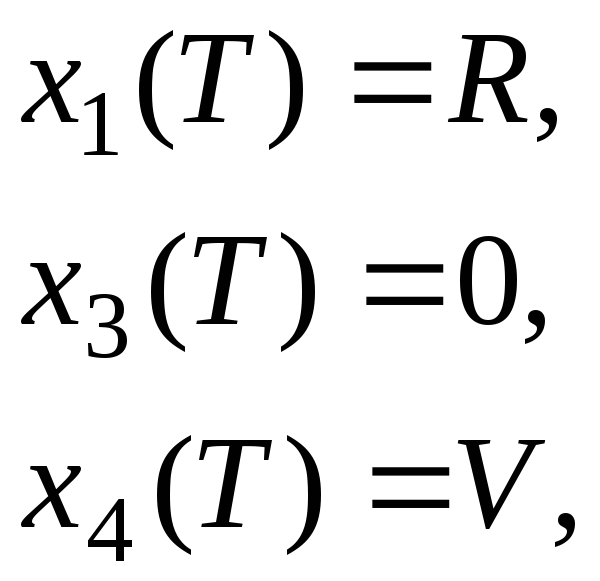Тема 12. Нейронная сеть, описываемая системой интегро-дифференциальными уравнениями. Учет эффекта запаздывания сигнала в нейронных сетях. Случай малого запаздывания.

Типовое задание.

№ 1. Для следующих моделей нейронной сети применить необходимые условия оптимальности и исследовать зависимость решения от величины запаздывания. Динамические свойства систем связанных "нейронов" могут быть смоделированы следующими системами нелинейных дифференциальных уравнений

а)

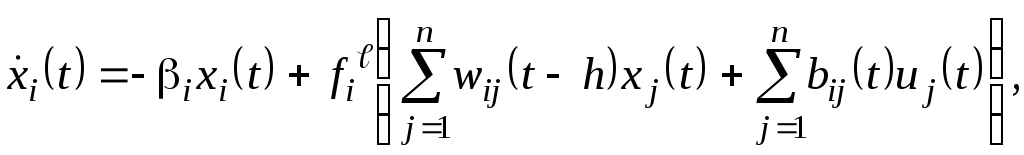
б)

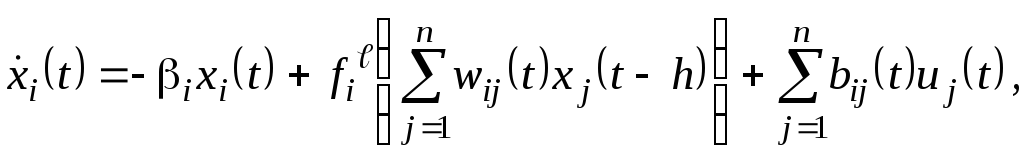
в)

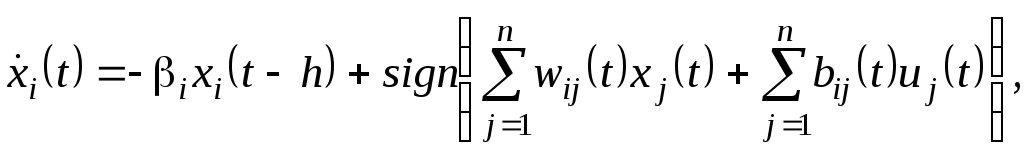
Здесь каждая функция , , есть действительная функция состояния -го "нейрона", функция , , является внешним воздействием на -й "нейрон". Коэффициенты , , обозначают веса или "синоптические связи", - интенсивность внешних воздействий. Функции (функции активации) характеризуют, как -й "нейрон" реагирует на совокупный сигнал. Некоторые авторы полагают, что изменяя внешний сигнал можно управлять каждым нейроном, но разумно предположить, что число таких входов гораздо меньше, чем число функций состояния, т.е. .

Весовые коэффициенты и внешние сигналы должны быть выбраны так, чтобы минимизировать заданный функционал

с учетом следующих ограничений на весовые коэффициенты и внешние воздействия:

,

где - заданные положительные числа.

Приложение 2. Темы курсовых работ

Примерные темы курсовых проектов

1. Оптимальное управление в области рекламной деятельности с целью увеличения объема продаж.

Требуется выработать оптимальную политику в области рекламной деятельности, которая стимулирует объем продаж данного продукта за некоторый период времени при следующих условиях: скорость изменения объема продаж уменьшается пропорционально объему продаж и увеличивается пропорционально уровню рекламной деятельности в этой части рынка, которая этим продуктом не насыщена. Задача имеет вид

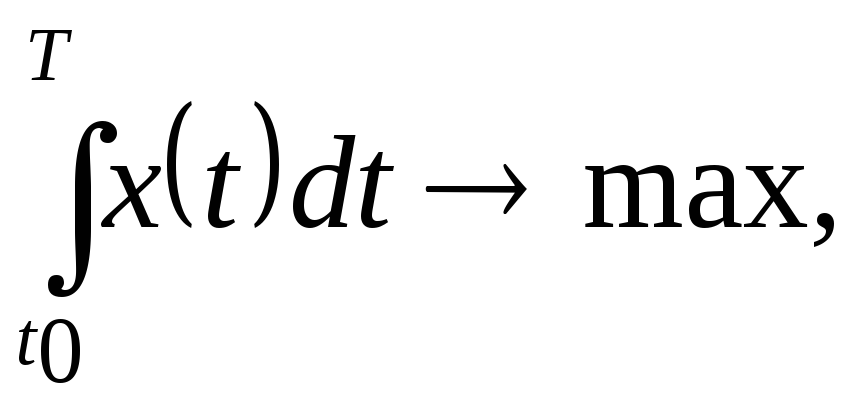
где − объем продаж в единицу времени;− уровень рекламной деятельности; М – емкость рынка;− заданные положительные параметры;− начальный и конечный моменты времени соответственно;− показатель скорости продаж,− эффективности рекламной деятельности;− начальный объем продаж; А − максимальный уровень рекламной деятельности.

2. Оптимальное управление в области рекламной деятельности с учетом дисконтирования прибыли.

Требуется выработать оптимальную политику в области рекламной деятельности, которая стимулирует объем продаж данного продукта за некоторый период времени при следующих условиях: скорость изменения объема продаж уменьшается пропорционально объему продаж и увеличивается пропорционально уровню рекламной деятельности в этой части рынка, которая этим продуктом не насыщена. Задача состоит в максимизации дисконтированной прибыли за период времени Т.

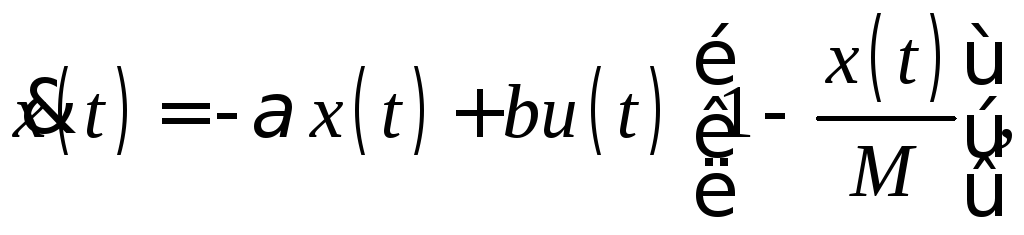
где – объем продаж в единицу времени;– уровень рекламной деятельности; М – емкость рынка;– заданные положительные параметры;– начальный и конечный моменты времени соответственно;– показатель скорости продаж,– эффективности рекламной деятельности;– начальный объем продаж; А – максимальный уровень рекламной деятельности;– дисконтирующий множитель; р – некоторая условная характеристика.

3. Оптимальное управление выпуском продукции с учетом вредных выбросов.

Пусть − капитал;− объем загрязнения;− объем выпуска продукции;,− доли выпуска продукции на потребление и борьбу с загрязнением соответственно.

Динамика роста капитала и загрязнения описывается уравнениями

,

,

где − доля выбытия капитала;− удельное загрязнение (ед. продукции);− скорость очистки.

Ставится задача максимизации функции полезности от выпускаемой продукции с учетом отрицательного влияния загрязнения:

.

Ограничения на управляющие параметры

, ,.

Числовые значения параметров: ;;.

Начальные условия задать самостоятельно. Определить, какие дополнительные условия необходимо задать для данной модели.

4. Исследование двухкамерной модели поглощения лекарства и метаболизма.

Двухкамерная модель поглощения лекарства и метаболизма может быть описана уравнениями

,

,

, ,

.

Здесь − масса лекарства в желудочно-кишечном тракте;− масса лекарства в крови;− количество принимаемых лекарств (управление);,− постоянные.

Целью управления является достижение желаемого количества лекарств в крови за минимально возможное время T.

5. Оптимальное управление в модели Лотки-Вольтерра с учетом потребности в пище для каждой популяции.

,

,

где и– число жертв и хищников в единицу времени соответственно;

описывает скорость прироста числа жертв в отсутствии хищников; − естественное вымирание хищников, лишенных пищи;,− положительны постоянные, характеризующие потребность в пище для каждой популяции (жертвы и хищника).

Хищники питаются в основном жертвами, среда ограничена.

−отлов, : здесь− часть отлова.

, ,,− заданы,,.

Требуется найти максимум функционала

,

где − стоимость,;− стоимость усилия,;,− заданные параметры задачи,.

6. Оптимальное управление в модели “хищник-жертва” с учетом внутривидовой конкуренции.

,

,

где и– число жертв и хищников в единицу времени соответственно;описывает скорость прироста числа жертв в отсутствии хищников;− естественное вымирание хищников, лишенных пищи;,− положительны постоянные, характеризующие потребность в пище для каждой популяции (жертвы и хищника).

Хищники питаются в основном жертвами, среда ограничена.

−отлов, : здесь− часть отлова.

, ,,− заданы,,.

−демпфирующий член, выражает подавляющее действие, которое данный вид оказывает на собственный рост в результате внутривидовой конкуренции.

Требуется найти максимум функционала

,

где − стоимость,;− стоимость усилия,;,− заданные параметры задачи,.

7. Модели хищник–жертва с запаздыванием.

Введем следующие обозначения: – численность жертв в момент времени,– численность хищников в момент времени,– управление, количество отловленных жертв в единицу времени,– управление, количество отловленных хищников в единицу времени. Модель хищник–жертва описывается системой дифференциальных уравнений с запаздыванием

,

начальные условия заданы на интервале запаздывания непрерывными функциями :

, ,.

Рассматривается два типа управления отловом популяции:

, ;
.

Здесь – заданная максимальная скорость отлова в-той популяции,– максимальная суммарная скорость отлова,– естественная скорость прироста числа жертв в отсутствии хищника,− естественное вымирание хищников, лишенных пищи (жертв), заметим, что эти параметры могут зависеть от времени,, характеризуют потребность в пище и пространстве,, – время взросления жертв и хищников соответственно. Процесс рассматривается на фиксированном отрезке времени. Заметим, что если,,, тоесть скорость отлова популяции. Если,,, то отловпоказывает, какая часть популяции отлавливается в момент времени.

Рассматриваемая управляемая модель относится к типу задач об использовании и сохранении природных ресурсов, в которой необходимо найти оптимальное управление, обеспечивающее наибольшую прибыль и сохранение численности популяций на заданном уровне ,.

Целью управления является максимизация функционала

,

где – стоимость жертв;– стоимость хищников;– стоимость оборудования для отлова жертв;– стоимость оборудования для отлова хищников;,, – стоимость популяций в момент времени;,, – желаемая численность в конечный момент времени. Заметим, что стоимость популяции в общем случае может зависеть от её численности, т. е.,, например, монотонно убывая с ростом популяции, а стоимость отлова возрастает с увеличением интенсивности отлова, а также зависит от времени (сезона отлова). В работе рассмотрен случай, когда эти величины принимают постоянные значения.

8. Модель оптимального управления процессом рыбной ловли.

Рассмотрим популяцию рыб, в которой в зависимости от веса, размера и способности приносить потомство выделено 3 возрастных класса. Изменение численности рыб 3-х классов описывается дифференциальными уравнениями:

,

где – количество рыб в-ом классе в момент времени;– коэффициент рождаемости;,– коэффициенты, характеризующие количество рожденных рыб, погибшее в результате конкуренции с рыбой-го класса (соревновательные факторы);,– коэффициенты естественной смертности рыб-го класса;– время взросления рыбы 1-го и 2-го классов соответственно и перехода в следующий класс;– коэффициенты, отражающий эффективность отлова рыб 2 и 3 классов;– усилие, прикладываемое для отлова рыбы, удовлетворяющее ограничению:

Первое уравнение представленной задачи описывает динамику изменения количества молодой рыбы (класс 1), второе уравнение – средней рыбы (класс 2), третье уравнение – взрослой рыбы (класс 3).

Введем новую переменную – объем рыбы, выловленной на момент времени, которая удовлетворяет следующим условиям:

Требуется выбрать управление, доставляющее минимум функционала:

где – дисконтирующий множитель;– средние стоимости одной рыбы 2-го и 3-го класса соответственно;– стоимость отлова рыбы в единицу времени;,– некоторые большие положительные числа;– желаемое количество рыбы каждого класса в момент времени;– величина спроса на данный вид рыбы на рынке потребления.

9. Моделирование распространения заболевания в однородном сообществе.

Обозначим через соответственно число людей, подверженных заболеванию, инфицированных и выздоравливающих. Пусть функцияхарактеризует число встреч людей подверженных заболеванию (класс 1), и инфицированных людей (класс 2). Свойства этой функции будут описаны ниже. Функциювыбирают в видеили. Здесьесть вероятность того, что человек из группы 1 встречает человека группы 2, при этом величинаесть вероятность того, что встреченный им человек принадлежит ко второй группе.

Динамика процесса распространения эпидемии описывается следующей системой дифференциальных уравнений:

здесь означает относительную скорость выздоровления,,− известные значения в начальный момент времени. Слагаемоев формулах выражает число людей, которые имеют иммунитет или выздоравливают в результате какого-либо иного процесса, величинаможет изменяться от 10 дней (ангина, простуда) до нескольких недель (холера, малярия) или даже месяцев и лет (до 18 лет AIDS).

В общем случае функция обладает следующими свойствами:

если х или у равны нулю; ; если

Заметим, что Если людям, подверженным заболеванию, вводится вакцина, то первое уравнение должно быть заменено уравнением

Из-за недостаточных технических и финансовых возможностей скорость введения вакцины ограничена, т.е. функция управления удовлетворяет неравенству

где характеризует максимальное число людей, которым может быть введена вакцина в единицу времени.

Стоимость заболевания складывается из цены ухода за инфицированными людьми и затрат на вакцину и ее введение. Принимая стоимость ухода за больными равной единице, запишем общую стоимость эпидемии за фиксированное время Т:

Обычно относительная стоимость вакцинации достаточно мала,

10. Оптимальное управление процессом распространения эпидемии в неоднородном сообществе.

Будем рассматривать неоднородное сообщество, состоящее из n социальных групп. Обозначим через x_i(t) – число подверженных заболеванию группе i и y_i(t) – число инфицированных людей группе i в момент времени t. Пусть функция f(x_i,y_j)=x_iy_j характеризует число встреч подверженных заболеванию в i-той группе, и инфициро­ванных людей в j-той группе, - коэффициент, характеризующий частоту встреч подверженных заболеванию в i-той группе и инфицированных людей в j-той группе.

Динамика процесса распространения эпидемии в неоднородном обществе, состоящем из n групп, описывается следующей системой дифференциальных уравнений:

, ,,

где скорость изменения числа подверженных заболеванию в i-той группе;скорость изменения числа инфицированных в i-той группе;

число заразившихся в i-той группе от инфицированного j-той группы с учётом того, что заражение могло произойти от инфицированного из любой j-той группы (); количество людей, восстановивших своё здоровье в i-той социальной группе без воздействия внешних средств: карантина, вакцинации и др. ( среднее время естественного выздоровления);  коэффициент, характеризующий частоту встреч здоровых людей i-той социальной группы с инфицированными людьми j-той социальной группы (в общем случае он может рассматриваться как функция ); коэффициент смертности людей в i-той группе, не связанной с болезнью;  коэффициент смертности от данной инфекции в i-той группе;  средняя скорость рождаемости в i-той группе.

Заметим, что x_i(t)+y_i(t) = const, x_i(0) и y_i(0) - известные значения в начальный момент времени.

Управлять процессом распространения эпидемии будем с помощью введения карантина, вакцинации и проведением информационно-образовательной программы «Здоровье». Обозначим  доля больных, отправленных на карантин,  доля вакцинированных среди подверженных заболеванию,  доля людей, подверженных заболеванию, на которых воздействовали с помощью программы «Здоровье». Тогда динамические уравнения примут вид:

Функционал:

характеризует цель управления, которая состоит в том, чтобы минимизировать затраты на лечение, где d_i – относительная стоимость вакцинации, - относительная стоимость программы «Здоровье», а c_i – относительная стоимость карантина в i-той группе (стоимость лечения инфицированного человека примем за единицу).

Ограничения на функцию управления заданы в следующем виде:

,
Начальные условия: ,.

11. Управление процессом распространения заболевания с помощью введения карантина.

При некоторых тяжелых заболеваниях контроль за процессом распространения эпидемии осуществляется с помощью изоляции инфицированных людей. Обычно в этом случае число инфицированных людей много меньше общего числа населения, т.е. идо тех пор, пока х не сравнимо с у. Предположим, что карантин не используется для изоляции людей с неизвестным состоянием, а вводится только в случае, если человек заболел. Модель динамики заболевания может быть представлена следующей системой дифференциальных уравнений:

где функция обладает следующими свойствами:

- среднее время заболевания. Цена заболевания выражается интегралом

Цена ухода за инфицированным человеком, находящимся на карантине, больше, чем за инфицированным человеком и, в этом случае

Если , то исходная задача может быть сведена к задаче:

12. Оптимальное управление развитием капитала с нелинейным функционалом.

Рассмотрим модель Солоу, которая определяет динамику роста капитала в зависимости от уровня потребления:

, где ;– коэффициент амортизации;– темп прироста трудовых ресурсов;– доля капитала от выпуска.

В качестве управления выберем потребление , которое удовлетворяет ограничению.

Максимизируем функцию полезности за период :

.

13. Оптимальное управление трехотраслевой экономикой.

Рассмотрим следующую экономическую модель. Будем считать, что одна отрасль (первая) производит средства производства, которые могу расходоваться на развитие трех отраслей. Две другие отрасли будем считать потребительскими. Обозначим через ,, мощность i-ой отрасли в момент времени t. Развитие экономики опишем следующим образом

,

где − доля продукта, которая поступает на развитие i-ой отрасли в момент времени t.

Введем ограничение ,,,

которое означает, что продукт используется целиком.

Будем считать, что начальные условия имеют вид

, ,.

Эти условия означают, что в первой отрасли начальная мощность равна единице, а во второй и третьей отраслях – нулю.

Используем в качестве критериев линейную комбинацию в конечный момент времени. Неотрицательные параметрыибудут определять приоритеты соответствующих отраслей.

14. Модель оптимизации финансовых процессов в условиях кризисных ситуаций.

Одним из основных аспектов общего экономического кризиса в России является финансовый кризис предприятий промышленности. Его характерными внешними признаками являются:

− накопление у предприятий и организаций большой кредиторской задолженности перед поставщиками продукции и услуг, бюджетами различных уровней и внебюджетными фондами;

− приостановка текущих платежей предприятий;

− отсутствие финансовых средств для обеспечения нормального производственного цикла.

Следствием этого являются спад промышленного производства и невозможность продолжения нормального функционирования предприятия промышленного комплекса.

В связи с этим возникает актуальная задача отыскания оптимальных стратегий функционирования предприятия в кризисных условиях, позволяющих вывести его из кризисного состояния на нормальный режим производства.

Очевидно, что для решения подобного рода задачи традиционные методы финансового анализа, основанные на статических моделях предприятия, неприменимы, так как понятие «оптимальность» стратегии предполагает наличие положительного долгосрочного эффекта, для определения которого необходимо прогнозирование как динамики показателей функционирования предприятии, так и параметров связанных с ним рынков.

Для проведения прогнозирования параметров предприятия необходимо использовать динамическую модель, описывающую его функционирование в кризисных условиях.

Рассмотрим динамическую модель функционирования предприятия в кризисных условиях, в которой учитывается наличие краткосрочной дебиторской и кредиторской задолженности в форме неплатежей за поставленные услуги и продукцию, а также штрафных санкций (штрафов, пени) за просроченную задолженность.

В модели рассматривается предприятие, производящее единственный вид продукции и реализующее его на рынке по цене l(t) (ден.ед/ед.прод). Для обеспечения процесса производства используются сырье и материалы, приобретаемые у поставщиков по ценам l_j . При этом предполагается, что количество работающих и производственная мощность предприятия постоянны на рассматриваемом промежутке времени.

Технология производства продукции описывается вектором технологических коэффициентов , (>0), определяющих расход сырья на единицу выпускаемого продукта в натуральном выражении, и функцией издержек(ден.ед/ед.времени), в которую включаются затраты, не связанные с закупкой сырья. В работе изучается случай возрастающей вогнутой функции, что соответствует технологии производства с возрастающими доходами на масштаб. Однако возможен случай рассмотрения линейной функции.

Выплаты производятся из средств предприятия (расчетный счет) (ден.ед), динамика которых определяется следующим образом:

; .

Здесь – величина спроса на продукцию предприятия в момент времениt (ед.прод/ед.ремени), – объем валового выпуска отрасли на момент времениt (ед.прод/ед.времени); – величина выплат по погашению задолженности на момент времениt (ден.ед/ед.времени).

Величина валовой задолженности (ден.ед) определяется следующим образом:

; .

Здесь – норма начислений на просроченную задолженность в момент времениt (%).

Уровень продаж ограничен запасом готовой продукции (ед.прод), изменение которого имеет вид

; ,

где – скорость потери запаса готовой продукции в единицу времени (% /единицу времени).

Предполагается, что объем выпуска ограничен имеющимися производственными мощностями , выплаты ограничены максимальной величиной выплат, величины счета, задолженности и объем запасов неотрицательны, наналожены условия, связанные с ограниченностью складских помещений:

.

В качестве цели функционирования рассматриваются с одной стороны, максимизация собственных средств предприятия , а с другой – минимизация величины задолженности. Критерий предприятия записывается в виде свертки данных целей с весамии, характеризующими их важность:

.

Заметим, что по смыслу задачи

,.

15. .Задача о построении поверхности вращения, обладающей максимальной площадью поверхности, с заданными ограничениями на ширину.

Задачи о построении оптимальных поверхностей состоят в нахождении поверхностей и тел, имеющих максимальную или минимальную площадь поверхности либо максимальный или минимальный объём при заданных ограничениях. Подобные задачи имеют широкую область приложений не только в самой геометрии, но и в других науках, а также практическое применение. Они возникают в задачах упаковки тел и раскроя. Эти задачи могут быть формализованы как задачи оптимального управления с фазовыми ограничениями типа равенств и неравенств. Аналитические методы вариационного исчисления предполагают условия гладкости на функции, используемые при формализации задачи, и в связи с этим не могут использоваться при решении подобных задач. Методы математической теории оптимального управления, в частности двойственный метод, позволяют преодолевать указанные трудности. В данной работе решена задача по построению выпуклой центрально-симметричной поверхности с заданными ограничениями на ширину, которая обладает максимальной площадью поверхности.

Ограниченную выпуклую пространственную фигуру будем описывать с помощью ее опорной функции, которая определяется равенством

где – единичный вектор направления. В сферической системе координатn имеет следующие компоненты: .

Определение 1. Плоскость назовём опорной плоскостью для множестваF в направлении . Обозначим черезС геометрической точки зренияесть расстояние от начала координат до опорной плоскости.

Определение 2. Если опорная плоскость имеет только одну общую точку с множеством F, то она является регулярной. Если все опорные плоскости множества F регулярны, то такое множество называется регулярным множеством или овалоидом, а его опорная функция – регулярной.

В случае регулярной фигуры ее опорная функцияпочти всюду вудовлетворяет условиям

где

(1)

Верно и обратное: любая -периодическая функция, удовлетворяющая условиям (1) и граничным условиямоднозначно определяет выпуклое регулярное множество. Нерегулярное множество не может быть описано с помощью условий (1), однако его опорная функция может быть равномерно аппроксимирована последовательностью опорных функций регулярных множеств.

Определение 3. Шириной выпуклого множества в направлении назовём функциюB()=H()+H(-).

Площадь поверхности выпуклой фигуры может определяется с помощью равенства

(2)

Не ограничивая общности, выберем начало координат так, чтобы в направлении фигура имела минимальную ширину, а начало сферической системы координат выберем так, чтобы опорная функция удовлетворяла следующим граничным условиям:

Рассматривается центрально-симметричная фигура вращения. В этом случае задача о нахождении фигуры максимальной площади поверхности с заданными ограничениями на ширину формализуется следующим образом.

Требуется найти выпуклую фигуру вращения максимальной площади поверхности

,

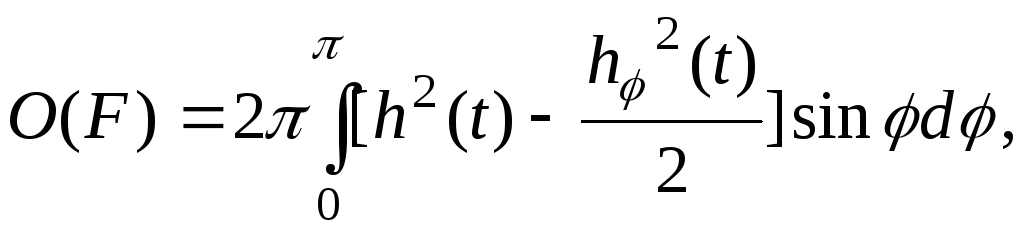опорная функция которой удовлетворяет условиям:

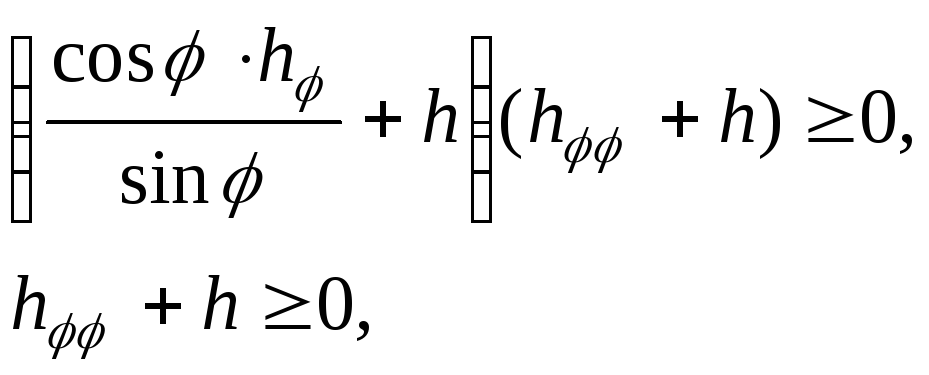
Введем функции и обозначим независимую переменную через.

В новых обозначениях задача является одномерной задачей оптимального управления с фазовыми ограничениями:

16. .Оптимальный контроль над загрязнением окружающей среды с помощью процессов очистки.

Любая производственная деятельность связана с воздействием на окружающую среду. Вопрос лишь в том, что такое воздействие может быть большим или меньшим. Наряду с тем, что производство различных товаров приводит к неодинаковому загрязнению, сами масштабы вредного воздействия могут быть сокращены, если производитель предпринимает какие-то меры по борьбе с ним. С точки зрения экономики производственный процесс приводит к возникновению издержек двух видов: с одной стороны, это экономический ущерб, вызываемый выбросами вредных веществ в окружающую среду, с другой – издержки предотвращения загрязнения, т. е. затраты на реализацию природоохранных мероприятий. Экономя на природоохранных затратах, мы терпим убытки из-за того, что природа стала хуже. Предотвращая ущерб, мы несем затраты по природоохранной деятельности. С точки зрения экономиста, необходимо научиться отвечать на вопрос, каково рациональное соотношение двух видов затрат. Именно эта проблема затрагивается в данной работе.

Исследуется модель контроля над запасами загрязнения с помощью процессов очистки. В качестве двух факторов производства рассматриваются трудовые ресурсы и основной капитал. Считаем, что предложение трудовых ресурсов не изменяется во времени. Особенность модели заключается в том, что выпуск может быть использован не только на накопление капитала и потребление, но и на борьбу с загрязнением. Предполагается, что полезные расходы на очистку используются для борьбы с широким набором загрязнителей. Этой модели соответствует, например, контроль над загрязнением вод.

Пусть производственная функция удовлетворяет обычным условиям вогнутости. Поскольку трудовые ресурсы фиксированы, это означает, что выпуск есть возрастающая функция от основного капитала. Положим, что – основной капитал предприятия к моменту времени. Определим производственную функцию в виде. Будем считать, что основной капитал убывает с фиксированной скоростью.

Через обозначим запас загрязнителя, накопленный в связи с деятельностью данного предприятия, к моменту времени. В этой модели загрязнитель не используется как полезный продукт. Предполагается, что его поток является побочным продуктом и пропорционален ему; продукты производства и загрязнитель связаны друг с другом. Под эту схему подходят сыворотка на молочном заводе, отходы предприятий, которые производят расфасовку мяса, органические остатки, получающиеся при изготовлении бумаги, и т.д. Соотношения между продуктом и загрязнителем дают нам возможность измерять загрязнение в тех же единицах, что и основную продукцию.

Эмпирические наблюдения показывают, что запас загрязнителей частично убывает естественным образом. Скорость очистки предполагается неотрицательной. Существует другой способ уменьшения загрязнения, а именно произвести определенные затраты на борьбу с загрязнением. Предполагается, что производительность затрат на борьбу с загрязнением постоянна. Расход единицы продукции уменьшает загрязнение наединиц.

Пусть и– неотрицательные доли выпуска, израсходованные на потребление и борьбу с загрязнением, так что поток потребленияравен. Скорость роста основного капитала имеет вид.

Скорость роста загрязнения будет равна . Предполагается, что как основной капитал, так и запас загрязнителя не могут быть отрицательными.

Целевую функцию определим с точки зрения всего общества. Благосостояние общества в любой момент времени есть функция от потребления и запаса загрязнения. Для простоты мы будем предполагать, что потребление и загрязнение входят в функцию полезности раздельно. Эта функция возрастает пои убывает по, т. е.. Предполагается также, чтои. Очевидно, что рост потребляемых благ неодинаково влияет на рост функции полезности. Первые порции продукции приносят больше удовольствия, чем последующие, т. е. происходит некоторое насыщение продуктом. Следует также учесть, что изначально запас загрязнения невелик, а при увеличении запаса загрязнения функция полезности начинает убывать все быстрее. Таким образом, мы полагаем, что. Определим не зависящую от времени функцию полезности следующим образом:

.

Поток полезности оценивается с учетом субъективной скорости дисконтирования . Общее благосостояние получается суммированием дисконтированных потоков и имеет вид

.

Математическая формулировка задачи. Необходимые условия оптимальности.

Требуется минимизировать функционал

при динамических условиях, заданных системой дифференциальных уравнений

с начальными условиями

,

с фазовыми ограничениями

,

с ограничениями на управление

.

Здесь – абсолютно непрерывная на отрезкефункция состояния,– кусочно-непрерывная на отрезкефункция управления.

17. Оптимальное управление температурным режимом помещения.

Будем рассматривать модель оптимального управления температурным режимом помещения. Данная модель может найти практическое применение для решения задачи соблюдения оптимального температурного режима, в таких помещениях как хранилища библиотечных фондов, музейные запасники, зерно- и овощехранилища, инкубаторы, операционные, лаборатории, производящие лекарственные препараты, сыворотки, вакцины и т.д. Во всех перечисленных случаях важнейшим фактором служат естественные и создаваемые искусственно условия среды хранения. Основной показатель внешней среды – это воздух с его физическими свойствами, постоянными химическим составом частей и посторонними газами, механическими примесями и микрофлорой. Температурный показатель является наиболее важным, так как во многом определяет остальные. Поэтому важно уметь поддерживать его оптимальные значения.

Рассмотрим процесс изменения температуры в помещении с двумя смежными комнатами и нагревателем (кондиционером), расположенным в первой из них. Обозначим через и- температуры, ат₁ и т₂ – массы воздуха в первой и второй комнатах соответственно; k₁ – коэффициент теплообмена между комнатами; k – число, характеризующее потери за счет конвекции ;с – теплоемкость воздуха; А – температура наружного воздуха; - управление количеством теплоты, выделяемым нагревателем, расположенным в первой комнате.

Температуру в комнатах и температуру наружного воздуха будем измерять в Кельвинах (К); массу воздуха – в килограммах (кг); управление, выражающее количество теплоты в единицу времени, − в ваттах ; − характеризует изменение температуры воздуха в комнате в единицу времени и измеряется в .

Пусть требуется нагреть первую комнату до температуры В₁, а вторую комнату до температуры В₂ за заданное время при минимальных расходах на управление. Введем коэффициенты приоритета .

Математическая модель управляемого процесса может быть представлена в виде следующей задачи оптимального управления. Требуется найти минимум функционала

(1)

при динамических ограничениях

	(2)
	(3)

начальных условиях

(4)

и ограничении на управление

.

(5)

В вычислительных экспериментах можно использовать формулы, выражающие известные физические закономерности и соотношения. Так температура воздуха переводится из шкалы Цельсия в шкалу Кельвина и обратно с помощью соотношения .

Масса воздуха в комнатах вычисляется по формуле , где− плотность воздуха,V – объем, занимаемый воздухом (объем комнаты), плотность воздуха равна 1.29 кг/м³. Считая воздух двухатомным газом, а давление постоянным, согласно классической теории теплоемкости, вычислим теплоемкость по формуле , где− средний молекулярный вес воздуха, аR – универсальная газовая постоянная. Известно, что кг/моль,R=8.31441 Дж/(К•моль). Поэтому размерность с равна Дж/(Ккг). Легко проверить, что размерности левых и правых частей уравнений (2) − (3) совпадают.

18. Оптимальное управление запасами однородной продукции.

Рассмотрим непрерывную модель управления запасами однородной продукции, когда известен начальный уровень запасов, мощность производства, восстанавливающего запасы, и спрос на продукцию.

Пусть – уровень запасов;– объем производства;– цена производства;с – цена хранения продукции; – спрос на продукцию.

Динамика изменения уровня запасов:

.

Мощность ограничивает объем производства

.

Необходимо минимизировать затраты на производство и хранение продукции, объем которой отклоняется от планового уровня объема производства и планового уровня запасовза времяТ, регулируя уровень производства продукции , т.е.

.

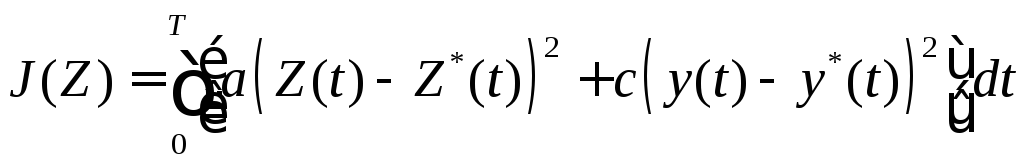В качестве одного из примеров возьмем следующие значения параметров: ;;;;;;.

19. Оптимальное управление процессом производства, хранения, реализации товара.

На предприятии производится товар. Произведенный товар поступает для продажи. Скорость продажи зависит от условий продажи и состояния рынка. Товар, хранящийся на рынке, подвержен порче, вследствие чего его количество при хранении уменьшается. Кроме того за хранение товара необходимо платить. В модели рассматривается товар, который по истечении гарантийного срока хранения направляется в перепроизводство (это характерно, к примеру, для хлебной промышленности). Прибыль от выпуска товара определяется как разность полученной от продажи выручки и затрат на производство и хранение товара.

Введем следующие обозначения: − количество товара, произведенного в момент времени,− количество товара (продукта) на руках у потребителей в момент времени,− величина, характеризующая цену товара в момент времени, причем цена ограничена;− темп потребления товара;− потенциальный спрос, то есть количество товара, необходимое для полного насыщения рынка,;γ – темп роста производства, ;− коэффициент скорости продаж, который определяется как отношение количества проданного товара к общему числу товара,.

Естественно предположить, что скорость изменения количества товара на руках у потребителей пропорциональна количеству производимого товара с коэффициентом пропорциональности , зависящим от разных факторов. Будем считать, чтозависит от величины, характеризующей цену товара, от потребительской способности рынка и от коэффициента скорости продаж. Потребительская способность рынка может быть выражена как потребность в товаре:. Зависимость коэффициента,,,) различна для разных видов товара. Например, для товаров длительного пользования этот коэффициент стремится к нулю, для быстро потребляемых товаров, например, продуктов питания, спрос всегда существует независимо от количества проданного товара. Изменение количества товара на руках у потребителей описывается уравнением

,

где коэффициент пропорциональности определяется как

,

а второе слагаемое означает, что происходит уменьшение количества товара на руках у потребителей за счет его потребления.

Будем полагать, что количество произведенного товара уменьшается на ту же величину, на которую увеличивается количества товара на руках у потребителей. Скорость изменения количества производимого товара зависит также от темпа роста производства. При этих допущениях получаем уравнение, описывающее изменение количества производимого товара.

.

Прибыль от выпуска товара определяется как разность выручки , полученной от продажи, и затрат на производствои хранение товара. С учетом баланса расходов и доходов, прибыль, получаемую за период времени, можно оценить выражением, которое требуется максимизировать

,

где − дисконтирующий сомножитель, выражающий тот факт, что деньги со временем девальвируются. Терминальное слагаемое отвечает за величину прибыли от товара, гарантийный срок хранения которого истек (продукт может быть, к примеру, направлен на перепроизводство).

Предположим, что цена за хранение единицы товара в единицу времени составляет единиц цены, а за производство −единиц, тогда функцииможно взять в виде:

где − цена реализации остатка товара, а− коэффициент, отвечающий за вложение предприятием средств в расширение производства.

Будем измерять количество товара (продукта) в а время – вТогда,иизмеряются в,,− в ()^-1, как и− в()^-1, − в ()^-1, − в ()^-1, и функционал – безразмерные величины. Умножив функционал на некоторую константу с – нормировочный коэффициент денежной размерности, получим значение функционала в денежном эквиваленте.

Математическая модель управляемого процесса может быть представлена в виде следующей задачи оптимального управления. Требуется найти минимум функционала

,

(1)

при динамических ограничениях

,	(2)
	(3)
начальных условиях	(4)

и ограничениях на управление

, .

(5)

Далее будем полагать, что .

20. Оптимальная стратегия производства товара длительного пользования при нелинейном спросе.

Рассмотрим модель создания производства товара длительного пользования, позволяющая выбирать рациональную стратегию развития новой отрасли народного хозяйства.

В основе модели лежат следующие предпосылки. Производство направлено на выпуск нового типа продукта. В разные годы это могли быть телевизоры, холодильники, персональные компьютеры и т.п. Имеющаяся инфор­мация о данном товаре и наличие его у некоторых индивидуумов (например, если его привезли из-за границы) могут до создания соответствующего производства привести к формированию ненулевого спроса.

Одним из наиболее сильных ограничений в модели является предположение о том, что функция спроса на новый товар известна. Точнее, полагается известной “базовая” функция спроса −количество товара, которое население готово купить в году i по цене p, если в начале периода ни у кого его не было. Считается, кроме того, что при фиксированной цене “базовый” спрос не убывает со временем. Остановимся на формальной стороне построения модели.

Пусть − коэффициент выбытия нового товара, a − количество продукта, находящегося в периодk в пользовании той части населения, которая в момент i, i>k, готова купить его по цене р. Тогда фактический спрос вi зависит от p¹, ..., pⁱ − цен предыдущего и настоящего времени и равен .

Считая, что изменение спроса со временем происходит только за счет вовлечения на рынок новых потребителей, не высказывавших ранее желание купить новый товар, и что те, кто хотел его приобрести по цене р в момент i, готовы купить его и позже по цене , можно приближенно оценить фактический спрос

(1)

Вместо фактического спроса всюду будем рассматривать его приближениеDⁱ, определяемое в (1). В дальнейшем, говоря о текущем спросе, будем иметь в виду Dⁱ_.

Если − строго монотонная по р функция, то существует обратная функция спроса gⁱ(q), определяющая цены р, при которых в момент i найдется q желающих купить новый товар в ситуации, когда его ни у кого прежде не было. Считается, что убывает с ростом р.

При создании и функционировании отрасли используются имеющиеся ресурсы. Объем годового производства ограничен в каждом году i мощностями Mⁱ и теку­щим спросом Dⁱ.

Новые мощности и новый товар имеют конечные сроки службы, задаваемые с помощью коэффициентов выбытия.

Выбор оптимальной стратегии при создании новой отрасли предлагается де­лать в соответствии с решением следующей задачи

(2)

Здесь k⁰, q₀ – заданы; λ< 1 – дисконт; Mⁱ – мощность новой отрасли в году i, – коэффициент годового выбытия производственных фондов;kⁱ – объем ввода новых мощностей в году i; cⁱ – условно-постоянные затраты на единицу производственных мощностей; rⁱ – стоимость набора инвестиционных ресурсов, затрачиваемых в году i для ввода единицы производственных мощностей.

Искомые параметры q_i , kⁱ , Mⁱ , pⁱ , здесь Mⁱ – управление.

Более рассмотрим частный случай, когда не зависит от i и соответственно g(q, i) = p(q). Предполагается, что определяемая оптимальная мощность М вводится в начале планового периода и в дальнейшем не меняется, т.е. Mⁱ =M, kⁱ=0.

Основной гипотезой в модели является следующая: цены со временем не возрастают.

При ее выполнении и в предположении, что спрос не возрастает при повышении цены, из (1) получаем Тогда, положив =, r = 1−γ, c – удельные капитальные вложения, (2) можно переписать в виде

где q₀ – задано.

Цель: максимизация по q_i, М (максимально возможный выпуск нового продукта (мощность новой отрасли)) функции.

λ< 1 – дисконт,

g(q, t) = p(q),

–количество товара, которое население готово купить в году t по цене p, если в начале периода ни у кого его не было,

(– коэффициент выбытия нового товара),

М − максимально возможный выпуск нового продукта (мощность новой отрасли).

21. Задача оптимального управления с бюджетным ограничением.

Установление налоговой шкалы, удовлетворяющей определенным принципам и ограничениям, может быть сведено к решению некоторой задачи оптимального управления.

Задача оптимального управления с бюджетным ограничением для функции y

,

, ,

,

.

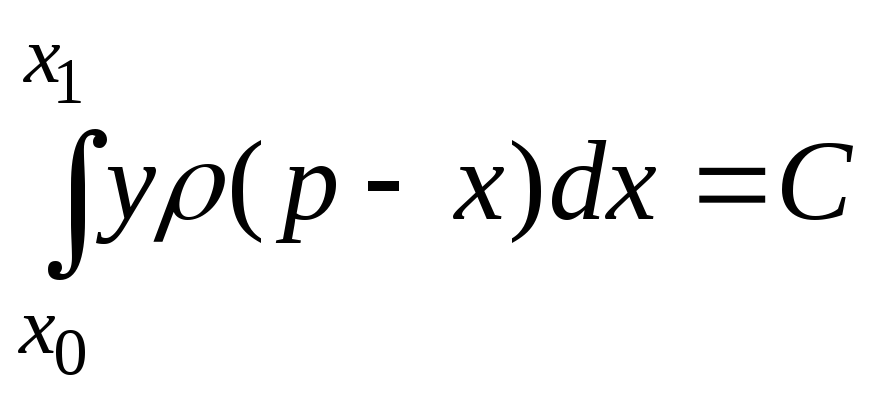Пусть y – налог на удельные затраты; x – независимая переменная, характеризующая удельные затраты того или иного производителя продукции, включенной в состав госзаказа; x₀–удельные затраты на выпуск аналогичной продукции на мировом рынке; x₁–удельные затраты, при которых предприятие еще целесообразно включать в число исполнителей госзаказа; p – цена единицы продукции, включенной в госзаказ, которая по тому же принципу исчисляется на основе мировых цен на соответствующую продукцию.

Также известен прогноз в отношении плотности размещения госзаказа, то есть экспертно найденная функция ,, характеризующая планируемое размещение заданного объема госзаказа на тех предприятиях чьи удельные затраты лежат в интервале , при этом она предполагается положительной и непрерывной.

22. Оптимальное управление квазилинейными системами.

Постановка задачи. Требуется найти минимум функционала, определенного на отрезке [0,T], где T – фиксировано, состоящего из интегрального и терминального слагаемых.

.

(1)

Динамические ограничения, заданы системой квазилинейных неоднородных уравнений

, ,

(2)

линейных фазовых ограничениях интегрального типа

,

(3)

и ограничениях на управление

почти всюду

(4)

Предположим, что является абсолютно непрерывной функцией на, а функция управления− кусочно-непрерывной. В данной задаче−n-мерный вектор, иматрицы размераисоответственно,− матрица размера.заданные вектора;− константы,−-мерная вектор-функция.

Для решения этой задачи введем новую фазовую функцию , следующего вида

где функция удовлетворяет системе дифференциальных уравнений

,

(5)

с начальным условием и ограничениям типа неравенств на правом конце траектории

.

(6)

В результате этого преобразования задача оптимального управления с фазовыми ограничениями интегрального типа (1) − (4) сводится к задаче оптимального управления с ограничениями типа неравенств (6) на правом конце.

Вид терминального ограничения позволяет сделать вывод, что в конечный момент времени выполняется одно из трех условий

,

Условия a) и b) соответствуют случаю закрепленного правого конца фазовой траектории условиеc) – случаю свободного правого конца. В результате получаем три задачи оптимального управления, которые различаются только условиями на правом конце.

23. Управление ростом биомассы путём изменения концентрации биогенов.

Широкое использование продукции из водорослей в различных отраслях промышленности − от медицинской до пищевой − повлекло за собой расширение их промысла. Наряду с коммерческой ценностью водоросли − важный компонент биоты, ежегодно образующий большое количество первичной продукции. Их заросли являются постоянной или временной экологической нишей для многих беспозвоночных и рыб, обеспечивая им благоприятные условия для размножения, убежище и пищу. Образуя плотные заросли в прибрежной полосе, водоросли служат естественным гасителем энергии волн, в результате снижают скорость разрушения берегов и замедляют относительно стабильные условия существования для прибрежной биоты.

Учитывая важное значение водорослей в экосистемах прибрежья, необходимо обратить особое внимание на проблему рациональной эксплуатации их зарослей. С экологической точки зрения понятие “рациональной эксплуатации биоресурсов” определяет осуществление промысла с учётом предельных объёмов изъятия промыслового объекта без разрушения, условия обеспечивающих возможность их полного восстановления и сохранения естественно сложившихся взаимосвязей всех компонентов экосистемы.

На рост водорослей оказывают влияние такие природные фактора как температура воды и воздуха, солёность воды, освещенность, концентрация биогенных элементов в среде.

Постановка задачи. Построим модель, описывающую процесс роста биомассы водоросли в зависимости от концентрации биогенов на интервале времени I = [0; T]. Пусть будет обозначать биомассу водоросли,обозначает производнуюпо времени.

Динамические ограничения, описывающие скорость изменения биомассы водоросли, будут следующими:

.

Ограничения на управление: .

Начальные условия:

обозначает концентрацию биогена в среде;

−некоторая максимальная концентрация биогенов в среде, после которой наступает перенасыщение;

−максимальная удельная скорость роста;

−константа полунасыщения для роста, т.е. концентрация биогена, при котором - удельная скорость роста;

−максимальная биомасса, достигаемая водорослями за рассматриваемый период.

Функционал

характеризует цель управления, которая состоит в том, чтобы максимизировать прибыль, полученную от реализации водорослей, где стоимость единицы биомассы водоросли,стоимость затрат, связанных с искусственным внесением биогенов,γ – стоимостная характеристика (характеризует стоимость биомассы (x(t)) в конечный момент времени T).

Для реализации задачи необходимо знать значение всех параметров. Основные биологические характеристики берутся из статистического анализа эмпирических данных. В гидробиологии для вычисления удельной скорости роста наиболее часто используется уравнение , гдеи- вес в начале и конце рассматриваемого периода. Данное уравнение было введено в биологию в 1927 г. Одновременно русским и американскими исследователями – И. И. Шмальгаузеном и С. Броди. Последний вывел это уравнение путём решения дифференциального уравненияпри предположении, что удельная скорость роста является константой и неизменна во времени. Исходя из понятия удельной скорости роста, можем вывести соотношение для константы полунасыщения и концентрации биогенов в среде:.

Данные начальной биомассы и максимальной биомассы, достигаемой водорослями за рассматриваемый период,получаем из эмпирических данных.

24. Модель вывода ракеты на заданную круговую орбиту.

Движение космического аппарата осуществляется при помощи системы управления, измеряющей параметры движения и вырабатывающей сигналы таким образом, что в соответствии с их величиной исполнительные и рулевые органы изменяют управляющие силы и моменты, обеспечивая движение космического аппарата.

Общую систему автоматического управления движения космического аппарата можно разделить на две практически независимые системы управления: систему управления движением центра масс космического аппарата (система навигации) и систему управления движением относительно центра масс космического аппарата (система ориентации).

Главными действующими силами являются силы тяготения Земли, кориолисовы силы от вращения Земли, сила тяги двигателей. Аэродинамические силы в космосе играют в большинстве случаев второстепенную роль. Поэтому в отличие от движения самолета в атмосфере, где для управления используются аэродинамические силы, в космических аппаратах управляющей силой является сила тяги двигателей. Изменяя величину и направление тяги двигателей, можно осуществить маневр космического аппарата в плоскости орбиты и менять эту плоскость, выполнить пространственный маневр, сближение с другим космическим аппаратом для перехвата или мягкого контакта, снижение в атмосфере, посадку на планету, лишенную атмосферы, и т.д.

К случайным воздействиям на космический аппарат можно отнести следующие факторы: влияние несферичности Земли и неоднородность ее массы, отклонения плотности атмосферы от стандартной, ошибки определения аэродинамических коэффициентов, вращение атмосферы вместе с планетой, случайные флюктуации ветра, влияние сил притяжения Солнца, Луны, планет, светового давления, электромагнитного поля и т.д.; ошибки чувствительных элементов и измерительных систем, ошибки преобразователей, случайное изменение массы космического аппарата и др. Наиболее существенными случайными воздействиями на управляемый аппарат являются флюктуации тяги двигателей и электронной аппаратуры системы управления.

Рассмотрим математическую модель, предназначенную для решения задач вывода космических кораблей на заданную круговую орбиту:

с граничными условиями

В данной модели приняты следующие допущения:

1. Космическую ракету и Землю можно считать материальными точками, подчиняющимися закону всемирного тяготения.

2. Земля неподвижна, т.е. пренебрегаем кориолисовыми силами.

3. Учитываются лишь сила тяготения Земли, сила сопротивления воздуха и сила тяги двигателя. Другие силы пренебрежимо малы.

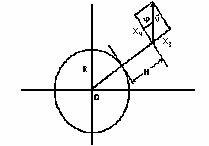
Рисунок 1

3. Управление движением центра тяжести ракеты осуществляется за счет изменения направления силы тяги двигателя, которая приложена к центру тяжести ракеты.

5. Закон управления должен обеспечивать движение ракеты в постоянной плоскости до выхода ракеты на заданную круговую орбиту.

6. Закон управления должен обеспечивать выход ракеты с минимальным расходом топлива, т.е. быть оптимальным по критерию минимума расхода топлива.

Рассмотрим физический смысл переменных в данной модели. Переменные (км) – высота полета космического аппарата над поверхностью Земли и (км) – горизонтальная дальность полета описывают положение космического аппарата в пространстве. Переменные (км/ч) – нормальная и тангенциальная составляющие вектора скорости космического аппарата, φ (рад) – угол между вектором скорости центра масс и горизонтом. Справедливо соотношение Пусть(т) – масса космического аппарата, тогда (т/ч) – скорость расхода массы. (т/км ч²) – коэффициент, характеризующий плотность атмосферы, поэтому (Н) – сила сопротивления воздуха (пропорциональна скорости космического аппарата); g (км/ч²) – сила тяготения Земли; (Н) – сила тяги двигателя; – управляющие функции;(т/ч) – секундный расход топлива; (рад) – программа поворота двигателей; (км/ч) – скорость истечения отбрасываемой массы по отношению к ракете (постоянная двигателя).

Для того чтобы движение спутника происходило по заданной круговой орбите, необходимо, чтобы скорость движения спутника в момент его выхода на орбиту равнялась теоретической скорости движения космического тела по указанной орбите. Эта теоретическая скорость находится по формуле

где ,R – радиус орбиты.

При этом вектор скорости должен быть направлен по касательной к орбите. Эти условия записываются в виде

Ясно, что сформулированным выше условиям за счет выбора управления можно удовлетворять различными способами, что создает возможность расчета управления, обеспечивающего оптимальную траекторию вывода спутника на орбиту при выборе соответствующего критерия оптимальности и решении оптимизационной задачи. В качестве критериев оптимальности обычно рассматривают минимум расхода топлива или минимальное время вывода спутника на заданную орбиту.

Следует заметить, что изложенная выше модель упрощена для облегчения возможности ее изучения. Реальные расчеты, безусловно, производятся при помощи более сложных моделей, учитывающих более точно и гораздо большее число факторов, влияющих на траекторию движения. Основой более сложных моделей является представленная модель.

Постановка задачи.

Требуется минимизировать функционал

(1)

при динамических условиях, заданных системой дифференциальных уравнений

	(2)
с граничными условиями	(3)
	(4)

и с ограничениями на управление

.

(5)

Здесь – абсолютно непрерывная на отрезке функция состояния,– кусочно-непрерывная на отрезке функция управления.

Отметим, что

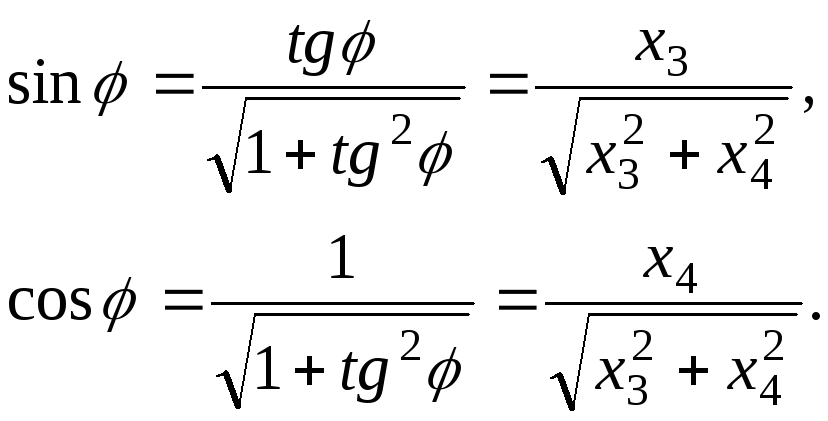
25. Решение экстремальных задач геометрии на плоскости.

Исследования свойств выпуклых фигур известны с глубокой древности. Все ученые, благодаря которым мы знаем геометрию в ее современном виде, так или иначе в своих трудах касались экстремальных свойств геометрических фигур. Одним из значительных вкладов в область исследования экстремальных свойств выпуклых фигур можно считать труды Вильгельма Бляшке. Он ставил перед собой разнообразнейшие задачи относительно круга, шара, тел вращения и их экстремальных свойств. Геометрические задачи ставили в своих работах И.М. Яглом, В.Г. Болтянский. Однако в то время в разнообразных исследованиях в области геометрии использовались в основном геометрические методы, что казалось вполне естественным.

Рассмотрим и формализуем следующие задачи:

− построение плоской выпуклой фигуры минимального периметра с ограничениями на ее ширину;

− построение плоской выпуклой фигуры максимальной (минимальной) площади с ограничениями на ее ширину.

Ограниченное замкнутое выпуклое множество будем описывать с помощью опорной функции этого множества. Пусть n – единичный вектор направления в пространстве .

Плоскость назовем опорной плоскостью для множестваF в направлении n, а функцию – опорной функцией множестваF в направлении n.

Введем полярные координаты в евклидовом пространстве , тогда. Положими назовем эту функцию опорной функцией множестваF в направлении . С геометрической точки зренияесть расстояние от начала координат до опорной прямой, соответствующей направлению(рисунок 1).

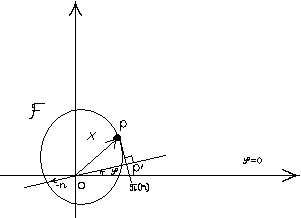
Рисунок 2

Если опорная плоскость имеет только одну общую точкуP с множеством F, то эта опорная плоскость является регулярной.

Если все опорные плоскости множества F регулярны, то назовем такое множество регулярным множеством, или овалом, а его опорную функцию – регулярной опорной функцией множества F.

Пусть P – точка касания опорной прямой выпуклого овала F.

Тогда ,.

Ширину выпуклого множества F в направлении определим как величину.

Диаметром выпуклого множества F назовем D=.

Ширина выпуклого множестваF определяется равенством .

Опорная функция овала почти всюду на отрезке удовлетворяет дифференциальному уравнению,, где– радиус кривизны границы овалав точке касанияP опорной прямой, соответствующей направлению . Это условие позволяет записать динамическую систему при формализации.

К поставленным задачам ранее уже был применен двойственный метод, позволяющий решать задачи с фазовыми ограничениями, и для них получены аналитические решения. Рассмотрим каждую из задач.

Задача о построении выпуклой фигуры минимального периметра.Рассмотрим данную задачу. Сначала получим выражение для периметра множества L(F) через функцию ширины этого множества. Используя определение периметра L(F), периодичность опорной функции и соотношения ,, получим. При этом если множествоF есть фигура постоянной ширины, т.е. , то.

Задачу построения выпуклой фигуры минимального периметра сведем к определению опорной функции этой фигуры или ее ширины.

Пусть – ширина фигуры в направлении t, положим по определению . Тогда, используя условие,, запишем требование выпуклости искомой фигуры,, где управление– кривизна фигуры.

Требуется построить выпуклую плоскую фигуру минимального периметра с ограничениями на ее ширину :,(ширина фигуры в направленииравна).

Данная задача может быть формализована как

при ограничениях:

,

,

,

,

,

,

.

94