
Практикум по элементарной математике (цвет)
.doc
Решение.
Если
![]() ,
то
,
то
![]() и неравенство системы предстает в виде
и неравенство системы предстает в виде
![]() .
Оно, а значит и сама система, действительных
решений не имеет. Следовательно,
.
Оно, а значит и сама система, действительных
решений не имеет. Следовательно,
![]() .
Тогда
.
Тогда
![]() и неравенство можно переписать в виде:
и неравенство можно переписать в виде:
![]() .
Далее рассмотрим два случая.
.
Далее рассмотрим два случая.
1)
Пусть
![]() .
Тогда
.
Тогда
![]() .
.
Найдем
корни уравнения
![]() :
:
![]() .
.
Решением
неравенства
![]() будет интервал
будет интервал

при
условии, что дискриминант
![]() .
По условию задачи этот интервал должен
содержать хотя бы одну точку
.
По условию задачи этот интервал должен
содержать хотя бы одну точку
![]() .
Так как
.
Так как
![]() ,
то условие задачи будет выполнено в том
и только том случае, когда
,
то условие задачи будет выполнено в том
и только том случае, когда

2)
Пусть
![]() .
Тогда
.
Тогда
![]() .
.
Решением
неравенства
![]() будет интервал
будет интервал

при
условии, что дискриминант
![]() .
Так как
.
Так как
![]() ,
то условие задачи будет выполнено в том
и только том случае, когда
,
то условие задачи будет выполнено в том
и только том случае, когда

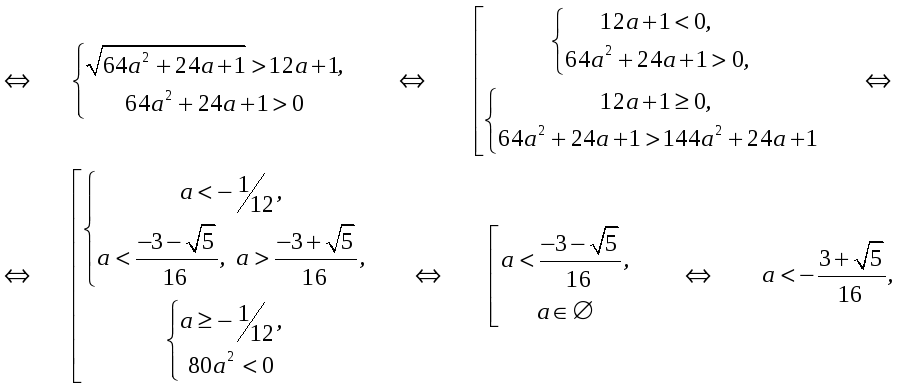
где
![]() - корни уравнения
- корни уравнения
![]() .
#
.
#
Замечание.
Геометрический смысл задачи состоит в
нахождении тех параметров
![]() ,
при которых парабола
,
при которых парабола
![]() пересекает внутренность окружности
пересекает внутренность окружности
![]() :
:


![]()
![]()




![]()


![]()

![]()
Пример
2. Найти
множество всех пар
![]() действительных чисел, для каждой из
которых равенство
действительных чисел, для каждой из
которых равенство
![]() верно для всех положительных чисел
верно для всех положительных чисел
![]() .
.
Решение.
Подставим в равенство
![]() три значения:
три значения:
![]() ,
,
![]() и
и
![]() .
Получим, соответственно, три равенства:
.
Получим, соответственно, три равенства:
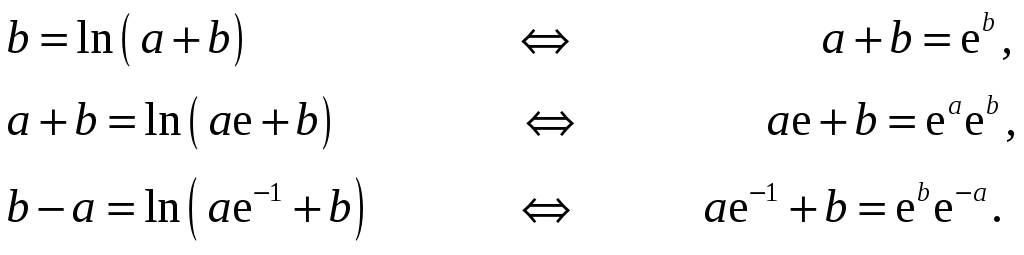
Составим
систему уравнений относительно
неизвестных
![]() и
и
![]() ,
возведя в квадрат первое равенство и
перемножив второе и третье:
,
возведя в квадрат первое равенство и
перемножив второе и третье:


Итак,
для того чтобы равенство
![]() выполнялось для значений
выполнялось для значений
![]() ,
,
![]() и
и
![]() ,
необходимо, чтобы
,
необходимо, чтобы
![]() и
и
![]() .
Осталось лишь убедиться, что при этих
значениях параметров
.
Осталось лишь убедиться, что при этих
значениях параметров
![]() и
и
![]() заданное равенство будет выполнено для
всех
заданное равенство будет выполнено для
всех
![]() .
Это действительно так, поскольку при
.
Это действительно так, поскольку при
![]() и
и
![]() исходное равенство является тождеством:
исходное равенство является тождеством:
![]() .
#
.
#
Найти
все числа
![]() ,
для каждого из которых система имеет
действительные решения:
,
для каждого из которых система имеет
действительные решения:
1)
 2)
2)
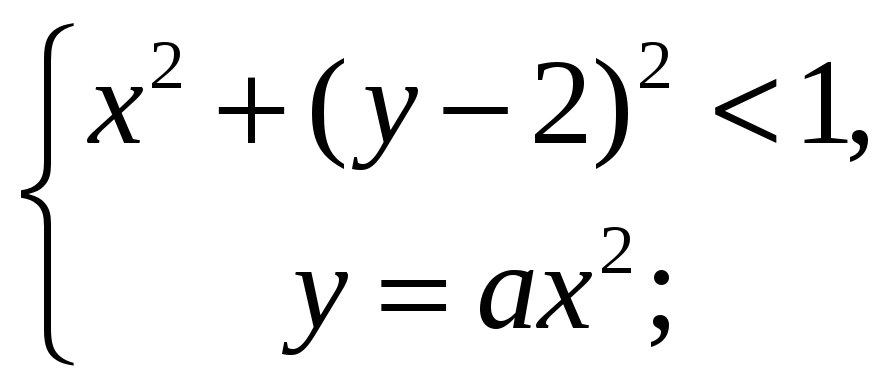 3)
3)
 4)
4)
 5)
5)
 6)
6)
 7)
7)

Найти
множество всех пар
![]() действительных чисел, для каждой из
которых при всех
действительных чисел, для каждой из
которых при всех
![]() верно равенство:
верно равенство:
8)
![]() ;
9)
;
9)
![]() ;
10)
;
10)
![]() .
.
Доказать,
что для всех действительных чисел
![]() и
и
![]() верно неравенство:
верно неравенство:
11)
![]() ;
12)
;
12)
![]() ;
13)
;
13)
![]() .
.
2) Во второй части задания содержатся задачи на пирамиды.
Пример
3. В правильной
четырехугольной пирамиде
![]() с вершиной
с вершиной
![]() все ребра равны
все ребра равны
![]() .
Через вершину
.
Через вершину
![]() и середины ребер
и середины ребер
![]() и
и
![]() проведена плоскость. Найдите площадь
и периметр сечения, отношение объемов
рассекаемых плоскостью частей пирамиды,
расстояние от вершины
проведена плоскость. Найдите площадь
и периметр сечения, отношение объемов
рассекаемых плоскостью частей пирамиды,
расстояние от вершины
![]() до секущей плоскости, а также угол между
плоскостью основания и секущей плоскостью.
до секущей плоскости, а также угол между
плоскостью основания и секущей плоскостью.
Решение.
Пусть
![]() и
и
![]() середины ребер
середины ребер
![]() и
и
![]() соответственно, а
соответственно, а
![]() - точка пересечения продолжений отрезков
- точка пересечения продолжений отрезков
![]() и
и
![]() .
Искомое сечение представляет собой
четырехугольник
.
Искомое сечение представляет собой
четырехугольник
![]() ,
где
,
где
![]() - точка пересечения отрезков
- точка пересечения отрезков
![]() и
и
![]() .
.
![]()






![]()









![]()
![]()




![]()



![]()
![]()
![]()




![]()
![]()

![]()
![]()

![]()
Поскольку
все боковые грани пирамиды являются
правильными треугольниками, то
![]() - это высота, медиана и биссектриса
- это высота, медиана и биссектриса
![]() .
Поэтому
.
Поэтому
![]() .
Далее заметим, что
.
Далее заметим, что
![]() ,
так что
,
так что
![]() и, значит,
и, значит,
![]() и
и
![]() - медианы
- медианы
![]() .
Следовательно,
.
Следовательно,
![]() и
и
![]() .
По теореме косинусов
.
По теореме косинусов
![]() .
Аналогично находим
.
Аналогично находим
![]() .
Наконец, по теореме Пифагора
.
Наконец, по теореме Пифагора
![]() ,
так что периметр
сечения
равен:
,
так что периметр
сечения
равен:
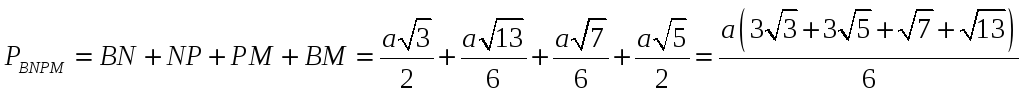 .
.
Для
вычисления площади
![]() применим формулу Герона:
применим формулу Герона:
![]() ,
где
,
где
![]() ,
,
![]() и
и
![]() - длины сторон
- длины сторон
![]() ,
а
,
а
![]() - его полупериметр. Так как
- его полупериметр. Так как
![]() и
и
![]() ,
то
,
то
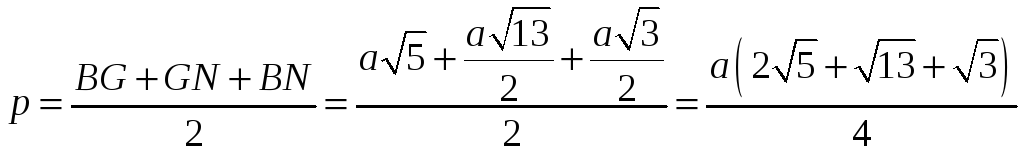 и
и

С
другой стороны,
![]() ,
поэтому
,
поэтому
![]() и, значит,
и, значит,
![]() .
Теперь
.
Теперь
![]() и
и
![]() -
-
величина искомой площади сечения.
Пусть
![]() и
и
![]() .
Так как пирамида
.
Так как пирамида
![]() - правильная, то
- правильная, то
![]() - высота пирамиды. Следовательно,
- высота пирамиды. Следовательно,
![]() - высота пирамиды
- высота пирамиды
![]() ,
а
,
а
![]() - высота пирамиды
- высота пирамиды
![]() ,
причем
,
причем
![]() (поскольку
(поскольку
![]() -
средняя линия
-
средняя линия
![]() ),
а
),
а
![]() (так как
(так как
![]() ).
По теореме Пифагора
).
По теореме Пифагора
![]() ,
,
![]() ,
а
,
а
![]() .
Теперь
.
Теперь
![]() ,
,
![]() и
и
![]() .
Отсюда находим объем нижней части
пирамиды:
.
Отсюда находим объем нижней части
пирамиды:
![]() и объем верхней части пирамиды:
и объем верхней части пирамиды:
![]() .
Следовательно,
.
Следовательно,
![]() - отношение
объемов рассекаемых плоскостью частей
пирамиды.
- отношение
объемов рассекаемых плоскостью частей
пирамиды.
Так
как объем пирамиды
![]() ,
где
,
где
![]() - расстояние
от вершины
- расстояние
от вершины
![]() до секущей плоскости,
то
до секущей плоскости,
то
![]() .
.
Наконец,
![]() - это линейный угол двухгранного угла,
образованного плоскостью основания
пирамиды и секущей плоскостью, и
- это линейный угол двухгранного угла,
образованного плоскостью основания
пирамиды и секущей плоскостью, и
![]() .
Поскольку
.
Поскольку
![]() ,
то
,
то
![]() .
Следовательно,
.
Следовательно,
![]() -
-
искомый угол между плоскостью основания и секущей плоскостью. #
Решить задачи:
14)
Угол между высотой правильной пирамиды
и ее боковым ребром равен
![]()
![]() .
В каком отношении делит высоту пирамиды
центр описанного около него шара?
.
В каком отношении делит высоту пирамиды
центр описанного около него шара?
15)
В основании
правильной четырехугольной пирамиды
лежит квадрат со стороной
![]() .
Высота пирамиды равна стороне этого
квадрата. Пирамида рассечена плоскостью,
параллельной ее боковой грани. Найти
периметр сечения, если известно, что в
него можно вписать окружность.
.
Высота пирамиды равна стороне этого
квадрата. Пирамида рассечена плоскостью,
параллельной ее боковой грани. Найти
периметр сечения, если известно, что в
него можно вписать окружность.
