Практикум по элементарной математике (цвет)

Таким образом, получаем ответ: . #

При каких значениях уравнение имеет единственное решение?

4) ; 5) ; 6) .

Для каких действительных чисел уравнение имеет 2 действительных решения?

7) ; 8) ; 9) .

Для каждого действительного числа решить систему уравнений:

10) 11) 12) 13)

14) 15)

Для каких действительных чисел система имеет два действительных решения?

16) 17) 18) 19)

27 задание

1) В первой части задания приведены задачи на количество корней заданного уравнения с параметром.

Пример 1. Для каких действительных чисел уравнение имеет 0, 1, 2, 3 или 4 действительных решений?

Решение. Перепишем уравнение в виде совокупности двух систем:

Пусть - дискриминант верхнего уравнения в совокупности двух систем, а и - его корни, и - дискриминант нижнего уравнения, а и - его корни. Рассмотрим теперь случаи, когда верхняя система в совокупности (а затем и нижняя) имеет 0, 1 и 2 решения.

1) Первая система имеет 0 решений, т.е. не имеет решений:

2) Первая система имеет 1 решение:

3) Первая система имеет 2 решения:

4) Вторая система имеет 0 решений:

5) Вторая система имеет 1 решение:

6) Вторая система имеет 2 решения:

Теперь уже легко ответить на поставленные в условии задачи вопросы.

А) Заданное уравнение имеет 0 решений, когда первая и вторая системы имеют по 0 решений:

Б) Заданное уравнение имеет 1 решение, когда первая система имеет 1 решение, а вторая система имеет 0 решений, и наоборот:

В) Заданное уравнение имеет 2 решения, когда первая и вторая системы имеют по 1 решению, или первая система имеет 2 решения, а вторая система имеет 0 решений, и наоборот:

.

Г) Заданное уравнение имеет 3 решения, когда первая система имеет 2 решения, а вторая система имеет 1 решение, и наоборот:

.

Д) Заданное уравнение имеет 4 решения, когда первая и вторая системы имеют по 2 решения:

. #

Для каких действительных чисел уравнение имеет 0, 1, 2, 3, 4 решения?

1) ; 2) ; 3) ;

4) ; 5) .

Для каких действительных чисел уравнение имеет на отрезке ровно корней?

6) , , ;

7) , , .

2) Во второй части задания приведены задачи на расположение корней двух уравнений с одинаковым параметром.

Найти все , при которых уравнения имеют по два различных действительных корня и между корнями одного уравнения содержится ровно один корень другого уравнения:

8) и ; 9) и .

Найти все , при которых уравнения имеют по два различных действительных корня и между корнями одного из уравнений нет ни одного корня другого уравнения:

10) и ; 11) и .

12) Для каких действительных чисел всякое решение неравенства больше любого решения неравенства ?

13) Найти все действительные числа , при каждом из которых любое решение неравенства является решением неравенства .

28 задание

Данное задание содержит задачи на неравенства с параметрами.

Пример 1. Для каждого действительного числа решить неравенство: .

Решение. Найдем сначала область определения неравенства:

.

Далее, учитывая, что корни уравнения - это , имеем:

Для каждого действительного числа решить неравенство:

1) ; 2) ; 3) ;

4) ; 5) ; 6) ;

7) ; 8) ; 9) ;

10) ; 11) ; 12) ; 13) ; 14) ;

15) ; 16) ; 17) ; 18) .

29 задание

1) В первой части задания содержатся различные задачи на неравенства с параметрами.

Пример 1. Найти все действительные числа , при каждом из которых неравенство выполняется для всех действительных чисел .

Решение. Преобразуем заданное неравенство:

и положим . Теперь исходная задача будет выглядеть следующим образом: найти все действительные числа , при каждом из которых неравенство выполняется для всех . Вычислим корни уравнения :

.

Задача сводится теперь к выполнению включения: , где и , т.е. к решению следующей системы неравенств:

Решим по отдельности каждое из неравенств системы:

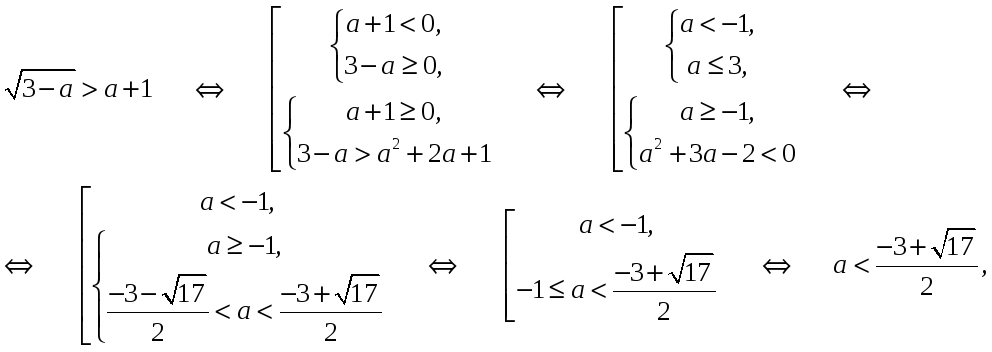
Таким образом, окончательно получаем:

Для каких действительных чисел (целых чисел ) неравенство верно для всех чисел :

1) ; 2) ; 3) ; 4) ; 5) ;

6) ; 7) .

Найти все действительные числа , при каждом из которых для всех выполняется неравенство:

8) , ; 9) , ;

10) , ; 11) , .

12) Найти все действительные числа , при каждом из которых любое решение неравенства является решением неравенства .

13) Найти все числа , при каждом из которых любое действительное число является решением хотя бы одного из неравенств: и .

2) Во второй части задания содержатся задачи на сечения кубов и призм плоскостями.

Пример 2. В каком отношении делит объем куба плоскость, проходящая через вершины , и точку , расположенную на ребре так, что ? Найдите площадь и периметр полученного сечения (длина ребра куба равна ), а также расстояние от точки до секущей плоскости и угол между плоскостью нижнего основания и секущей плоскостью.

Решение. Пусть - точка пересечения продолжения ребра с прямой .

Искомое сечение – это равнобедренная трапеция , образованная отсечением от равнобедренного его вершины отрезком , параллельным . Перейдем к необходимым вычислениям. Так как , то , откуда 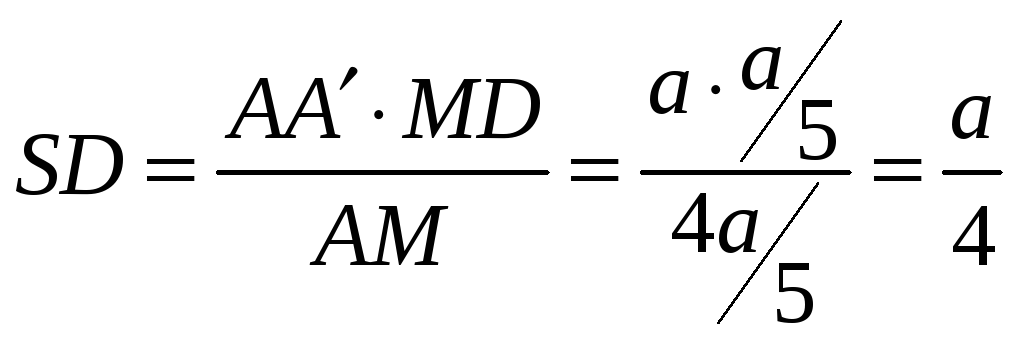. Следовательно, , и . Поскольку , то , и . Отсюда находим периметр сечения:

.

Далее заметим, что является высотой ( и ), поэтому . Теперь легко найти площадь сечения:

.

Далее вычислим объем пирамиды : . С другой стороны, если - перпендикуляр, опущенный из вершины куба на плоскость , то , поэтому можно найти расстояние от вершины до секущей плоскости:

.

Теперь найдем объем передней части куба :

и объем задней части куба: , откуда получаем отношение объмов двух частей, на которые делится куб секущей плоскостью:

.

Наконец, поскольку - это линейный угол двухгранного угла, образованного плоскостью нижнего основания куба и секущей плоскостью, а , то находим угол между плоскостью нижнего основания и секущей плоскостью:

. #

Решить задачи:

14) Дан куб с ребром, равным дм. На продолжении ребра за точку взята точка так, что дм. Через точку и середины ребер и проведена плоскость. Найдите периметр и площадь полученного сечения, а также расстояние от точки до секущей плоскости и угол между плоскостью верхнего основания и этой плоскостью. В каком отношении делит объем куба секущая плоскость?

15) В каком отношении делит объем куба плоскость, проходящая через вершину и середины ребер и ? Найдите площадь и периметр полученного сечения (длина ребра куба равна ), а также расстояние от точки до секущей плоскости и угол между плоскостью верхнего основания и этой плоскостью.

16) В каком отношении делит объем правильной треугольной призмы плоскость, проходящая через вершину и середины ребер и ? Найдите площадь и периметр сечения, если длины всех ребер призмы равны , а также расстояние от точки до секущей плоскости и угол между плоскостью нижнего основания и этой плоскостью.

17) Основание прямой призмы - равносторонний треугольник со стороной дм. На продолжении ребра за точку взята точка так, что дм. Через точку и середины ребер и проведена плоскость. Найдите периметр и площадь полученного сечения, если дм, а также расстояние от точки до секущей плоскости и угол между плоскостью нижнего основания и этой плоскостью. В каком отношении делит объем призмы секущая плоскость?

18) В прямоугольном параллелепипеде с ребрами см и см через вершины , и точку , лежащую на ребре , проведена плоскость. Какую наименьшую площадь может иметь сечение параллелепипеда этой плоскостью?

30 задание

1) В первой части задания содержатся различные задачи с параметрами.

Пример 1. Найти все числа , для каждого из которых система имеет действительные решения.